Корреляционная функция (статистическая механика)

Чтобы узнать о других значениях, см. Функция корреляции (значения) .

Схематические равновременные спиновые корреляционные функции для ферромагнетиков и антиферромагнетиков как сверху, так и снизу. $T_{\text{Curie}}$ от расстояния, нормированного на корреляционную длину, $\xi$. Во всех случаях корреляции наиболее сильны вблизи начала координат, что указывает на то, что спин оказывает наибольшее влияние на своих ближайших соседей. Все корреляции постепенно затухают по мере увеличения расстояния от спина в начале координат. Выше температуры Кюри корреляция между спинами стремится к нулю, поскольку расстояние между спинами становится очень большим. Напротив, ниже $T_{\text{Curie}}$, корреляция между спинами не стремится к нулю на больших расстояниях, а затухает до уровня, соответствующего дальнему порядку системы. Разница в поведении распада, когда корреляции между микроскопическими случайными величинами становятся нулевыми или ненулевыми на больших расстояниях, является одним из способов определения ближнего и дальнего порядка.

В статистической механике корреляционная функция является мерой порядка в системе, характеризуемой математической корреляционной функцией . Корреляционные функции описывают, как связаны микроскопические переменные, такие как спин и плотность, в разных положениях. Более конкретно, корреляционные функции количественно измеряют степень, в которой микроскопические переменные колеблются вместе в среднем в пространстве и/или времени. Имейте в виду, что корреляция не означает автоматически причинно-следственную связь. Таким образом, даже если между двумя точками пространства или времени существует ненулевая корреляция, это не означает, что между ними существует прямая причинно-следственная связь. Иногда корреляция может существовать без какой-либо причинно-следственной связи. Это может быть чисто случайно или связано с другими основными факторами, известными как мешающие переменные, которые приводят к ковариации обеих точек (статистически).

Классический пример пространственной корреляции можно увидеть в ферромагнитных и антиферромагнитных материалах. В этих материалах спины атомов имеют тенденцию располагаться параллельно и антипараллельно со своими соседними аналогами соответственно. Рисунок справа наглядно представляет эту пространственную корреляцию между спинами в таких материалах.

Определения

Наиболее распространенное определение корреляционной функции — это каноническое ансамблевое (тепловое) среднее скалярного произведения двух случайных величин: $s_{1}$ и $s_{2}$, на позициях $R$ и $R+r$ и время $t$ и $t+\tau$: $$C(r,\tau )=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t+\tau )\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t+\tau )\rangle \,.$$

Здесь скобки, $\langle \cdot \rangle$, указывают вышеупомянутое среднее тепловое значение. Однако здесь важно отметить, что, хотя скобки называются средними, они рассчитываются как ожидаемое значение , а не среднее значение. Вопрос о том, следует ли вычитать некоррелированный средний продукт $s_{1}$ и $s_{2}$, $\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t+\tau )\rangle$ из коррелированного продукта, $\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t+\tau )\rangle$, причем соглашение различается в зависимости от поля. Чаще всего корреляционные функции используются в тех случаях, когда $s_{1}$ и $s_{2}$ описывают одну и ту же переменную, например, корреляционную функцию спин-спин или корреляционную функцию положения частицы в элементарной жидкости или твердом теле (часто называемую функцией радиального распределения или парной корреляционной функцией). Корреляционные функции между одной и той же случайной величиной являются автокорреляционными функциями . Однако в статистической механике не все корреляционные функции являются автокорреляционными. Например, в многокомпонентных конденсированных фазах часто представляет интерес парная корреляционная функция между различными элементами. Такие парные корреляционные функции смешанных элементов являются примером функций взаимной корреляции , поскольку случайные величины $s_{1}$ и $s_{2}$ представляют средние изменения плотности как положение функции для двух различных элементов.

Равновесные равновременные (пространственные) корреляционные функции

Часто нас интересует исключительно пространственное влияние данной случайной величины, скажем, направления вращения, на ее локальное окружение, без учета более поздних моментов времени. $\tau$. В этом случае мы пренебрегаем эволюцией системы во времени, поэтому приведенное выше определение переписывается с помощью $\tau =0$. Это определяет равновременную корреляционную функцию , $C(r,0)$. Это написано как: $$C(r,0)=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t)\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t)\rangle \,.$$

Часто опорное время опускают, $t$, и опорный радиус, $R$, предполагая равновесие (и, следовательно, неизменность ансамбля во времени) и усредняя по всем положениям выборки, что дает: $$C(r)=\langle \mathbf {s_{1}} (0)\cdot \mathbf {s_{2}} (r)\rangle \ -\langle \mathbf {s_{1}} (0)\rangle \langle \mathbf {s_{2}} (r)\rangle$$где, опять же, выбор того, вычитать ли некоррелированные переменные, различается в зависимости от поля. Функция радиального распределения является примером равновременной корреляционной функции, в которой некоррелированная опорная величина обычно не вычитается. На этой странице показаны другие функции спин-спиновой корреляции за равное время для различных материалов и условий.

Равновесные равнопозиционные (временные) корреляционные функции

Также может быть интересна временная эволюция микроскопических переменных. Другими словами, как значение микроскопической переменной в данном положении и в данный момент времени $R$ и $t$, влияет на значение той же микроскопической переменной в более позднее время, $t+\tau$ (и обычно в одной и той же позиции). Такие временные корреляции количественно оцениваются с помощью корреляционных функций равного положения , $C(0,\tau )$. Они определяются аналогично приведенным выше функциям равновременной корреляции, но теперь мы пренебрегаем пространственными зависимостями, полагая $r=0$, что дает: $$C(0,\tau )=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R,t+\tau )\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R,t+\tau )\rangle \,.$$

Предполагая равновесие (и, следовательно, неизменность ансамбля во времени) и усреднение по всем участкам выборки дает более простое выражение для корреляционной функции равного положения, чем для корреляционной функции равного времени: $$C(\tau )=\langle \mathbf {s_{1}} (0)\cdot \mathbf {s_{2}} (\tau )\rangle \ -\langle \mathbf {s_{1}} (0)\rangle \langle \mathbf {s_{2}} (\tau )\rangle \,.$$

Вышеприведенное предположение на первый взгляд может показаться неинтуитивным: как ансамбль, инвариантный во времени, может иметь неоднородную временную корреляционную функцию? Временные корреляции остаются актуальными для разговоров в равновесных системах, поскольку неизменный во времени макроскопический ансамбль все еще может иметь нетривиальную временную динамику с микроскопической точки зрения . Одним из примеров является диффузия. Однофазная система в равновесии имеет макроскопически однородный состав. Однако если наблюдать за микроскопическим движением каждого атома, то можно заметить, что постоянно происходят колебания состава из-за квазислучайных блужданий отдельных атомов. Статистическая механика позволяет делать глубокие утверждения о временном поведении таких колебаний равновесных систем. Это обсуждается ниже в разделе, посвященном временной эволюции корреляционных функций и гипотезе регрессии Онзагера .

Обобщение за пределами равновесных корреляционных функций

Все вышеперечисленные корреляционные функции были определены в контексте равновесной статистической механики. Однако можно определить корреляционные функции для систем, находящихся вдали от равновесия. Рассмотрев общее определение $C(r,\tau )$, ясно, что можно определить случайные величины, используемые в этих корреляционных функциях, такие как положения атомов и спины, вдали от равновесия. Таким образом, их скалярное произведение четко определено вдали от равновесия. Операция, которая больше не четко определена вдали от равновесия, представляет собой усреднение по равновесному ансамблю. Этот процесс усреднения для неравновесной системы обычно заменяется усреднением скалярного произведения по всей выборке. Это типично для экспериментов по рассеянию и компьютерного моделирования и часто используется для измерения функций радиального распределения стекол.

Можно также определить средние значения по состояниям для систем, слегка отклоненных от равновесия. См., например, http://xbeams.chem.yale.edu/~batista/vaa/node56.html. Архивировано 25 декабря 2018 г. на Wayback Machine.

Измерение корреляционных функций

Корреляционные функции обычно измеряются с помощью экспериментов по рассеянию. Например, эксперименты по рассеянию рентгеновских лучей напрямую измеряют электрон-электронные равновременные корреляции. Зная факторы элементной структуры, можно также измерить корреляционные функции пар элементов. см. в разделе «Функция радиального распределения» Дополнительную информацию . Равновременные спин-спиновые корреляционные функции измеряются с помощью рассеяния нейтронов , а не рассеяния рентгеновских лучей. Рассеяние нейтронов также может дать информацию о парных корреляциях. Для систем, состоящих из частиц размером более одного микрометра, оптическая микроскопия может использоваться для измерения как равновременных, так и равнопозиционных корреляционных функций. Таким образом, оптическая микроскопия распространена для коллоидных суспензий, особенно в двух измерениях.

Эволюция корреляционных функций во времени

В 1931 году Ларс Онсагер предположил, что регрессия микроскопических тепловых флуктуаций в состоянии равновесия следует макроскопическому закону релаксации малых неравновесных возмущений. Это известно как гипотеза регрессии Онзагера . Поскольку значения микроскопических переменных разделены большими временными масштабами, $\tau$, не должна быть коррелирована за пределами того, что мы ожидаем от термодинамического равновесия, эволюцию во времени корреляционной функции можно рассматривать с физической точки зрения, как систему, постепенно «забывающую» начальные условия, наложенные на нее посредством указания некоторой микроскопической переменной. Действительно, существует интуитивная связь между временной эволюцией корреляционных функций и временной эволюцией макроскопических систем: в среднем корреляционная функция развивается во времени так же, как если бы система была подготовлена ​​в условиях, заданных начальным значением корреляционной функции. и дали возможность развиваться.

Равновесные колебания системы можно связать с ее реакцией на внешние возмущения посредством теоремы о флуктуации-диссипации .

Связь между фазовыми переходами и корреляционными функциями

Равновременные корреляционные функции, $C(r,\tau =0)$, как функция радиуса для ферромагнитной спиновой системы выше, при и ниже критической температуры, $T_{C}$. Выше $T_{C}$, $C(r,\tau =0)$ демонстрирует комбинированную экспоненциальную и степенную зависимость от расстояния: $C(r,\tau =0)\propto r^{-\vartheta }e^{-r/\xi (T)}$. Степенная зависимость доминирует на расстояниях, малых по отношению к корреляционной длине, $\xi$, а экспоненциальная зависимость доминирует на расстояниях, больших относительно $\xi$. В $T_{C}$, корреляционная длина расходится, $\xi (T_{C})=\infty$, что приводит к исключительно степенному поведению: $C(r,\tau =0)\propto r^{-(d-2+\eta )}$. $T_{C}$ отличается крайней нелокальностью пространственных корреляций между микроскопическими значениями соответствующего параметра порядка без дальнего порядка. Ниже $T_{C}$, спины обладают спонтанным упорядочением, т.е. дальним порядком, и бесконечной корреляционной длиной. Непрерывные переходы порядок-беспорядок можно понимать как процесс корреляционной длины, $\xi$, переходя от бесконечности в низкотемпературном упорядоченном состоянии к бесконечности в критической точке, а затем к конечности в высокотемпературном неупорядоченном состоянии.

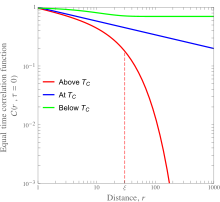
Непрерывные фазовые переходы, такие как переходы порядок-беспорядок в металлических сплавах и переходы ферромагнит-парамагнитный, связаны с переходом из упорядоченного состояния в неупорядоченное. С точки зрения корреляционных функций, равновременная корреляционная функция отлична от нуля для всех точек решетки ниже критической температуры и не пренебрежимо мала только для довольно небольшого радиуса выше критической температуры. Поскольку фазовый переход является непрерывным, длина, на которой коррелируют микроскопические переменные, $\xi$, должен непрерывно переходить от бесконечности к конечной, когда материал нагревается до критической температуры. Это приводит к степенной зависимости корреляционной функции от расстояния в критической точке. Это показано на рисунке слева для случая ферромагнитного материала, количественные подробности указаны в разделе, посвященном магнетизму.

Приложения

Магнетизм

В спиновой системе особенно хорошо изучена равновременная корреляционная функция. Он описывает каноническое ансамблевое (тепловое) среднее скалярного произведения спинов в двух точках решетки по всем возможным порядкам: $C(r)=\langle \mathbf {s} (R)\cdot \mathbf {s} (R+r)\rangle \ -\langle \mathbf {s} (R)\rangle \langle \mathbf {s} (R+r)\rangle \,.$Здесь скобки означают упомянутое выше тепловое среднее значение. Схематические графики этой функции показаны для ферромагнитного материала ниже, при и выше температуры Кюри слева.

Даже в магнитно-неупорядоченной фазе спины в разных положениях коррелированы, т. е. если расстояние r очень мало (по сравнению с некоторым масштабом длины $\xi$), взаимодействие между спинами приведет к их корреляции.Выравнивание, которое естественным образом возникло бы в результате взаимодействия спинов, разрушается тепловыми эффектами. При высоких температурах с увеличением расстояния наблюдаются экспоненциально затухающие корреляции, причем корреляционная функция асимптотически определяется выражением

$C(r)\approx {\frac {1}{r^{\vartheta }}}\exp {\left(-{\frac {r}{d}}\right)}\,,$

где r — расстояние между спинами, d — размерность системы, а $\vartheta$ представляет собой показатель степени, значение которого зависит от того, находится ли система в неупорядоченной фазе (т.е. выше критической точки) или в упорядоченной фазе (т.е. ниже критической точки). При высоких температурах корреляция спадает до нуля экспоненциально с увеличением расстояния между спинами. Такой же экспоненциальный затух в зависимости от радиального расстояния наблюдается и ниже. $T_{c}$, но пределом на больших расстояниях является средняя намагниченность $\langle M^{2}\rangle$. Именно в критической точке наблюдается алгебраическое поведение.

$C(r)\approx {\frac {1}{r^{(d-2+\eta )}}}\,,$

где $\eta$ является критическим показателем , который не имеет простой связи с некритическим показателем $\vartheta$ представлено выше. Например, точное решение двумерной модели Изинга (с короткодействующими ферромагнитными взаимодействиями) дает именно при критичности $\eta ={\frac {1}{4}}$, но выше критичности $\vartheta ={\frac {1}{2}}$ и ниже критичности $\vartheta =2$.

При понижении температуры тепловое разупорядочение уменьшается, а при непрерывном фазовом переходе корреляционная длина расходится, так как корреляционная длина должна непрерывно переходить от конечного значения выше фазового перехода к бесконечному ниже фазового перехода:

$\xi \propto |T-T_{c}|^{-\nu }\,,$

с другим критическим показателем $\nu$.

Эта степенная корреляция отвечает за масштабирование , наблюдаемое при этих переходах. Все упомянутые показатели степени не зависят от температуры.На самом деле они универсальны , то есть одинаковы в самых разных системах.

Функции радиального распределения

Одной из общих корреляционных функций является функция радиального распределения , которая часто встречается в статистической механике и механике жидкости . Корреляционная функция может быть рассчитана в точно решаемых моделях (одномерный бозе-газ, спиновые цепочки, модель Хаббарда) с помощью квантового метода обратной задачи рассеяния и анзаца Бете . В изотропной XY-модели временные и температурные корреляции оценивали Итс, Корепин, Изергин и Славнов.

Корреляционные функции высшего порядка

Корреляционные функции более высокого порядка включают в себя несколько контрольных точек и определяются посредством обобщения вышеуказанной корреляционной функции путем принятия ожидаемого значения произведения более чем двух случайных величин:

$C_{i_{1}i_{2}\cdots i_{n}}(s_{1},s_{2},\cdots ,s_{n})=\langle X_{i_{1}}(s_{1})X_{i_{2}}(s_{2})\cdots X_{i_{n}}(s_{n})\rangle .$

Однако такие корреляционные функции более высокого порядка относительно сложно интерпретировать и измерять. Например, для измерения аналогов парных функций распределения высших порядков необходимы источники когерентного рентгеновского излучения. Обе теории такого анализа и экспериментальное измерение необходимых рентгеновских кросскорреляционных функций являются областями активных исследований.

См. также

• Уравнение Орнштейна – Цернике

Дальнейшее чтение

• Сетна, Джеймс П. (2006). «Глава 10: Корреляции, реакция и рассеивание». Статистическая механика: энтропия, параметры порядка и сложность . Издательство Оксфордского университета. ISBN  978-0198566779 .
• Функция радиального распределения
• Йоманс, Дж. М. (1992). Статистическая механика фазовых переходов . Оксфордские научные публикации. ISBN  978-0-19-851730-6 .
• Фишер, Мэн (1974). «Ренормгруппа в теории критического поведения». Обзоры современной физики . 46 (4): 597–616. Бибкод : 1974РвМП...46..597Ф . дои : 10.1103/RevModPhys.46.597 .
• К. Домб , М. С. Грин , Дж. Л. Лебовица редакторы , Фазовые переходы и критические явления , том. 1-20 (1972–2001), Академик Пресс.