Классическая модель XY

Классическая модель XY (иногда также называемая ротора ( ротатора ) классической моделью или моделью O(2) ) — это решетчатая модель статистической механики . В общем, модель XY можно рассматривать как специализацию n -векторной модели Стэнли. для n = 2 .

Определение

Учитывая D -мерную решетку Λ , на каждый узел решетки j ∈ Λ существует двумерный вектор единичной длины s _j = (cos θ _j , sin θ _j )

s Спиновая конфигурация ( = s j ₎ j _{∈ Λ} является назначением угла − π < θ _j ≤ π для каждого j ∈ Λ .

Учитывая трансляционно-инвариантное взаимодействие J _ij = J ( i − j ) и точечно-зависимое внешнее поле $\mathbf {h} _{j}=(h_{j},0)$, энергия конфигурации равна

$H(\mathbf {s} )=-\sum _{i\neq j}J_{ij}\;\mathbf {s} _{i}\cdot \mathbf {s} _{j}-\sum _{j}\mathbf {h} _{j}\cdot \mathbf {s} _{j}=-\sum _{i\neq j}J_{ij}\;\cos(\theta _{i}-\theta _{j})-\sum _{j}h_{j}\cos \theta _{j}$

Случай, в котором J _ij = 0, за исключением ближайшего соседа ij, называется случаем ближайшего соседа .

Вероятность конфигурации определяется распределением Больцмана с обратной температурой β ≥ 0 :

$P(\mathbf {s} )={\frac {e^{-\beta H(\mathbf {s} )}}{Z}}\qquad Z=\int _{[-\pi ,\pi ]^{\Lambda }}\prod _{j\in \Lambda }d\theta _{j}\;e^{-\beta H(\mathbf {s} )}.$

где Z — нормализация или статистическая сумма . Обозначения $\langle A(\mathbf {s} )\rangle$ указывает математическое ожидание случайной величины A ( s ) в пределе бесконечного объема после периодических граничных условий наложения .

Точные результаты

• Существование термодинамического предела для свободной энергии и спиновых корреляций доказал Жинибре , распространив на этот случай неравенство Гриффитса .
• Использование неравенства Гриффитса в формулировке Джинибре, Айзенмана и Саймона что двухточечная спиновая корреляция модели ферромагнетика XY в измерении D , связь J > 0 и обратная температура β доминирует доказал , (т.е. имеет верхнюю границу, заданную) двухточечной корреляцией ферромагнитной модели Изинга в измерении D , связь J > 0 и обратная температура ⁠ β / 2 ⁠ $$\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle _{J,2\beta }\leq \langle \sigma _{i}\sigma _{j}\rangle _{J,\beta }$$ Следовательно, критическая β модели XY не может быть меньше двойной критической температуры модели Изинга. $$\beta _{c}^{XY}\geq 2\beta _{c}^{\rm {Is}}$$

Одно измерение

«ближайшего соседа» Как и в любой n -векторной модели со свободными (непериодическими) граничными условиями, если внешнее поле равно нулю, существует простое точное решение. В случае свободных граничных условий гамильтониан имеет вид $$H(\mathbf {s} )=-J[\cos(\theta _{1}-\theta _{2})+\cdots +\cos(\theta _{L-1}-\theta _{L})]$$следовательно, статистическая сумма факторизуется при изменении координат $$\theta _{j}=\theta _{j}'+\theta _{j-1}\qquad j\geq 2$$Это дает $${\begin{aligned}Z&=\int _{-\pi }^{\pi }d\theta _{1}\cdots d\theta _{L}\;e^{\beta J\cos(\theta _{1}-\theta _{2})}\cdots e^{\beta J\cos(\theta _{L-1}-\theta _{L})}\\&=2\pi \prod _{j=2}^{L}\int _{-\pi }^{\pi }d\theta '_{j}\;e^{\beta J\cos \theta '_{j}}=(2\pi )\left[\int _{-\pi }^{\pi }d\theta '_{j}\;e^{\beta J\cos \theta '_{j}}\right]^{L-1}=(2\pi )^{L}(I_{0}(\beta J))^{L-1}\end{aligned}}$$где $I_{0}$ — модифицированная функция Бесселя первого рода. Статистическая сумма может использоваться для нахождения нескольких важных термодинамических величин. Например, в термодинамическом пределе ( $L\to \infty$), свободная энергия на спин равна $$f(\beta ,h=0)=-\lim _{L\to \infty }{\frac {1}{\beta L}}\ln Z=-{\frac {1}{\beta }}\ln[2\pi I_{0}(\beta J)]$$Используя свойства модифицированных функций Бесселя, удельную теплоемкость (на спин) можно выразить как $${\frac {c}{k_{\rm {B}}}}=\lim _{L\to \infty }{\frac {1}{L(k_{\rm {B}}T)^{2}}}{\frac {\partial ^{2}}{\partial \beta ^{2}}}(\ln Z)=K^{2}\left(1-{\frac {\mu }{K}}-\mu ^{2}\right)$$где $K=J/k_{\rm {B}}T$, и $\mu$ – короткодействующая корреляционная функция,

Точная удельная теплоемкость на спин в одномерной модели XY

$$\mu (K)=\langle \cos(\theta -\theta ')\rangle ={\frac {I_{1}(K)}{I_{0}(K)}}$$

Даже в термодинамическом пределе разницы в теплоемкости нет. Действительно, как и одномерная модель Изинга, одномерная модель XY не имеет фазовых переходов при конечной температуре.

То же вычисление для периодического граничного условия (и при этом h = 0 ) требует формализма матрицы переноса , хотя результат тот же.

показывать

(Нажмите «показать» справа, чтобы увидеть детали формализма матрицы переноса.)

The partition function can be evaluated as $$Z={\text{tr}}\left\{\prod _{i=1}^{N}\oint d\theta _{i}e^{\beta J\cos(\theta _{i}-\theta _{i+1})}\right\}$$which can be treated as the trace of a matrix, namely a product of matrices (scalars, in this case). The trace of a matrix is simply the sum of its eigenvalues, and in the thermodynamic limit $L\to \infty$ only the largest eigenvalue will survive, so the partition function can be written as a repeated product of this maximal eigenvalue. This requires solving the eigenvalue problem$$\oint d\theta '\exp\{\beta J\cos(\theta '-\theta )\}\psi (\theta ')=z_{i}\psi (\theta )$$Note the expansion $$\exp\{\beta J\cos(\theta -\theta ')\}=\sum _{n=-\infty }^{\infty }I_{n}(\beta J)e^{in(\theta -\theta ')}=\sum _{n=-\infty }^{\infty }\omega _{n}\psi _{n}^{*}(\theta ')\psi _{n}(\theta )$$

which represents a diagonal matrix representation in the basis of its plane-wave eigenfunctions $\psi =\exp(in\theta )$. The eigenvalues of the matrix is simply are modified Bessel functions evaluated at $\beta J$, namely $\omega _{n}=2\pi I_{n}(\beta J)$. For any particular value of $\beta J$, these modified Bessel functions satisfy $I_{0}>I_{1}>I_{2}>\cdots$ and $I_{-n}(\beta J)=I_{n}(\beta J)$. Therefore in the thermodynamic limit the eigenvalue $I_{0}$ will dominate the trace, and so $Z=[2\pi I_{0}(\beta J)]^{L}$.

Этот подход матрицы переноса также необходим при использовании свободных граничных условий, но с приложенным полем. $h\neq 0$. Если прикладное поле $h$ достаточно мала, чтобы ее можно было рассматривать как возмущение системы в нулевом поле, тогда магнитная восприимчивость $\chi \equiv \partial M/\partial h$ можно оценить. Это делается путем использования собственных состояний, вычисленных с помощью подхода матрицы переноса, и вычисления энергетического сдвига с помощью теории возмущений второго порядка , а затем сравнения с разложением по свободной энергии. $F=F_{0}-{\frac {1}{2}}\chi h^{2}$. Можно найти $$\chi (h\to 0)={\frac {C}{T}}{\frac {1+\mu }{1-\mu }}$$где $C$ — константа Кюри (значение, обычно связанное с восприимчивостью магнитных материалов). Это выражение справедливо и для одномерной модели Изинга с заменой $\mu =\tanh K$.

Два измерения

Среднеквадратичная магнетизация для решетки 25х25 (Ота: 30x30), что предполагает увеличение магнитного момента, которого нет в термодинамическом пределе.

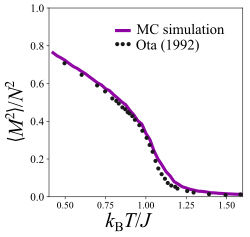
Двумерная модель XY с взаимодействиями ближайших соседей является примером двумерной системы с непрерывной симметрией, которая не имеет дальнего порядка, как того требует теорема Мермина-Вагнера . Точно так же не существует обычного фазового перехода , который был бы связан с нарушением симметрии . Однако, как будет обсуждаться позже, в системе действительно наблюдаются признаки перехода из неупорядоченного высокотемпературного состояния в квазиупорядоченное состояние ниже некоторой критической температуры, называемое переходом Костерлица-Таулсса . В случае дискретной решетки спинов двумерную модель XY можно оценить с использованием подхода матрицы переноса, сводя модель к проблеме собственных значений и используя наибольшее собственное значение из матрицы переноса. Хотя точное решение трудно найти, можно использовать определенные приближения для получения оценок критической температуры. $T_{c}$ что происходит при низких температурах. Например, Мэттис (1984 г.) ) использовал приближение к этой модели для оценки критической температуры системы как $$(2k_{\rm {B}}T_{c}/J)\ln(2k_{\rm {B}}T_{c}/J)=1$$$$k_{\rm {B}}T_{c}/J\approx 0.8816$$ Модель 2D XY также была очень подробно изучена с использованием моделирования Монте-Карло , например, с помощью алгоритма Метрополиса . Их можно использовать для расчета термодинамических величин, таких как энергия системы, удельная теплоемкость, намагниченность и т. д., в диапазоне температур и временных масштабов. В моделировании Монте-Карло каждому вращению соответствует постоянно меняющийся угол. $\theta _{i}$ (часто его можно разбить на конечное число углов, как в связанной модели Поттса , для простоты вычислений. Однако это не является обязательным требованием.) На каждом временном шаге алгоритм Метрополиса выбирает один спин случайным образом и поворачивает его угол с каким-то случайным приращением $\Delta \theta _{i}\in (-\Delta ,\Delta )$. Изменение угла приводит к изменению энергии $\Delta E_{i}$ системы, которая может быть положительной или отрицательной. Если отрицательно, алгоритм принимает изменение угла; если положительный, конфигурация принимается с вероятностью $e^{-\beta \Delta E_{i}}$, фактор Больцмана для изменения энергии. Метод Монте-Карло использовался для проверки различными методами критической температуры системы и, по оценкам, составляет $k_{\rm {B}}T_{c}/J=0.8935(1)$. Метод Монте-Карло также позволяет вычислять средние значения, которые используются для расчета термодинамических величин, таких как намагниченность, спин-спиновая корреляция, корреляционные длины и теплоемкость. Это важные способы охарактеризовать поведение системы вблизи критической температуры. Например, намагниченность и квадрат намагниченности можно вычислить как

Удельная теплоемкость двумерной модели XY, рассчитанная методом Монте-Карло на квадратных решетках размером до 4096 x 4096 (Нгуен: ), показывая функцию на $k_{\rm {B}}T/J\approx 1.167$, над переходом КТ . На вставке показано положение пика в зависимости от размера решетки.

$${\frac {\langle M\rangle }{N}}={\frac {1}{N}}|\langle \mathbf {s} \rangle |={\frac {1}{N}}\left|\left\langle \left(\sum _{i=1}^{N}\cos \theta _{i},\sum _{i=1}^{N}\sin \theta _{i}\right)\right\rangle \right|$$$${\frac {\langle M^{2}\rangle }{N^{2}}}={\frac {1}{N^{2}}}\left\langle s_{x}^{2}+s_{y}^{2}\right\rangle ={\frac {1}{N^{2}}}\left\langle \left(\sum _{i=1}^{N}\cos \theta _{i}\right)^{2}+\left(\sum _{i=1}^{N}\sin \theta _{i}\right)^{2}\right\rangle$$где $N=L\times L$ это количество вращений. Средняя намагниченность характеризует величину чистого магнитного момента системы; во многих магнитных системах оно равно нулю выше критической температуры и самопроизвольно становится отличным от нуля при низких температурах. Аналогичным образом среднеквадратическая намагниченность характеризует среднее значение квадрата чистых компонентов спинов по всей решетке. Любой из них обычно используется для характеристики параметра порядка системы. Строгий анализ модели XY показывает, что намагниченность в термодинамическом пределе равна нулю, и что квадрат намагниченности примерно соответствует $\langle M^{2}\rangle \approx N^{-T/4\pi }$, который исчезает в термодинамическом пределе. Действительно, при высоких температурах эта величина приближается к нулю, поскольку компоненты спинов будут иметь тенденцию к хаотизации и, таким образом, в сумме равняться нулю. Однако при низких температурах для конечной системы среднеквадратическая намагниченность увеличивается, что позволяет предположить, что существуют области спинового пространства, которые выровнены и вносят вклад в ненулевой вклад. Показанная намагниченность (для решетки 25x25) является одним из примеров этого, который, по-видимому, предполагает фазовый переход, хотя в термодинамическом пределе такой переход не существует.

Более того, используя статистическую механику, можно связать термодинамические средние значения с такими величинами, как удельная теплоемкость, путем расчета $$c/k_{\rm {B}}={\frac {\langle E^{2}\rangle -\langle E\rangle ^{2}}{N(k_{\rm {B}}T)^{2}}}$$Удельная теплоемкость показана при низких температурах вблизи критической температуры. $k_{\rm {B}}T_{c}/J\approx 0.88$. При этой предсказанной температуре в теплоемкости нет никаких особенностей, соответствующих критическому поведению (например, расхождению). Действительно, оценка критической температуры происходит с помощью других методов, таких как модуль спиральности или температурная зависимость дивергенции восприимчивости. Однако в теплоемкости имеется особенность в виде пика при $1.167(1)k_{\rm {B}}T/J$. Было показано, что это положение и высота пика не зависят от размера системы для решеток с линейным размером более 256; действительно, аномалия теплоемкости остается округлой и конечной при увеличении размера решетки без расходящегося пика.

Природу критических переходов и вихреобразования можно выяснить, рассмотрев непрерывную версию XY-модели. Здесь дискретные спины $\theta _{n}$ заменяются полем $\theta ({\textbf {x}})$ представляющий угол вращения в любой точке пространства. В этом случае угол вращения $\theta ({\textbf {x}})$ должны плавно меняться при изменении положения. Разлагая исходный косинус в ряд Тейлора , гамильтониан можно выразить в континуальном приближении как $$E=\int {\frac {J}{2}}(\nabla \theta )^{2}\,d^{2}\mathbf {x}$$

Карта цветов (дискретной) двумерной модели XY в решетке 250x250 при $k_{\rm {B}}T/J=0.4$. Каждый спин представлен цветом, который соответствует углу между $(-\pi ,\pi ]$

Непрерывная версия модели XY часто используется для моделирования систем, которые обладают параметрами порядка с одинаковыми видами симметрии, например, сверхтекучий гелий , гексатические жидкие кристаллы . Именно это отличает их от других фазовых переходов, всегда сопровождающихся нарушением симметрии. Топологические дефекты в XY-модели приводят к раскрепощающему вихрь переходу из низкотемпературной фазы в высокотемпературную неупорядоченную фазу . Действительно, тот факт, что при высоких температурах корреляции затухают экспоненциально быстро, а при низких температурах затухают по степенному закону, хотя в обоих режимах M ( β ) = 0 , называется переходом Костерлица–Таулесса . Костерлиц и Таулесс привели простой аргумент, объясняющий, почему это так: основное состояние рассматривается как состоящее из всех спинов одинаковой ориентации с добавлением одного вихря. Их присутствие увеличивает энтропию примерно $\Delta S=k_{\rm {B}}\ln(L^{2}/a^{2})$, где $a$ – эффективный масштаб длины (например, размер решетки для дискретной решетки). При этом энергия системы увеличивается за счет вихря на величину $\Delta E=\pi J\ln(L/a)$. Если сложить все это вместе, то свободная энергия системы изменится из-за спонтанного образования вихря на величину $$\Delta F=\Delta E-T\Delta S=(\pi J-2k_{\rm {B}}T)\ln(L/a)$$В термодинамическом пределе система не способствует образованию вихрей при низких температурах, но благоприятствует им при высоких температурах, выше критической температуры. $T_{c}=\pi J/2k_{\rm {B}}$. Это указывает на то, что при низких температурах любые возникающие вихри будут стремиться аннигилировать с антивихрями, чтобы снизить энергию системы. Действительно, качественно это будет так, если наблюдать «снимки» спиновой системы при низких температурах, когда вихри и антивихри постепенно объединяются, чтобы аннигилировать. Таким образом, низкотемпературное состояние будет состоять из связанных пар вихрь-антивихрь. Между тем, при высоких температурах будет существовать совокупность несвязанных вихрей и антивихрей, которые смогут свободно перемещаться по плоскости.

Чтобы визуализировать модель Изинга, можно использовать стрелку, направленную вверх или вниз или представленную в виде точки, окрашенной в черный/белый цвет, чтобы указать ее состояние. Чтобы визуализировать систему вращения XY, вращения можно представить в виде стрелки, указывающей в определенном направлении, или в виде точки определенного цвета. Здесь необходимо представить спин спектром цветов, обусловленным каждой из возможных непрерывных переменных. Это можно сделать, используя, например, непрерывный и периодический красно-зелено-синий спектр. Как показано на рисунке, голубой соответствует нулевому углу (указан вправо), тогда как красный соответствует углу в 180 градусов (направлен влево). Затем можно изучить снимки спиновых конфигураций при разных температурах, чтобы выяснить, что происходит выше и ниже критической температуры модели XY. При высоких температурах спины не будут иметь выделенной ориентации и произойдет непредсказуемое изменение углов между соседними спинами, так как не будет выделенной энергетически выгодной конфигурации. В этом случае карта цветов будет выглядеть сильно пиксельной. Между тем, при низких температурах в одной из возможных конфигураций основного состояния все спины направлены в одну и ту же ориентацию (один и тот же угол); они будут соответствовать областям (областям) цветовой карты, где все спины имеют примерно одинаковый цвет.

Различные формы вихрей и антивихрей, показанные в моделировании Монте-Карло в $k_{\rm {B}}T/J=0.4$

Чтобы идентифицировать вихри (или антивихри), возникшие в результате перехода Костерлица – Таулеса, можно определить изменение знака угла, пересекая круг точек решетки против часовой стрелки. Если общее изменение угла равно нулю, это соответствует отсутствию вихря; тогда как полное изменение угла $\pm 2\pi$ соответствует вихрю (или антивихрю). Эти вихри представляют собой топологически нетривиальные объекты, образующие пары вихрь-антивихрь, которые могут разделяться или попарно аннигилировать. На карте цветов эти дефекты можно обнаружить в областях с большим цветовым градиентом, где все цвета спектра встречаются вокруг одной точки. Качественно эти дефекты могут выглядеть как источники потока, направленные внутрь или наружу, или вихри вращений, которые вместе вращаются по часовой стрелке или против часовой стрелки, или гиперболические элементы, в которых некоторые спины направлены в сторону дефекта, а некоторые — в сторону от дефекта. Поскольку конфигурация изучается в длительных временных масштабах и при низких температурах, наблюдается, что многие из этих пар вихрь-антивихрь сближаются и в конечном итоге аннигилируют. Только при высоких температурах эти вихри и антивихри освобождаются и отделяются друг от друга.

В непрерывной модели XY исчезает высокотемпературная спонтанная намагниченность: $$M(\beta ):=|\langle \mathbf {s} _{i}\rangle |=0$$Кроме того, расширение кластера показывает, что спиновые корреляции кластеризуются экспоненциально быстро: например $$|\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\leq C(\beta )e^{-c(\beta )|i-j|}$$При низких температурах, т. е. β ≫ 1 , спонтанная намагниченность остается равной нулю (см. теорему Мермина–Вагнера ), $$M(\beta ):=|\langle \mathbf {s} _{i}\rangle |=0$$но затухание корреляций является лишь степенным законом: Фрелих и Спенсер нашел нижнюю границу

$|\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\geq {\frac {C(\beta )}{1+|i-j|^{\eta (\beta )}}}$

в то время как МакБрайан и Спенсер нашли верхнюю границу для любого $\epsilon >0$

$|\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\leq {\frac {C(\beta ,\epsilon )}{1+|i-j|^{\eta (\beta ,\epsilon )}}}$

Три и более измерений

Независимо от области взаимодействия, при достаточно низкой температуре намагниченность положительна.

• При высокой температуре спонтанная намагниченность исчезает: $M(\beta ):=|\langle \mathbf {s} _{i}\rangle |=0$. Кроме того, расширение кластера показывает, что спиновые корреляции кластеризуются экспоненциально быстро: например $|\langle \mathbf {s} _{i}\cdot \mathbf {s} _{j}\rangle |\leq C(\beta )e^{-c(\beta )|i-j|}$.
• При низкой температуре инфракрасный анализ показывает, что спонтанная намагниченность строго положительна: $M(\beta ):=|\langle \mathbf {s} _{i}\rangle |>0$. Кроме того, существует однопараметрическое семейство экстремальных состояний: $\langle \;\cdot \;\rangle ^{\theta }$, такой, что $\langle \mathbf {s} _{i}\rangle ^{\theta }=M(\beta )(\cos \theta ,\sin \theta )$ но, предположительно, в каждом из этих экстремальных состояний усеченные корреляции алгебраически затухают.

Фазовый переход

Как упоминалось выше, в одном измерении модель XY не имеет фазового перехода, а в двух измерениях имеет переход Березинского-Костерлица-Таулесса между фазами с экспоненциально и степенным затуханием корреляционных функций.

В трехмерном и более высоком измерениях модель XY имеет фазовый переход ферромагнетик-парамагнетик. При низких температурах спонтанная намагниченность отлична от нуля: это ферромагнитная фаза. С повышением температуры спонтанная намагниченность постепенно уменьшается и исчезает при критической температуре. Оно остается нулевым при всех более высоких температурах: это парамагнитная фаза.

В четырех и более измерениях фазовый переход имеет средние по теории поля критические показатели (с логарифмическими поправками в четырех измерениях).

Трехмерный случай: критические показатели

Трехмерный случай интересен тем, что критические показатели при фазовом переходе нетривиальны. Многие трехмерные физические системы принадлежат к тому же классу универсальности, что и трехмерная модель XY, и имеют одни и те же критические показатели, в первую очередь магниты легкой плоскости и жидкий гелий-4 . Значения этих критических показателей измеряются с помощью экспериментов, моделирования Монте-Карло, а также могут быть вычислены с помощью теоретических методов квантовой теории поля, таких как ренормгруппа и конформный бутстрап . Методы ренормгруппы применимы, поскольку считается, что критическая точка модели XY описывается фиксированной точкой ренормгруппы. Методы конформного бутстрапа применимы, поскольку также считается, что это унитарная трехмерная конформная теория поля .

Наиболее важные критические показатели трехмерной модели XY: $\alpha ,\beta ,\gamma ,\delta ,\nu ,\eta$. Все они могут быть выражены всего двумя числами: масштабными размерами. $\Delta _{\phi }$ и $\Delta _{s}$ поля комплексного параметра порядка $\phi$ и ведущего синглетного оператора $s$ (то же самое, что $|\phi |^{2}$ в описании Гинзбурга–Ландау ). Еще одним важным полем является $s'$(то же самое, что $|\phi |^{4}$), размерность которого $\Delta _{s'}$ определяет показатель поправки к масштабированию $\omega$. Согласно конформному бутстреп-вычислению, эти три измерения определяются следующим образом:

$\Delta _{\phi }$	0.519088(22)
$\Delta _{s}$	1.51136(22)
$\Delta _{s'}$	3.794(8)

Это дает следующие значения критических показателей:

	общее выражение ( $d=3$)	числовое значение
а	$2-d/(d-\Delta _{s})$	-0.01526(30)
б	$\Delta _{\phi }/(d-\Delta _{s})$	0.34869(7)
с	$(d-2\Delta _{\phi })/(d-\Delta _{s})$	1.3179(2)
д	$(d-\Delta _{\phi })/\Delta _{\phi }$	4.77937(25)
или	$2\Delta _{\phi }-d+2$	0.038176(44)
н	$1/(d-\Delta _{s})$	0.67175(10)
ой	$\Delta _{s'}-d$	0.794(8)

Методы Монте-Карло дают совместимые определения: $\eta =0.03810(8),\nu =0.67169(7),\omega =0.789(4)$.

См. также

• Классическая модель Гейзенберга
• Кулоновский газ
• Голдстоун бозон
• Модель Изинга
• Модель Поттса
• n -векторная модель
• Переход Костерлица – Таулесса
• Топологический дефект
• Сверхтекучая пленка
• Модель Сигмы
• Модель Синус-Гордон

Ссылки

• Евгений Демидов, Вихри в XY-модели (2004)

Дальнейшее чтение

• Х. Э. Стэнли, Введение в фазовые переходы и критические явления (Oxford University Press, Оксфорд и Нью-Йорк, 1971);
• Х. Кляйнерт , Калибровочные поля в конденсированном состоянии , Vol. I, «СУПЕРПОТОК И ВИХРЕВЫЕ ЛИНИИ», стр. 1–742, Том. II, «НАПРЯЖЕНИЯ И ДЕФЕКТЫ», стр. 743–1456, World Scientific (Сингапур, 1989) ; Мягкая обложка ISBN   9971-5-0210-0 (также доступен онлайн: Том I и Том II )

Внешние ссылки

• XY-модель в реальном времени, симуляция WebGL
• Интерактивное моделирование Монте-Карло моделей Изинга, XY и Гейзенберга с 3D-графикой (требуется браузер, совместимый с WebGL)