Конвекция Рэлея – Бенара

Продолжительность: 27 секунд. 0:27

Клетки Бенара.

В термодинамике жидкости конвекция Рэлея-Бенара представляет собой тип естественной конвекции , происходящей в плоском горизонтальном слое жидкости , нагретой снизу, в котором жидкость образует регулярный образец конвекционных ячеек, известных как ячейки Бенара . Такие системы впервые исследовал Жозеф Валентин Буссинеск. и Антон Обербек в 19 ​​веке. Это явление также может проявляться, когда вещество, более плотное, чем электролит, потребляется снизу и образуется вверху. Конвекция Бенара – Рэлея является одним из наиболее часто изучаемых явлений конвекции из-за ее аналитической и экспериментальной доступности. Модели конвекции являются наиболее тщательно изученным примером самоорганизующихся нелинейных систем . Известны зависящие от времени автомодельные аналитические решения для полей скорости, а также для распределения температуры.

Плавучесть , а значит и гравитация , ответственны за появление конвекционных ячеек. Первоначальное движение представляет собой подъем менее плотной жидкости из более теплого придонного слоя. Этот апвеллинг спонтанно организуется в регулярную структуру клеток.

Конвекция Рэлея-Бенара создает сложную картину повреждения травы морозом. Области с морозом через несколько дней становятся коричневыми, а области без мороза остаются зелеными. Пространственный масштаб рисунка ~20см.

Физические процессы

Особенности конвекции Бенара можно получить с помощью простого эксперимента, впервые проведенного французским физиком Анри Бенаром в 1900 году.

Развитие конвекции

Конвекционные ячейки в гравитационном поле

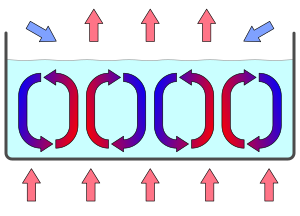
В экспериментальной установке используется слой жидкости, например воды, между двумя параллельными плоскостями. Высота слоя мала по сравнению с горизонтальным размером. Сначала температура нижней плоскости такая же, как и у верхней. Тогда жидкость будет стремиться к равновесию , при котором ее температура будет такой же, как и температура окружающей среды. (Оказавшись там, жидкость становится совершенно однородной: наблюдателю она будет казаться одинаковой из любого положения. Это равновесие также асимптотически устойчиво : после локального временного возмущения внешней температуры она вернется в свое однородное состояние, в соответствует второму началу термодинамики ).

Затем температура нижней плоскости немного увеличивается, создавая поток тепловой энергии, проходящий через жидкость. Система начнет иметь структуру теплопроводности : температура, а вместе с ней плотность и давление будут линейно меняться между нижней и верхней плоскостями. Будет установлен равномерный линейный градиент температуры. (Эта система может быть смоделирована статистической механикой ).

Как только проводимость устанавливается, микроскопическое случайное движение самопроизвольно становится упорядоченным на макроскопическом уровне, образуя конвекционные ячейки Бенара с характерной корреляционной длиной.

Особенности конвекции

Моделирование конвекции Рэлея – Бенара в 3D.

Вращение ячеек стабильно и будет чередоваться по часовой стрелке и против часовой стрелки по горизонтали; это пример спонтанного нарушения симметрии . Клетки Бенара метастабильны . Это значит, что небольшое возмущение не сможет изменить вращение ячеек, а большее может повлиять на вращение; они демонстрируют форму гистерезиса .

Более того, детерминированный закон на микроскопическом уровне приводит к недетерминированному расположению ячеек: если эксперимент повторяется, определенная позиция в эксперименте будет находиться в ячейке по часовой стрелке в одних случаях и в ячейке против часовой стрелки в других. Микроскопических возмущений начальных условий достаточно, чтобы вызвать недетерминированный макроскопический эффект. То есть в принципе невозможно рассчитать макроскопический эффект микроскопического возмущения. Эта неспособность предсказать условия на большие расстояния и чувствительность к начальным условиям являются характеристиками хаотичных или сложных систем (т.е. эффект бабочки ).

Продолжительность: 17 секунд. 0:17

турбулентная конвекция Рэлея – Бенара

Если бы температуру нижней плоскости еще больше повысить, структура стала бы более сложной в пространстве и времени; турбулентный поток станет хаотичным .

Конвективные ячейки Бенара имеют тенденцию приближаться к правильным шестиугольным призмам, особенно в отсутствие турбулентности. хотя определенные экспериментальные условия могут привести к образованию правильных прямоугольных призм. или спирали.

Конвективные ячейки Бенара не уникальны и обычно появляются только в результате конвекции, вызванной поверхностным натяжением. В общем случае решения Рэлея и Пирсона анализ (линейная теория), предполагающий бесконечный горизонтальный слой, приводит к вырождению, что означает, что система может получить множество шаблонов. Если предположить, что температура на верхней и нижней пластинах одинакова, то при использовании реалистичной системы (слоя с горизонтальными границами) форма границ будет определять шаблон. Чаще всего конвекция проявляется в виде валков или их суперпозиции.

Неустойчивость Рэлея – Бенара.

Поскольку между верхней и нижней пластинами существует градиент плотности, сила тяжести пытается притянуть более холодную и плотную жидкость сверху вниз. Этой гравитационной силе противостоит сила вязкого демпфирования в жидкости. Баланс этих двух сил выражается безразмерным параметром, называемым числом Рэлея . Число Рэлея определяется как:

$\mathrm {Ra} _{L}={\frac {g\beta }{\nu \alpha }}(T_{b}-T_{u})L^{3}$

где

T _u – температура верхней пластины

T _b – температура нижней пластины

L — высота контейнера

g - ускорение свободного падения

ν — кинематическая вязкость

α – коэффициент температуропроводности

β – коэффициент теплового расширения .

По мере увеличения числа Рэлея гравитационные силы становятся более доминирующими. При критическом числе Рэлея 1708 наступает нестабильность и появляются конвекционные ячейки.

Критическое число Рэлея можно получить аналитически для ряда различных граничных условий, выполнив анализ возмущений линеаризованных уравнений в устойчивом состоянии. Простейшим случаем является случай двух свободных границ, который лорд Рэлей решил в 1916 году, получив Ra = 27 ⁄ 4 п. ⁴  ≈ 657.51. В случае жесткой границы внизу и свободной границы вверху (как в случае чайника без крышки) критическое число Рэлея получается Ra = 1100,65.

Эффекты поверхностного натяжения

Основная статья: Эффект Марангони

В случае свободной поверхности жидкости, контактирующей с воздухом, эффекты плавучести и поверхностного натяжения также будут играть роль в развитии закономерностей конвекции. Жидкости текут из мест с меньшим поверхностным натяжением в места с более высоким поверхностным натяжением. Это называется эффектом Марангони . При подаче тепла снизу температура верхнего слоя будет колебаться. С повышением температуры поверхностное натяжение уменьшается. При этом будет иметь место боковое течение жидкости у поверхности, из более теплых мест в более прохладные. Чтобы сохранить горизонтальную (или почти горизонтальную) поверхность жидкости, более холодная поверхностная жидкость будет опускаться. Этот спуск более холодной жидкости способствует движущей силе конвекционных ячеек. Конкретный случай изменений поверхностного натяжения, вызванных градиентом температуры, известен как термокапиллярная конвекция или конвекция Бенара – Марангони.

История и номенклатура

В 1870 году ирландско-шотландский физик и инженер Джеймс Томсон (1822–1892), старший брат лорда Кельвина , наблюдал охлаждение воды в ванне; он отметил, что мыльная пленка на поверхности воды была разделена, как если бы поверхность была выложена плиткой (мозаичной). В 1882 году он показал, что мозаика возникла из-за присутствия конвекционных ячеек. французский физик Анри Бенар . В 1900 году к такому же выводу независимо пришел Эта модель конвекции, эффекты которой обусловлены исключительно температурным градиентом, была впервые успешно проанализирована в 1916 году лордом Рэлеем . Рэлей предположил граничные условия, при которых вертикальная составляющая скорости и температурное возмущение исчезают на верхней и нижней границах (идеальная теплопроводность). Эти предположения привели к тому, что анализ потерял всякую связь с экспериментом Анри Бенара. Это приводило к расхождениям между теоретическими и экспериментальными результатами до 1958 года, когда Джон Пирсон (1930–) переработал проблему, основанную на поверхностном натяжении. Именно это первоначально наблюдал Бенар. Тем не менее, в современном использовании «конвекция Рэлея – Бенара» относится к эффектам, обусловленным температурой, тогда как «конвекция Бенара – Марангони» относится конкретно к эффектам поверхностного натяжения. Дэвис и Кошмидер предположили, что конвекцию следует по праву называть «конвекцией Пирсона – Бенара».

Конвекцию Рэлея – Бенара также иногда называют «конвекцией Бенара – Рэлея», «конвекцией Бенара» или «конвекцией Рэлея».

См. также

• Гидродинамическая устойчивость
• Эффект Марангони
• Естественная конвекция
• Дорога гигантов и побережье Козуэй
• Нестабильность Рэлея – Тейлора

Дальнейшее чтение

• Б. Зальцман (ред., 1962). Избранные статьи по теории тепловой конвекции с особым применением к планетарной атмосфере Земли (Дувр).
• Субраманьян Чандрасекхар (1982). Гидродинамическая и гидромагнитная устойчивость (Дувр). ISBN   0-486-64071-X
• Э. Л. Кошмидер (1993). Клетки Бенара и вихри Тейлора (издательство Кембриджского университета). ISBN   9780521402040
• А.В. Гетлинг (1998). Конвекция Рэлея-Бенара: структуры и динамика (World Scientific).
• Р. Мейер-Спаше (1999). Формирование узоров в вязких потоках: проблема Тейлора-Куэтта и конвекция Рэлея-Бенара (Биркхойзер, Базель).
• П.Г. Дразин и У.Х. Рид (2004). Гидродинамическая устойчивость, второе издание (Издательство Кембриджского университета).
• Р. Х. Зейтунян (2009). Конвекция в жидкостях: рациональный анализ и асимптотическое моделирование (Springer).
• ЭСК Чинг (2014). Статистика и масштабирование в турбулентной конвекции Рэлея-Бенара (Спрингер). ISBN   978-981-4560-22-1
• Д. Голюскин (2015). Конвекция с внутренним нагревом и конвекция Рэлея-Бенара (Спрингер). ISBN   9783319239392

Внешние ссылки

• А. Гетлинг, О. Брауш: Модели клеточного потока
• К. Дэниэлс, Б. Плапп, В. Пеш, О. Брауш, Э. Боденшац: Волнообразный хаос в конвекции наклонного слоя
• Карен Э. Дэниелс, Оливер Брауш, Вернер Пеш, Эберхард Боденшац: Конкуренция и бистабильность упорядоченных волнистости и хаос волн в конвекции наклонного слоя. Архивировано 2 января 2021 г. в Wayback Machine (PDF; 608 КБ).
• П. Субраманиан, О. Брауш, Э. Боденшац, К. Дэниелс, Т. Шнайдер В. Пеш: Пространственно-временные закономерности конвекции в наклонном слое (PDF; 5,3 МБ)