система Лоренца

Не путать с кривой Лоренца или распределением Лоренца .

Пример решения в аттракторе Лоренца, когда ρ = 28 , σ = 10 и β = 8 / 3

Система Лоренца — система обыкновенных дифференциальных уравнений, впервые изученная математиком и метеорологом Эдвардом Лоренцем . Он примечателен тем, что имеет хаотичные решения для определенных значений параметров и начальных условий. В частности, аттрактор Лоренца представляет собой набор хаотических решений системы Лоренца. Термин « эффект бабочки » в популярных средствах массовой информации может происходить из реального значения аттрактора Лоренца, а именно того, что несколько различных начальных хаотических состояний развиваются в фазовом пространстве таким образом, который никогда не повторяется, поэтому весь хаос непредсказуем. Это подчеркивает, что хаотические системы могут быть полностью детерминированными, но при этом оставаться непредсказуемыми по своей сути в течение длительных периодов времени. Поскольку хаос в системах постоянно нарастает, невозможно хорошо предсказать будущее систем. Например, даже небольшой взмах крыльев бабочки может направить мир на совершенно другую траекторию, например, вызвав ураган. Форма самого аттрактора Лоренца, изображенная на графике фазовое пространство также напоминает бабочку.

Обзор

Смотрите также: Теория хаоса § Новаторский вклад Лоренца в хаотическое моделирование

В 1963 году Эдвард Лоренц с помощью Эллен Феттер , отвечавшей за численное моделирование и цифры, и Маргарет Гамильтон , которая помогла в первоначальных численных расчетах, приведших к выводам модели Лоренца, разработал упрощенную математическую модель атмосферной конвекции . Модель представляет собой систему трех обыкновенных дифференциальных уравнений, известных теперь как уравнения Лоренца:

${\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma (y-x),\\[6pt]{\frac {\mathrm {d} y}{\mathrm {d} t}}&=x(\rho -z)-y,\\[6pt]{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-\beta z.\end{aligned}}$

Уравнения связывают свойства двумерного слоя жидкости, равномерно нагретого снизу и охлаждаемого сверху. В частности, уравнения описывают скорость изменения трех величин во времени: x пропорционален скорости конвекции, y - горизонтальному изменению температуры и z - вертикальному изменению температуры. Константы σ , ρ и β являются параметрами системы, пропорциональными числу Прандтля , числу Рэлея и некоторым физическим размерам самого слоя.

Уравнения Лоренца могут возникать в упрощенных моделях лазеров . динамо-машины , термосифоны , бесщеточные двигатели постоянного тока , электрические цепи , химические реакции и прямой осмос . Уравнения Лоренца также являются основными уравнениями в пространстве Фурье для водяного колеса Малкуса . Водяное колесо Малкуса демонстрирует хаотическое движение, при котором вместо вращения в одном направлении с постоянной скоростью его вращение ускоряется, замедляется, останавливается, меняет направление и непредсказуемо колеблется вперед и назад между комбинациями такого поведения.

С технической точки зрения система Лоренца является нелинейной , апериодической, трехмерной и детерминированной . Уравнения Лоренца были предметом сотен научных статей и, по крайней мере, одного исследования объемом в книгу.

Анализ

Обычно предполагается, что параметры σ , ρ и β положительны. Лоренц использовал значения σ = 10 , β = 8/3 ​ = и ρ 28 . Система демонстрирует хаотическое поведение для этих (и близлежащих) значений.

Если ρ < 1 , то существует только одна точка равновесия, которая находится в начале координат. Эта точка соответствует отсутствию конвекции. Все орбиты сходятся к началу координат, которое является глобальным аттрактором , когда ρ < 1 .

происходит Бифуркация вил при ρ = 1 , а при ρ > 1 появляются две дополнительные критические точки при $$\left({\sqrt {\beta (\rho -1)}},{\sqrt {\beta (\rho -1)}},\rho -1\right)\quad {\text{and}}\quad \left(-{\sqrt {\beta (\rho -1)}},-{\sqrt {\beta (\rho -1)}},\rho -1\right).$$ Они соответствуют устойчивой конвекции. Эта пара точек равновесия устойчива только в том случае, если

$\rho <\sigma {\frac {\sigma +\beta +3}{\sigma -\beta -1}},$

которое может иметь место только для положительного ρ, если σ > β + 1 . При критическом значении обе точки равновесия теряют устойчивость из-за докритической бифуркации Хопфа .

Когда ρ = 28 , σ = 10 и β = 8/3 ( но , система Лоренца имеет хаотические решения не все решения хаотичны). Почти все начальные точки будут стремиться к инвариантному множеству – аттрактору Лоренца – странному аттрактору , фракталу и самовозбуждающемуся аттрактору относительно всех трёх равновесий. Его хаусдорфова размерность оценивается сверху по размерности Ляпунова (размерность Каплана-Йорка) как 2,06 ± 0,01 , а размерность корреляции оценивается в 2,05 ± 0,01 . Точную формулу размерности Ляпунова глобального аттрактора можно найти аналитически при классических ограничениях на параметры:

$3-{\frac {2(\sigma +\beta +1)}{\sigma +1+{\sqrt {\left(\sigma -1\right)^{2}+4\sigma \rho }}}}$

Аттрактор Лоренца сложно анализировать, но действие дифференциального уравнения на аттрактор описывается достаточно простой геометрической моделью. Доказательство того, что это действительно так, является четырнадцатой задачей в списке проблем Смейла . Эта проблема была первой, которую решил Уорвик Такер в 2002 году.

При других значениях ρ система отображает завязанные периодические орбиты. Например, при ρ = 99,96 он становится T (3,2) торическим узлом .

Примеры решений системы Лоренца для разных значений ρ
ρ = 14, σ = 10, β = 8 / 3 (Увеличивать)	ρ = 13, σ = 10, β = 8 / 3 (Увеличивать)
ρ = 15, σ = 10, β = 8 / 3 (Увеличивать)	ρ = 28, σ = 10, β = 8 / 3 (Увеличивать)
При малых значениях ρ система устойчива и развивается к одному из двух аттракторов с неподвижной точкой. При ρ > 24,74 неподвижные точки становятся отталкивателями и траектория отталкивается ими весьма сложным образом.

Чувствительная зависимость от начального состояния
Время t = 1 (Увеличивать)	Время t = 2 (Увеличивать)	Время t = 3 (Увеличивать)
Эти цифры получены с использованием ρ = 28 , σ = 10 и β = 8/3 10 . — показаны три временных отрезка трехмерной эволюции двух траекторий (одна синего цвета, другая желтого цвета) в аттракторе Лоренца, начинающихся в двух начальных точках, отличающихся всего на −5 в координате х . Первоначально две траектории кажутся совпадающими (видна только желтая, поскольку она нарисована поверх синей), но через некоторое время расхождение становится очевидным.

Подключение к карте палаток

Воссоздание результатов Лоренца, созданное в системе Mathematica . Точки над красной линией соответствуют лепесткам переключения системы.

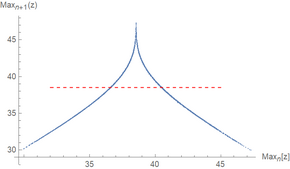
На рисунке 4 его статьи Лоренц построил график относительного максимального значения в направлении z, достигнутого системой, против предыдущего относительного максимума в направлении z . Эта процедура позже стала известна как карта Лоренца (не путать с графиком Пуанкаре , который отображает пересечения траектории с заданной поверхностью). Полученный график имеет форму, очень похожую на карту палатки . Лоренц также обнаружил, что когда максимальное значение z превышает определенный порог, система переключается на следующий лепесток. Объединив это с хаосом, который, как известно, демонстрирует карта палатки, он показал, что система хаотично переключается между двумя лепестками.

система

За последние несколько лет серия статей, посвященных многомерным моделям Лоренца, привела к появлению обобщенной модели Лоренца: которую можно упростить до классической модели Лоренца для трех переменных состояния или до следующей пятимерной модели Лоренца для пяти переменных состояния: $${\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma (y-x),\\[6pt]{\frac {\mathrm {d} y}{\mathrm {d} t}}&=x(\rho -z)-y,\\[6pt]{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-xy_{1}-\beta z,\\[6pt]{\frac {\mathrm {d} y_{1}}{\mathrm {d} t}}&=xz-2xz_{1}-d_{0}y_{1},\\[6pt]{\frac {\mathrm {d} z_{1}}{\mathrm {d} t}}&=2xy_{1}-4\beta z_{1}.\end{aligned}}$$

Выбор параметра ${\textstyle d_{0}={\dfrac {19}{3}}}$ был применен для согласования с выбором других параметров. Подробности смотрите в.

Моделирование

Джулия Моделирование

Моделирование Джулии

using Plots
# define the Lorenz attractor
@kwdef mutable struct Lorenz
    dt::Float64 = 0.02
    σ::Float64 = 10
    ρ::Float64 = 28
    β::Float64 = 8/3
    x::Float64 = 2
    y::Float64 = 1
    z::Float64 = 1
end

function step!(l::Lorenz)
    dx = l.σ * (l.y - l.x);         l.x += l.dt * dx
    dy = l.x * (l.ρ - l.z) - l.y;   l.y += l.dt * dy
    dz = l.x * l.y - l.β * l.z;     l.z += l.dt * dz
end

attractor = Lorenz()

# initialize a 3D plot with 1 empty series
plt = plot3d(
    1,
    xlim = (-30, 30),
    ylim = (-30, 30),
    zlim = (0, 60),
    title = "Lorenz Attractor",
    marker = 2,
)

# build an animated gif by pushing new points to the plot, saving every 10th frame
@gif for i=1:1500
    step!(attractor)
    push!(plt, attractor.x, attractor.y, attractor.z)
end every 10

Имитация клена

deq := [diff(x(t), t) = 10*(y(t) - x(t)), diff(y(t), t) = 28*x(t) - y(t) - x(t)*z(t), diff(z(t), t) = x(t)*y(t) - 8/3*z(t)]:
with(DEtools):
DEplot3d(deq, {x(t), y(t), z(t)}, t = 0 .. 100, [[x(0) = 10, y(0) = 10, z(0) = 10]], stepsize = 0.01, x = -20 .. 20, y = -25 .. 25, z = 0 .. 50, linecolour = sin(t*Pi/3), thickness = 1, orientation = [-40, 80], title = `Lorenz Chaotic Attractor`);

Максимальное моделирование

[sigma, rho, beta]: [10, 28, 8/3]$
eq: [sigma*(y-x), x*(rho-z)-y, x*y-beta*z]$
sol: rk(eq, [x, y, z], [1, 0, 0], [t, 0, 50, 1/100])$
len: length(sol)$
x: makelist(sol[k][2], k, len)$
y: makelist(sol[k][3], k, len)$
z: makelist(sol[k][4], k, len)$
draw3d(points_joined=true, point_type=-1, points(x, y, z), proportional_axes=xyz)$

Моделирование MATLAB

% Solve over time interval [0,100] with initial conditions [1,1,1]
% ''f'' is set of differential equations
% ''a'' is array containing x, y, and z variables
% ''t'' is time variable

sigma = 10;
beta = 8/3;
rho = 28;
f = @(t,a) [-sigma*a(1) + sigma*a(2); rho*a(1) - a(2) - a(1)*a(3); -beta*a(3) + a(1)*a(2)];
[t,a] = ode45(f,[0 100],[1 1 1]);     % Runge-Kutta 4th/5th order ODE solver
plot3(a(:,1),a(:,2),a(:,3))

Моделирование Mathematica

Стандартный способ:

tend = 50;
eq = {x'[t] == σ (y[t] - x[t]), 
      y'[t] == x[t] (ρ - z[t]) - y[t], 
      z'[t] == x[t] y[t] - β z[t]};
init = {x[0] == 10, y[0] == 10, z[0] == 10};
pars = {σ->10, ρ->28, β->8/3};
{xs, ys, zs} = 
  NDSolveValue[{eq /. pars, init}, {x, y, z}, {t, 0, tend}];
ParametricPlot3D[{xs[t], ys[t], zs[t]}, {t, 0, tend}]

Менее многословно:

lorenz = NonlinearStateSpaceModel[{{σ (y - x), x (ρ - z) - y, x y - β z}, {}}, {x, y, z}, {σ, ρ, β}];
soln[t_] = StateResponse[{lorenz, {10, 10, 10}}, {10, 28, 8/3}, {t, 0, 50}];
ParametricPlot3D[soln[t], {t, 0, 50}]

Симуляция Python

import matplotlib.pyplot as plt
import numpy as np

def lorenz(xyz, *, s=10, r=28, b=2.667):
    """
    Parameters
    ----------
    xyz : array-like, shape (3,)
       Point of interest in three-dimensional space.
    s, r, b : float
       Parameters defining the Lorenz attractor.

    Returns
    -------
    xyz_dot : array, shape (3,)
       Values of the Lorenz attractor's partial derivatives at *xyz*.
    """
    x, y, z = xyz
    x_dot = s*(y - x)
    y_dot = r*x - y - x*z
    z_dot = x*y - b*z
    return np.array([x_dot, y_dot, z_dot])

dt = 0.01
num_steps = 10000

xyzs = np.empty((num_steps + 1, 3))  # Need one more for the initial values
xyzs[0] = (0., 1., 1.05)  # Set initial values
# Step through "time", calculating the partial derivatives at the current point
# and using them to estimate the next point
for i in range(num_steps):
    xyzs[i + 1] = xyzs[i] + lorenz(xyzs[i]) * dt

# Plot
ax = plt.figure().add_subplot(projection='3d')

ax.plot(*xyzs.T, lw=0.6)
ax.set_xlabel("X Axis")
ax.set_ylabel("Y Axis")
ax.set_zlabel("Z Axis")
ax.set_title("Lorenz Attractor")

plt.show()

R-симуляция

R-моделирование

library(deSolve)
library(plotly)
# parameters
prm <- list(sigma = 10, rho = 28, beta = 8/3)
# initial values
varini <- c(
  X = 1,
  Y = 1, 
  Z = 1
)

Lorenz <- function (t, vars, prm) {
  with(as.list(vars), {
    dX <- prm$sigma*(Y - X)
    dY <- X*(prm$rho - Z) - Y
    dZ <- X*Y - prm$beta*Z
    return(list(c(dX, dY, dZ)))
   })
}

times <- seq(from = 0, to = 100, by = 0.01)
# call ode solver
out <- ode(y = varini, times = times, func = Lorenz,
           parms = prm)

# to assign color to points
gfill <- function (repArr, long) {
  rep(repArr, ceiling(long/length(repArr)))[1:long]
}

dout <- as.data.frame(out)

dout$color <- gfill(rainbow(10), nrow(dout))

# Graphics production with Plotly:
plot_ly(
  data=dout, x = ~X, y = ~Y, z = ~Z,
  type = 'scatter3d', mode = 'lines',
  opacity = 1, line = list(width = 6, color = ~color, reverscale = FALSE)
)

Приложения

атмосферной

Как показано в оригинальной статье Лоренца, Система Лоренца представляет собой уменьшенную версию более крупной системы, изученной ранее Барри Зальцманом. Уравнения Лоренца выводятся из приближения Обербека–Буссинеска к уравнениям, описывающим циркуляцию жидкости в неглубоком слое жидкости, равномерно нагретой снизу и равномерно охлаждаемой сверху. Эта циркуляция жидкости известна как конвекция Рэлея-Бенара . Предполагается, что жидкость циркулирует в двух измерениях (вертикальном и горизонтальном) с периодическими прямоугольными граничными условиями.

и температуру системы, Уравнения в частных производных, моделирующие функцию тока подвергаются спектральному приближению Галёркина : гидродинамические поля разлагаются в ряды Фурье, которые затем сильно усекаются до одного члена для функции тока и двух членов для температуры. Это сводит уравнения модели к набору из трех связанных нелинейных обыкновенных дифференциальных уравнений. Подробный вывод можно найти, например, в текстах по нелинейной динамике из Hilborn (2000) , Приложение C; Берже, Помо и Видаль (1984) , Приложение D; или Шен (2016), Дополнительные материалы.

природы хаоса и порядка

Научное сообщество признает, что хаотические особенности, обнаруженные в низкоразмерных моделях Лоренца, могут отражать особенности земной атмосферы ( ), что приводит к утверждению «погода хаотична». Для сравнения, на основе концепции сосуществования аттракторов в рамках обобщенной модели Лоренца. и исходная модель Лоренца ( ), Шен и его соавторы предложил пересмотренную точку зрения, согласно которой «погода сочетает в себе как хаос, так и порядок с четкой предсказуемостью». Пересмотренная точка зрения, которая является развитием традиционной точки зрения, используется, чтобы предположить, что «хаотичные и регулярные особенности, обнаруженные в теоретических моделях Лоренца, могут лучше отражать особенности атмосферы Земли».

Смейла

14-я задача Смейла гласит: «Являются ли свойства аттрактора Лоренца свойствами странного аттрактора ?». На эту проблему утвердительно ответил Уорвик Такер в 2002 году. Чтобы доказать этот результат, Такер использовал строгие числовые методы, такие как интервальная арифметика и нормальные формы . Во-первых, Такер определил поперечное сечение $\Sigma \subset \{x_{3}=r-1\}$ которая пересекается поперек траекториями потока. Отсюда можно определить карту первого возврата $P$, который присваивает каждому $x\in \Sigma$ суть $P(x)$ где траектория $x$ сначала пересекается $\Sigma$.

Затем доказательство разбивается на три основных пункта, которые доказаны и предполагают существование странного аттрактора. Три пункта:

• Есть такой регион $N\subset \Sigma$ инвариант относительно карты первого возврата, что означает $P(N)\subset N$.
• Карта возврата допускает поле конуса, инвариантное вперед.
• Векторы внутри этого инвариантного конусного поля равномерно разлагаются по производной $DP$ карты возврата.

Для доказательства первого пункта заметим, что сечение $\Sigma$ разрезается двумя дугами, образованными $P(\Sigma )$. Такер закрывает расположение этих двух дуг маленькими прямоугольниками. $R_{i}$, объединение этих прямоугольников дает $N$. Теперь цель состоит в том, чтобы доказать, что для всех точек в $N$, поток вернет точки в $\Sigma$, в $N$. Для этого мы составляем план $\Sigma '$ ниже $\Sigma$ на расстоянии $h$ маленький, то взяв центр $c_{i}$ из $R_{i}$ и используя метод интегрирования Эйлера, можно оценить, куда приведет поток $c_{i}$ в $\Sigma '$ что дает нам новую точку $c_{i}'$. Затем можно оценить, где находятся точки в $\Sigma$ будет отображено в $\Sigma '$ используя расширение Тейлора, мы получаем новый прямоугольник $R_{i}'$ сосредоточено на $c_{i}$. Таким образом, мы знаем, что все точки в $R_{i}$ будет отображено в $R_{i}'$. Цель состоит в том, чтобы выполнить этот метод рекурсивно, пока поток не вернется к $\Sigma$ и мы получаем прямоугольник $Rf_{i}$ в $\Sigma$ так, что мы это знаем $P(R_{i})\subset Rf_{i}$. Проблема в том, что наша оценка может стать неточной после нескольких итераций, поэтому Такер разбивает $R_{i}'$ на меньшие прямоугольники $R_{i,j}$ а затем применить процесс рекурсивно. Другая проблема заключается в том, что по мере применения этого алгоритма поток становится более «горизонтальным». что приводит к резкому увеличению неточности. Чтобы этого не произошло, алгоритм меняет ориентацию сечений, становясь либо горизонтальной, либо вертикальной.

Галерея

• 
  Решение в аттракторе Лоренца, построенное с высоким разрешением в плоскости xz .
• 
  Решение в аттракторе Лоренца, представленное в виде SVG .
• Анимация, показывающая траектории нескольких решений в системе Лоренца.
• 
  Решение в аттракторе Лоренца, представленное в виде металлической проволоки, показывает направление и трехмерную структуру.
• Анимация, показывающая расхождение ближайших решений системы Лоренца.
• 
  Визуализация аттрактора Лоренца вблизи прерывистого цикла.
• 
  Две линии тока в системе Лоренца от ρ = 0 до ρ = 28 ( σ = 10 , β = 8 / 3 ).
• 
  Анимация системы Лоренца с ро-зависимостью.
• 
  Анимация аттрактора Лоренца в Brain Dynamics Toolbox.

См. также

• Гипотеза Идена о размерности Ляпунова
• Модель Лоренц 96
• Список хаотичных карт
• Теорема Такенса

Ссылки

• Берже, Пьер; Помо, Ив; Видаль, Кристиан (1984). Порядок внутри хаоса: к детерминистическому подходу к турбулентности . Нью-Йорк: Джон Уайли и сыновья . ISBN  978-0-471-84967-4 .
• Куомо, Кевин М.; Оппенгейм, Алан В. (1993). «Схема реализации синхронизированного хаоса с приложениями к коммуникациям». Письма о физических отзывах . 71 (1): 65–68. Бибкод : 1993PhRvL..71...65C . дои : 10.1103/PhysRevLett.71.65 . ISSN   0031-9007 . ПМИД   10054374 .
• Горман, М.; Видманн, П.Дж.; Роббинс, Калифорния (1986). «Нелинейная динамика конвекционной петли: количественное сравнение эксперимента с теорией». Физика Д. 19 (2): 255–267. Бибкод : 1986PhyD...19..255G . дои : 10.1016/0167-2789(86)90022-9 .
• Грассбергер, П.; Прокачча, И. (1983). «Измерение странности странных аттракторов». Физика Д. 9 (1–2): 189–208. Бибкод : 1983PhyD....9..189G . дои : 10.1016/0167-2789(83)90298-1 .
• Хакен, Х. (1975). «Аналогия между высшими нестабильностями в жидкостях и лазерах». Буквы по физике А. 53 (1): 77–78. Бибкод : 1975PhLA...53...77H . дои : 10.1016/0375-9601(75)90353-9 .
• Хемати, Н. (1994). «Странные аттракторы в бесщеточных двигателях постоянного тока». Транзакции IEEE в схемах и системах I: Фундаментальная теория и приложения . 41 (1): 40–45. дои : 10.1109/81.260218 . ISSN   1057-7122 .
• Хилборн, Роберт С. (2000). Хаос и нелинейная динамика: введение для ученых и инженеров (второе изд.). Издательство Оксфордского университета . ISBN  978-0-19-850723-9 .
• Хирш, Моррис В .; Смейл, Стивен ; Девани, Роберт (2003). Дифференциальные уравнения, динамические системы и введение в хаос (второе изд.). Бостон, Массачусетс: Академическая пресса . ISBN  978-0-12-349703-1 .
• Кноблох, Эдгар (1981). «Хаос в динамо-машине с сегментированным диском». Буквы по физике А. 82 (9): 439–440. Бибкод : 1981PhLA...82..439K . дои : 10.1016/0375-9601(81)90274-7 .
• Коларж, Мирослав; Гамбс, Годфри (1992). «Теория экспериментального наблюдения хаоса во вращающемся водяном колесе». Физический обзор А. 45 (2): 626–637. Бибкод : 1992PhRvA..45..626K . дои : 10.1103/PhysRevA.45.626 . ПМИД   9907027 .
• Леонов Г.А.; Кузнецов Н.В.; Коржеманова Н.А.; Кусакин, Д.В. (2016). «Формула размерности Ляпунова для глобального аттрактора системы Лоренца» Коммуникации в нелинейной науке и численном моделировании . 41 : 84–103. arXiv : 1508.07498 . Бибкод : 2016CNSNS..41...84L . дои : 10.1016/j.cnsns.2016.04.032 . S2CID   119614076 .
• Лоренц, Эдвард Нортон (1963). «Детерминированный непериодический поток» . Журнал атмосферных наук . 20 (2): 130–141. Бибкод : 1963JAtS...20..130L . doi : 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 .
• Мишра, Аашвин; Санги, Санджив (2006). «Исследование асимметричного водяного колеса Малкуса: смещенные уравнения Лоренца». Хаос: междисциплинарный журнал нелинейной науки . 16 (1): 013114. Бибкод : 2006Хаос..16a3114M . дои : 10.1063/1.2154792 . ПМИД   16599745 .
• Пчелинцев, АН (2014). «Численное и физическое моделирование динамики системы Лоренца». Численный анализ и приложения . 7 (2): 159–167. дои : 10.1134/S1995423914020098 . S2CID   123023929 .
• Польша, Дуглас (1993). «Кооперативный катализ и химический хаос: химическая модель уравнений Лоренца». Физика Д. 65 (1): 86–99. Бибкод : 1993PhyD...65...86P . дои : 10.1016/0167-2789(93)90006-М .
• Зальцман, Барри (1962). «Свободная конвекция конечной амплитуды как задача начального значения — I» . Журнал атмосферных наук . 19 (4): 329–341. Бибкод : 1962JAtS...19..329S . doi : 10.1175/1520-0469(1962)019<0329:FAFCAA>2.0.CO;2 .
• Шен, Б.-В. (21 декабря 2015 г.). «Нелинейная обратная связь в шестимерной модели Лоренца: влияние дополнительного нагревательного члена». Нелинейные процессы в геофизике . 22 (6): 749–764. doi : 10.5194/npg-22-749-2015. ISSN 1607-7946.
• Воробей, Колин (1982). Уравнения Лоренца: бифуркации, хаос и странные аттракторы . Спрингер.
• Такер, Уорвик (2002). «Строгое решение ОДУ и 14-я проблема Смейла» (PDF) . Основы вычислительной математики . 2 (1): 53–117. CiteSeerX   10.1.1.545.3996 . дои : 10.1007/s002080010018 . S2CID   353254 .
• Ценов, Стефан (2014). «Странные аттракторы, характеризующие осмотическую нестабильность». arXiv : 1406.0979v1 [ physical.flu-dyn ].
• Виана, Марсело (2000). «Что нового о странных аттракторах Лоренца?». Математический интеллект . 22 (3): 6–19. дои : 10.1007/BF03025276 . S2CID   121427433 .
• Лоренц, Эдвард Н. (1960). «Статистическое предсказание решений динамических уравнений» (PDF) . Симпозиум по численному прогнозированию погоды в Токио . Архивировано из оригинала (PDF) 23 мая 2019 г. Проверено 16 сентября 2020 г.

Дальнейшее чтение

• Г. А. Леонов и Н. В. Кузнецов (2015). «О различиях и сходствах в анализе систем Лоренца, Чена и Лу» . Прикладная математика и вычислительная техника . 256 : 334–343. arXiv : 1409.8649 . дои : 10.1016/j.amc.2014.12.132 .
• Пчелинцев, АН (2022). «О высокоточном методе исследования аттракторов динамических систем и систем взрывного типа» . Математика . 10 (8): 1207. arXiv : 2206.08195 . дои : 10.3390/math10081207 .

Внешние ссылки

• «Аттрактор Лоренца» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Вайсштейн, Эрик В. «Аттрактор Лоренца» . Математический мир .
• Аттрактор Лоренца Роба Морриса, Демонстрационный проект Вольфрама .
• Уравнение Лоренца. Архивировано 7 июня 2009 г. в Wayback Machine на сайте Planetmath.org.
• Синхронизированный хаос и частные коммуникации, с Кевином Куомо . Реализация аттрактора Лоренца в электронной схеме.
• Интерактивная анимация аттрактора Лоренца (нужен плагин Adobe Shockwave)
• 3D Attractors: программа Mac для визуализации и исследования аттрактора Лоренца в трех измерениях.
• Аттрактор Лоренца реализован в аналоговой электронике
• Интерактивная анимация Lorenz Attractor (реализована на Ada с помощью GTK+. Исходные коды и исполняемый файл)
• Интерактивный веб-аттрактор Лоренца, созданный с использованием йодида.