Бифуркационная диаграмма

В математике , особенно в динамических системах , бифуркационная диаграмма показывает значения, которые посещаются или приближаются асимптотически (неподвижные точки, периодические орбиты или хаотические аттракторы ) системы как функция параметра бифуркации в системе. Обычно стабильные значения обозначаются сплошной линией, а нестабильные значения — пунктирной линией, хотя часто нестабильные точки опускаются. Бифуркационные диаграммы позволяют визуализировать теорию бифуркаций . В контексте динамических систем с дискретным временем диаграмма также называется орбитальной диаграммой .

Бифуркационная диаграмма логистической карты

Бифуркационная диаграмма круговой карты . Черные области соответствуют языкам Арнольда .

Логистическая карта

См. Также: Динамические системы и Список хаотических карт.

Бифуркационная диаграмма логистической карты . Аттрактор r для любого значения параметра r показан на вертикальной линии при этом .

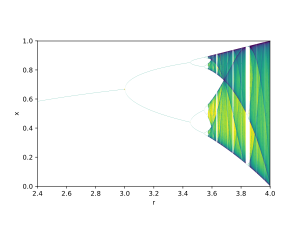
Примером может служить бифуркационная диаграмма логистической карты :

$$x_{n+1}=rx_{n}(1-x_{n}).$$

Параметр бифуркации r показан на горизонтальной оси графика, а вертикальная ось показывает набор значений логистической функции, посещаемой асимптотически почти из всех начальных условий.

Бифуркационная диаграмма показывает разветвление периодов устойчивых орбит от 1 до 2, от 4 до 8 и т. д. Каждая из этих точек бифуркации представляет собой бифуркацию удвоения периода .Отношение длин последовательных интервалов между значениями r , при которых происходит бифуркация, сходится к первой константе Фейгенбаума .

На диаграмме также показано удвоение периода от 3 до 6, до 12 и т. д., от 5 до 10, до 20 и т. д. и так далее.

Нарушение симметрии в бифуркационных множествах

Нарушение симметрии в бифуркации вил параметра ε при изменении . ε = 0 — случай симметричной вилочной бифуркации.

В такой динамической системе, как

$${\ddot {x}}+f(x;\mu )+\varepsilon g(x)=0,$$

который является структурно устойчивым, когда $\mu \neq 0$, если построить бифуркационную диаграмму, рассматривая $\mu$ как параметр бифуркации, но для разных значений $\varepsilon$, случай $\varepsilon =0$ представляет собой симметричную бифуркацию вил. Когда $\varepsilon \neq 0$, мы говорим, что у нас есть вилы с нарушенной симметрией. Это показано на анимации справа.

Приложения

Рассмотрим систему дифференциальных уравнений , описывающую некоторую физическую величину, которая для конкретности может представлять собой один из трех примеров: 1. положение и скорость незатухающего маятника без трения, 2. мембранный потенциал нейрона с течением времени и 3. среднюю концентрацию. вируса в кровотоке пациента. Дифференциальные уравнения для этих примеров включают *параметры*, которые могут повлиять на выходные данные уравнений. Изменение массы и длины маятника повлияет на частоту его колебаний, изменение величины тока, подаваемого в нейрон, может перевести мембранный потенциал из состояния покоя в пиковый, а долговременная вирусная нагрузка в кровотоке может снизиться при тщательно рассчитанном лечении.

В общем, исследователи могут попытаться количественно оценить, как меняется долгосрочное (асимптотическое) поведение системы дифференциальных уравнений при изменении параметра. В динамических систем разделе математики бифуркационная диаграмма количественно определяет эти изменения, показывая, как неподвижные точки, периодические орбиты или хаотические аттракторы системы изменяются в зависимости от параметра бифуркации . Для визуализации этих изменений используются бифуркационные диаграммы.

См. также

• Бифуркационная память
• Теория хаоса
• Скелет бифуркационной диаграммы
• Константы фигового дерева

Дальнейшее чтение

• Глендиннинг, Пол (1994). Стабильность, нестабильность и хаос . Издательство Кембриджского университета . ISBN  0-521-41553-5 .
• Мэй, Роберт М. (1976). «Простые математические модели с очень сложной динамикой». Природа . 261 (5560): 459–467. Бибкод : 1976Natur.261..459M . дои : 10.1038/261459a0 . hdl : 10338.dmlcz/104555 . ПМИД   934280 . S2CID   2243371 .
• Строгац, Стивен (2000). Нелинейная динамика и хаос: с приложениями к физике, биологии, химии и технике . Книги Персея . ISBN  0-7382-0453-6 .

Внешние ссылки

• Логистическая карта и хаос , Элмер Г. Винс, egwald.ca
• Викиверситет: Диаграмма орбиты динамической системы дискретного времени