Бифуркация удвоения периода

В теории динамических систем происходит бифуркация удвоения периода , когда небольшое изменение параметров системы приводит к появлению новой периодической траектории из существующей периодической траектории - новой, имеющей двойной период исходной. При удвоенном периоде вдвое дольше (или, в дискретной числовые значения, посещаемые системой, повторяются динамической системе, в два раза больше итераций).

Бифуркация сокращения периода вдвое происходит, когда система переключается на новое поведение с половиной периода исходной системы.

представляет Каскад удвоения периода собой бесконечную последовательность бифуркаций удвоения периода. Такие каскады являются распространенным путем, по которому динамические системы создают хаос. В гидродинамике они являются одним из возможных путей возникновения турбулентности .

Бифуркации сокращения периода вдвое (L), ведущие к порядку, за которыми следуют бифуркации удвоения периода (R), ведущие к хаосу.

Примеры

Бифуркационная диаграмма логистической карты. Он показывает значения аттрактора , например $x_{*}$ и $x'_{*}$, как функция параметра $r$.

Логистическая карта

– Логистическая карта это

$x_{n+1}=rx_{n}(1-x_{n})$

где $x_{n}$ является функцией (дискретного) времени $n=0,1,2,\ldots$. Параметр $r$ предполагается, что он лежит в интервале $[0,4]$, в этом случае $x_{n}$ ограничен $[0,1]$.

Для $r$ между 1 и 3, $x_{n}$ сходится к устойчивой неподвижной точке $x_{*}=(r-1)/r$. Тогда для $r$ от 3 до 3,44949, $x_{n}$ сходится к постоянному колебанию между двумя значениями $x_{*}$ и $x'_{*}$ это зависит от $r$. Как $r$ увеличивается, появляются колебания между 4 значениями, затем 8, 16, 32 и т. д. Эти удвоения периода достигают кульминации в $r\approx 3.56995$, за пределами которого появляются более сложные режимы. Как $r$ увеличивается, существуют некоторые интервалы, где большинство начальных значений сходятся к одному или небольшому количеству устойчивых колебаний, например, вблизи $r=3.83$.

В интервале, где период $2^{n}$ для некоторого положительного целого числа $n$, не все точки на самом деле имеют период $2^{n}$. Это отдельные точки, а не интервалы. Говорят, что эти точки находятся на нестабильных орбитах, поскольку близлежащие точки не приближаются к той же орбите, что и они.

Квадратичная карта

Реальная версия комплексного квадратичного отображения связана с реальным срезом множества Мандельброта .

• 
  Каскад удвоения периода в экспоненциальном отображении множества Мандельброта
• 
  1D-версия с экспоненциальным отображением
• 
  бифуркация удвоения периода

–

Удвоение периода в уравнении Курамото–Сивашинского с периодическими граничными условиями. Кривые изображают решения уравнения Курамото–Сивашинского, спроецированные на фазовую плоскость энергии (E, dE/dt) , где E – L ² -норма раствора. При ν = 0,056 существует периодическая орбита с периодом T ≈ 1,1759. Вблизи ν ≈ 0,0558 это решение распадается на 2 орбиты, которые далее расходятся по мере ν уменьшения . Точно при переходном значении ν новая орбита (обведена красным) имеет период в два раза больше исходной. (Однако при дальнейшем увеличении ν соотношение периодов отклоняется ровно от 2.)

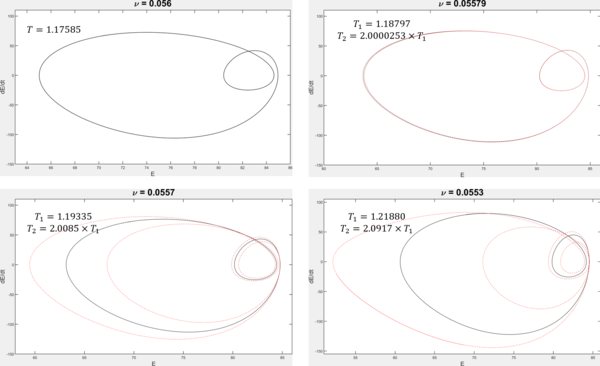
Уравнение Курамото -Сивашинского является примером непрерывной в пространстве и времени динамической системы, в которой наблюдается удвоение периода. Это одно из наиболее хорошо изученных нелинейных уравнений в частных производных , первоначально введенное как модель распространения фронта пламени.

Одномерное уравнение Курамото – Сивашинского имеет вид

$u_{t}+uu_{x}+u_{xx}+\nu \,u_{xxxx}=0$

Распространенным выбором граничных условий является пространственная периодичность: $u(x+2\pi ,t)=u(x,t)$.

Для больших значений $\nu$, $u(x,t)$ развивается в сторону стационарных (независящих от времени) решений или простых периодических орбит. Как $\nu$ снижается, динамика со временем развивается в хаос. Переход от порядка к хаосу происходит через каскад бифуркаций удвоения периода: один из которых показан на рисунке.

кривой

Рассмотрим следующую логистическую карту модифицированной кривой Филлипса :

$\pi _{t}=f(u_{t})+b\pi _{t}^{e}$

$\pi _{t+1}=\pi _{t}^{e}+c(\pi _{t}-\pi _{t}^{e})$

$f(u)=\beta _{1}+\beta _{2}e^{-u}\,$

$b>0,0\leq c\leq 1,{\frac {df}{du}}<0$

где :

• $\pi$ это фактическая инфляция
• $\pi ^{e}$ ожидаемая инфляция,
• u — уровень безработицы,
• $m-\pi$ – темп роста денежной массы .

Хранение $\beta _{1}=-2.5,\ \beta _{2}=20,\ c=0.75$ и различные $b$, система претерпевает бифуркации удвоения периода и в конечном итоге становится хаотичной.

Экспериментальное наблюдение

Удвоение периода наблюдалось в ряде экспериментальных систем. Существуют также экспериментальные доказательства каскадов удвоения периода. наблюдались последовательности четырех удвоений периода Например, в динамике конвекционных валов в воде и ртути . Аналогичным образом, 4-5 удвоений наблюдались в некоторых нелинейных электронных схемах . Однако точность эксперимента, необходимая для обнаружения i ^й событие удвоения в каскаде увеличивается экспоненциально с i , что затрудняет наблюдение более 5 событий удвоения в каскаде.

См. также

• Список хаотичных карт
• Комплексная квадратичная карта
• Константы фигового дерева
• Универсальность (динамические системы)
• Теорема Шарковского

Ссылки

• Аллигуд, Кэтлин Т.; Зауэр, Тим; Йорк, Джеймс (1996). Хаос: введение в динамические системы . Учебники по математическим наукам. Спрингер-Верлаг Нью-Йорк. дои : 10.1007/0-387-22492-0_3 . ISBN  978-0-387-94677-1 . ISSN   1431-9381 .
• Джильо, Марцио; Мусацци, Серджио; Перини, Умберто (1981). «Переход к хаотическому поведению через воспроизводимую последовательность бифуркаций удвоения периода». Письма о физических отзывах . 47 (4): 243–246. Бибкод : 1981PhRvL..47..243G . дои : 10.1103/PhysRevLett.47.243 . ISSN   0031-9007 .
• Калогиру, А.; Кивени, Э.Э.; Папагеоргиу, Д.Т. (2015). «Углубленное численное исследование двумерного уравнения Курамото – Сивашинского» . Труды Королевского общества A: Математические, физические и технические науки . 471 (2179): 20140932. Бибкод : 2015RSPSA.47140932K . дои : 10.1098/rspa.2014.0932 . ISSN   1364-5021 . ПМЦ   4528647 . ПМИД   26345218 .
• Кузнецов, Юрий А. (2004). Элементы прикладной теории бифуркаций . Прикладные математические науки. Том. 112 (3-е изд.). Спрингер-Верлаг . ISBN  0-387-21906-4 . Збл   1082.37002 .
• Либчабер, А.; Ларош, К.; Фов, С. (1982). «Каскад удвоения периода в ртути, количественное измерение» (PDF) . Журнал Physique Lettres . 43 (7): 211–216. doi : 10.1051/jphyslet:01982004307021100 . ISSN   0302-072X .
• Папагеоргиу, Д.Т.; Смирлис, Ю.С. (1991), "Путь к хаосу для уравнения Курамото-Сивашинского", Теорет. Вычислить. Гидродинамика , 3 (1): 15–42, Бибкод : 1991ThCFD...3...15P , doi : 10.1007/BF00271514 , hdl : 2060/19910004329 , ISSN   1432-2250 , S2CID   116955014
• Смирлис, Ю.С.; Папагеоргиу, Д.Т. (1991). «Прогнозирование хаоса для бесконечномерных динамических систем: уравнение Курамото-Сивашинского, практический пример» . Труды Национальной академии наук . 88 (24): 11129–11132. Бибкод : 1991PNAS...8811129S . дои : 10.1073/pnas.88.24.11129 . ISSN   0027-8424 . ПМК   53087 . ПМИД   11607246 .
• Строгац, Стивен (2015). Нелинейная динамика и хаос: с приложениями к физике, биологии, химии и технике (2-е изд.). ЦРК Пресс. ISBN  978-0813349107 .
• Чунг, ПЮ; Вонг, А.Ю. (1987). «Хаотическое поведение и удвоение периода в плазме». Письма о физических отзывах . 59 (5): 551–554. Бибкод : 1987PhRvL..59..551C . doi : 10.1103/PhysRevLett.59.551 . ISSN   0031-9007 . ПМИД   10035803 .

Внешние ссылки

• Связь каскадов удвоения периода с хаосом