Магнитное квантовое число

В атомной физике магнитное квантовое число — это квантовое число, используемое для различения квантовых состояний электрона или другой частицы в соответствии с его угловым моментом вдоль заданной оси в пространстве. Орбитальное магнитное квантовое число ( m _l или m ) различает орбитали, доступные внутри данной подоболочки атома. Он определяет компонент орбитального углового момента, который лежит вдоль данной оси, условно называемой осью z , поэтому он описывает ориентацию орбитали в пространстве. Спиновое магнитное квантовое число m _s определяет z по оси компонент спинового углового момента для частицы, имеющей спиновое квантовое число s . Для электрона s равно 1 ⁄ 2 , а m _s либо + 1 ⁄ 2 или - 1 ⁄ 2 , часто называемый «раскруткой вверх» и «раскруткой вниз», или α и β. Термин «магнитный» в названии относится к магнитному дипольному моменту, связанному с каждым типом углового момента, поэтому состояния, имеющие разные магнитные квантовые числа, смещаются по энергии в магнитном поле в соответствии с эффектом Зеемана .

Четыре квантовых числа, традиционно используемые для описания квантового состояния электрона в атоме, — это главное квантовое число n , азимутальное (орбитальное) квантовое число. $\ell$и магнитные квантовые числа m _l и m _s . Электроны в данной подоболочке атома (например, s, p, d или f) определяются значениями $\ell$ (0, 1, 2 или 3). Орбитальное магнитное квантовое число принимает целые значения в диапазоне от $-\ell$ к $+\ell$, включая ноль. Таким образом, подоболочки s, p, d и f содержат по 1, 3, 5 и 7 орбиталей каждая. На каждой из этих орбиталей может разместиться до двух электронов (с противоположными спинами), составляющих основу таблицы Менделеева .

Другие магнитные квантовые числа определяются аналогичным образом, например, m _j для z, компонента оси полного электронного углового момента j , и m _I для ядерного спина I . квантовые числа пишутся с заглавной буквы, чтобы указать общие суммы для системы частиц, например, ML _L или m _{Магнитные} для полного орбитального углового момента по оси z всех электронов в атоме.

Вывод

Эти орбитали имеют магнитные квантовые числа. $m_{l}=-\ell ,\ldots ,\ell$ слева направо в порядке возрастания. $e^{m_{l}i\phi }$ Зависимость азимутальной составляющей можно рассматривать как цветовой градиент, повторяющийся $m_{l}$ раз вокруг вертикальной оси.

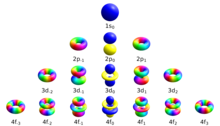
Существует набор квантовых чисел, связанных с энергетическими состояниями атома. Четыре квантовых числа $n$, $\ell$, $m_{l}$, и $m_{s}$ определить полное квантовое состояние одного электрона в атоме, называемое его волновой функцией или орбиталью . Уравнение Шрёдингера для волновой функции атома с одним электроном представляет собой разделяющееся уравнение в частных производных . (Это не относится к нейтральному атому гелия или другим атомам с взаимно взаимодействующими электронами, которые требуют более сложных методов решения. ) Это означает, что волновую функцию, выраженную в сферических координатах, можно разбить на произведение трех функций радиуса, угла широты (или полярности) и азимута:

$\psi (r,\theta ,\phi )=R(r)P(\theta )F(\phi )$

Дифференциальное уравнение для $F$ можно решить в виде $F(\phi )=Ae^{\lambda \phi }$. Поскольку значения азимутального угла $\phi$ отличаются на 2 $\pi$ радианы (360 градусов) представляют одно и то же положение в пространстве, а общая величина $F$ не растет со сколь угодно большими $\phi$ как и в случае с действительным показателем, коэффициент $\lambda$ должно быть квантовано до целого числа, кратного $i$, производя мнимую степень : $\lambda =im_{l}$. Эти целые числа являются магнитными квантовыми числами. Та же константа появляется в уравнении широты, где большие значения ${m_{l}}^{2}$ имеют тенденцию уменьшать величину $P(\theta ),$ и ценности $m_{l}$ больше азимутального квантового числа $\ell$ не допускайте какого-либо решения для $P(\theta ).$

Связь между квантовыми числами
орбитальный	Ценности	Количество значений для $m_{l}$	Электронов на подоболочку
с	$\ell =0,\quad m_{l}=0$	1	2
п	$\ell =1,\quad m_{l}=-1,0,+1$	3	6
д	$\ell =2,\quad m_{l}=-2,-1,0,+1,+2$	5	10
ж	$\ell =3,\quad m_{l}=-3,-2,-1,0,+1,+2,+3$	7	14
г	$\ell =4,\quad m_{l}=-4,-3,-2,-1,0,+1,+2,+3,+4$	9	18

Как составляющая углового момента

Иллюстрация квантовомеханического орбитального углового момента. Конусы и плоскость представляют собой возможные ориентации вектора углового момента для $\ell =2$ и $m_{l}=-2,-1,0,1,2$. Даже для крайних значений $m_{l}$, $z$-компонента этого вектора меньше его полной величины.

Ось, используемая для полярных координат в этом анализе, выбрана произвольно. Квантовое число $m_{l}$ относится к проекции углового момента в этом произвольно выбранном направлении, условно называемом $z$-направление или ось квантования . $L_{z}$, величина углового момента в $z$-направление, определяется формулой:

$L_{z}=m_{l}\hbar$.

Это составляющая полного орбитального углового момента атомного электрона. $\mathbf {L}$, величина которого связана с азимутальным квантовым числом его подоболочки $\ell$ по уравнению:

$L=\hbar {\sqrt {\ell (\ell +1)}}$,

где $\hbar$ – приведенная постоянная Планка . Обратите внимание, что это $L=0$ для $\ell =0$ и приближает $L=\left(\ell +{\tfrac {1}{2}}\right)\hbar$ для высокого $\ell$. Невозможно измерить угловой момент электрона по всем трем осям одновременно. Эти свойства были впервые продемонстрированы в эксперименте Штерна-Герлаха Отто Штерном и Вальтером Герлахом .

Эффект в магнитных полях

Квантовое число $m_{l}$ в общих чертах относится к направлению углового момента вектора . Магнитное квантовое число $m_{l}$ влияет на энергию электрона только в том случае, если он находится в магнитном поле, поскольку в отсутствие такового все сферические гармоники, соответствующие различным произвольным значениям $m_{l}$ эквивалентны. Магнитное квантовое число определяет энергетический сдвиг атомной орбитали из-за внешнего магнитного поля ( эффект Зеемана ) — отсюда и название магнитного квантового числа. Однако реальный магнитный дипольный момент электрона на атомной орбитали возникает не только из углового момента электрона, но и из спина электрона, выраженного в спиновом квантовом числе .

Поскольку каждый электрон обладает магнитным моментом в магнитном поле, на него будет действовать крутящий момент, который стремится сделать вектор $\mathbf {L}$ параллельно полю происходит явление, известное как ларморовская прецессия .

См. также

• Квантовое число
  • Азимутальное квантовое число
  • Главное квантовое число
  • Спиновое квантовое число
  • Квантовое число полного углового момента
• Электронная оболочка
• Основная квантовая механика
• атом Бора
• Уравнение Шрёдингера