Уравнение углового дома

В математической физике уравнение Экхауза – или уравнение Кунду – Экхауза – представляет собой нелинейное уравнение в частных производных в пределах нелинейного класса Шредингера :

$i\psi _{t}+\psi _{xx}+2\left(|\psi |^{2}\right)_{x}\,\psi +|\psi |^{4}\,\psi =0.$

Уравнение было независимо введено Виктором Экхаусом и Анджаном Кунду для моделирования распространения волн в средах с дисперсией .

Линеаризация

Анимация пакетного решения уравнения Экхауза. Синяя линия — действительная часть решения, красная линия — мнимая часть , а черная линия — огибающая волны ( абсолютное значение ). Обратите внимание на асимметрию конверта. $|\psi (x,t)|$ для уравнения Экхауза, а огибающая $|\varphi (x,t)|$ – соответствующего решения линейного уравнения Шрёдингера – симметрично (в $x$). Короткие волны в пакете распространяются быстрее, чем длинные волны.

Анимация пакетного решения линейного уравнения Шредингера , соответствующая приведенной выше анимации для уравнения Экхауза. Синяя линия — действительная часть решения, красная линия — мнимая часть , черная линия — огибающая волны ( абсолютное значение ), а зеленая линия — центр тяжести огибающей волнового пакета.

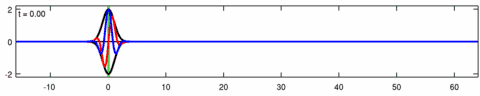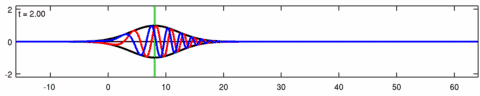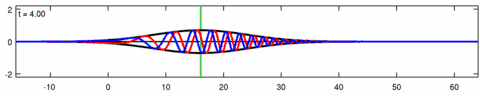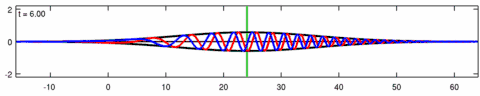
Уравнение Экхауза можно линеаризовать до линейного уравнения Шрёдингера :

$i\varphi _{t}+\varphi _{xx}=0,$

посредством нелинейного преобразования:

$\varphi (x,t)=\psi (x,t)\,\exp \left(\int _{-\infty }^{x}|\psi (x^{\prime },t)|^{2}\;{\text{d}}x^{\prime }\right).$

Обратное преобразование:

$\psi (x,t)={\frac {\varphi (x,t)}{\displaystyle \left(1+2\,\int _{-\infty }^{x}|\varphi (x^{\prime },t)|^{2}\;{\text{d}}x^{\prime }\right)^{1/2}}}.$

Из этой линеаризации также следует, что уравнение Экхауза интегрируемо .

Ссылки

• Абловиц, MJ ; Аренс, CD; Де Лилло, С. (2005), «О «квази» интегрируемом дискретном уравнении Экхауза», Журнал нелинейной математической физики , 12 (Приложение 1): 1–12, Бибкод : 2005JNMP...12S...1A , doi : 10.2991/jnmp.2005.12.s1.1 , S2CID   59441129
• Калоджеро, Ф .; Де Лилло, С. (1987), "УЧП Экхауса i ψ _t + ψ _xx + 2(|ψ| ² ) _x ψ + |ψ| ⁴ ψ = 0", Обратные задачи , 3 (4): 633–682, Бибкод : 1987InvPr...3..633C , doi : 10.1088/0266-5611/3/4/012 , S2CID   250876392
• Экхаус, В. (1985), Поведение возмущенных волновых уравнений и связанные с ними проблемы в длительном времени , факультет математики, Утрехтский университет, препринт №. 404 .
  Частично опубликовано в: Экхаус, В. (1986), «Поведение возмущенных волновых уравнений и связанных с ними проблем в длительном времени», Кренер, Э.; Кирхгесснер, К. (ред.), Тенденции в приложениях чистой математики к механике , Конспект лекций по физике, том. 249, Берлин: Springer, стр. 168–194, doi : 10.1007/BFb0016391 , ISBN.  978-3-540-16467-8
• Кунду, А. (1984), «Калибровка Ландау–Лифшица и нелинейных систем более высокого порядка, созданная на основе нелинейных уравнений типа Шредингера», Journal of Mathematical Physics , 25 (12): 3433–3438, Bibcode : 1984JMP....25.3433 К , дои : 10.1063/1.526113
• Тагизаде, Н.; Мирзазаде, М.; Таскан, Ф. (2012), «Метод первого интеграла, примененный к уравнению Экхауза», Applied Mathematics Letters , 25 (5): 798–802, doi : 10.1016/j.aml.2011.10.021
• Цвиллингер, Д. (1998), Справочник по дифференциальным уравнениям (3-е изд.), Academic Press, ISBN  978-0-12-784396-4