Квантовое число
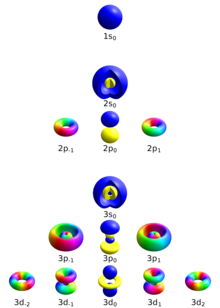
| Часть серии статей о |
| Квантовая механика |
|---|
В квантовой физике химии квантовые и числа — это величины, характеризующие возможные состояния системы. Квантовые числа тесно связаны с собственными значениями величин наблюдаемых . Когда соответствующая наблюдаемая коммутирует с гамильтонианом, квантовое число называется « хорошим » и действует как константа движения в квантовой динамике.
Чтобы полностью определить состояние электрона в атоме водорода, необходимы четыре квантовых числа. Традиционный набор квантовых чисел включает главное , азимутальное , магнитное и спиновое квантовые числа. Для описания других систем требуются другие квантовые числа. необходимо ввести новые квантовые числа, такие как аромат кварков Для субатомных частиц , которые не имеют классического соответствия.
История
[ редактировать ]Электронные квантовые числа
[ редактировать ]В эпоху старой квантовой теории , начиная с предложения Максом Планком квантов в его модели излучения черного тела (1900 г.) и Альбертом Эйнштейном адаптации концепции для объяснения фотоэлектрического эффекта (1905 г.) и до Эрвином Шредингером публикации его уравнение собственных функций в 1926 году, [1] концепция квантовых чисел, разработанная на основе атомной спектроскопии и теорий классической механики с дополнительными специальными ограничениями. [2] : 106 Многие результаты атомной спектроскопии были обобщены в формуле Ридберга, включающей разности между двумя рядами энергий, связанными целыми шагами. Модель атома , впервые предложенная Нильсом Бором в 1913 году, основывалась на одном квантовом числе. Вместе с ограничением Бора о том, что поглощение излучения не является классическим, это позволило объяснить связанную с рядом Бальмера . часть формулы атомного спектра Ридберга, [3]
Как отмечает Бор в своей последующей Нобелевской лекции, следующий шаг был сделан Арнольдом Зоммерфельдом в 1915 году. [4] В атомную модель Зоммерфельда добавлено второе квантовое число и концепция квантованных фазовых интегралов для их обоснования. [5] : 207 Модель Зоммерфельда все еще была по существу двумерной, моделируя электрон как движущийся по плоской орбите; в 1919 году он распространил свою работу на три измерения, используя «пространственное квантование» вместо квантованных фазовых интегралов. [6] : 152 Карл Шварцшильд и ученик Зоммерфельда Пол Эпштейн независимо друг от друга показали, что добавление третьего квантового числа дает полное объяснение результатов эффекта Штарка .
Следствием пространственного квантования стало то, что орбитальное взаимодействие электрона с внешним магнитным полем будет квантовано. Это, казалось, подтвердилось, когда в результатах эксперимента Штерна-Герлаха были получены результаты квантования атомов серебра в неоднородном магнитном поле. Подтверждение оказалось бы преждевременным: потребовалось бы больше квантовых чисел. [7]
Четвертое и пятое квантовые числа атомной эры возникли в результате попыток понять эффект Зеемана . Как и эксперимент Штерна-Герлаха, эффект Зеемана отражает взаимодействие атомов с магнитным полем; в слабом поле экспериментальные результаты были названы «аномальными», они расходились с любой теорией того времени. Вольфгангом Паули состояло в том, чтобы ввести еще одно квантовое число, принимающее только два возможных значения: Решение этой проблемы . [8] В конечном итоге это станет квантованными значениями проекции спина , собственного кванта углового момента электрона. В 1927 году Рональд Фрейзер продемонстрировал, что квантование в эксперименте Штерна-Герлаха было обусловлено магнитным моментом, связанным со спином электрона, а не его орбитальным угловым моментом. [7] Успех Паули в разработке аргументов в пользу спинового квантового числа без опоры на классические модели заложил основу для развития квантовых чисел элементарных частиц в оставшейся части 20-го века. [8]
Бор с его Aufbau , или принципом «наращивания», и Паули с его принципом исключения связали электронные квантовые числа атома с основой для предсказания свойств атомов. [9] Когда Шредингер опубликовал свое волновое уравнение и рассчитал энергетические уровни водорода, эти два принципа легли в основу атомной физики.
Ядерные квантовые числа
[ редактировать ]После успешных моделей атома внимание физики обратилось к моделям ядра. Начиная с первоначальной модели связи протон-нейтрон Гейзенберга в 1932 году, Юджин Вигнер в 1937 году ввел изоспин , первое «внутреннее» квантовое число, не связанное с симметрией в реальном пространстве-времени. [10] : 45
Связь с симметрией
[ редактировать ]По мере развития квантовой механики росла абстракция, и модели, основанные на симметрии и инвариантности, играли все большую роль. За два года до своей работы над квантовым волновым уравнением Шредингер применил идеи симметрии, выдвинутые Эмми Нётер и Германом Вейлем, к электромагнитному полю. [11] : 198 По мере развития квантовой электродинамики в 1930-х и 1940-х годах теория групп важным инструментом стала . К 1953 году Чэнь Нин Ян стал одержим идеей о том, что теорию групп можно применить для связи сохраняющихся квантовых чисел ядерных столкновений с симметриями в теории поля нуклонов. [11] : 202 Вместе с Робертом Миллсом Ян разработал неабелеву калибровочную теорию, основанную на сохранении квантовых чисел изоспина ядра .
Общие свойства
[ редактировать ]Хорошие квантовые числа соответствуют собственным значениям операторов , которые коммутируют с гамильтонианом , величинам, которые могут быть известны с точностью одновременно с энергией системы. В частности, наблюдаемые, которые коммутируют с гамильтонианом, одновременно диагонализуемы с ним, и поэтому собственные значения и энергия (собственные значения гамильтониана) не ограничены соотношением неопределенности, возникающим из-за некоммутативности. Вместе спецификация всех квантовых чисел квантовой системы полностью характеризует базовое состояние системы и в принципе может быть измерена вместе. Многие наблюдаемые в квантовой механике имеют дискретные спектры (наборы собственных значений) , поэтому величины можно измерять только в дискретных значениях. В частности, это приводит к квантовым числам, которые принимают значения в дискретных наборах целых или полуцелых чисел ; они могут приближаться к бесконечности хотя в некоторых случаях .
Подсчет квантовых чисел варьируется от системы к системе и не имеет универсального ответа. Следовательно, эти параметры необходимо найти для каждой анализируемой системы. Квантованная система требует хотя бы одного квантового числа. времени) любой квантовой системы описывается квантовым оператором в форме гамильтониана H Динамика (т.е. эволюция во . Существует одно квантовое число системы, соответствующее энергии системы; т. е. одно из собственных значений гамильтониана. Также существует одно квантовое число для каждого линейно независимого оператора O , коммутирующего с гамильтонианом. Полный набор коммутирующих наблюдаемых (CSCO), коммутирующих с гамильтонианом, характеризует систему со всеми ее квантовыми числами. Между квантовыми числами и операторами CSCO существует связь один к одному, при этом каждое квантовое число принимает одно из собственных значений соответствующего оператора. В результате разного базиса , который может быть произвольно выбран для формирования полного набора коммутирующих операторов, разные наборы квантовых чисел могут использоваться для описания одной и той же системы в разных ситуациях.
Электрон в водородоподобном атоме
[ редактировать ]описать энергетический уровень электрона в водородоподобном атоме Четыре квантовых числа могут полностью :
- Главное квантовое число ( n )
- Азимутальное квантовое число ( ℓ )
- Магнитное квантовое число ( м ℓ )
- Спиновое квантовое число ( м с )
Эти квантовые числа также используются в классическом описании состояний ядерных частиц (например, протонов и нейтронов). [ нужна ссылка ] Квантовое описание молекулярных орбиталей требует других квантовых чисел, поскольку симметрия молекулярной системы различна.
Главное квантовое число
[ редактировать ]Главное квантовое число описывает электронную оболочку электрона. Значение n варьируется от 1 до оболочки, содержащей самый внешний электрон этого атома, то есть [12]
- п = 1, 2, ...
Например, в цезии (Cs) самый внешний валентный электрон находится в оболочке с энергетическим уровнем 6, поэтому электрон в цезии может иметь значение n от 1 до 6. Среднее расстояние между электроном и ядром увеличивается с увеличением n .
Азимутальное квантовое число
[ редактировать ]Азимутальное квантовое число , также известное как квантовое число орбитального углового момента , описывает подоболочку и дает величину орбитального углового момента через соотношение
- л 2 = час 2 ℓ ( ℓ + 1).
В химии и спектроскопии ℓ = 0 называется s-орбиталью, ℓ = 1 — p-орбиталью, ℓ = 2 — d-орбиталью и ℓ = 3 — f-орбиталью.
Значение ℓ варьируется от 0 до n - 1 , поэтому первая p-орбиталь ( ℓ = 1 ) появляется во второй электронной оболочке ( n = 2 ), первая d-орбиталь ( ℓ = 2 ) появляется в третьей оболочке ( n = 3 ) и так далее: [13]
- ℓ = 0, 1, 2,..., п - 1
Квантовое число, начинающееся с n = 3, ℓ = 0, описывает электрон на s-орбитали третьей электронной оболочки атома. В химии это квантовое число очень важно, поскольку оно определяет форму атомной орбитали и сильно влияет на химические связи и валентные углы . Азимутальное квантовое число также может обозначать количество угловых узлов, присутствующих на орбитали. Например, для p-орбиталей ℓ = 1 , и, следовательно, количество угловых узлов на p-орбитали равно 1.
Магнитное квантовое число
[ редактировать ]Магнитное квантовое число описывает конкретную орбиталь внутри подоболочки и дает проекцию орбитального углового момента вдоль указанной оси :
- L z знак равно м ℓ час
Значения m ℓ варьируются от − ℓ до ℓ с целыми интервалами. [14] [ нужна страница ]
Подоболочка s ( ℓ = 0 ) содержит только одну орбиталь, и поэтому m ℓ электрона на s-орбитали всегда будет равна 0. Подоболочка p ( ℓ = 1 ) содержит три орбитали, поэтому m ℓ электрона в ap-орбиталь будет равна -1, 0 или 1. Подоболочка d ( ℓ = 2 ) содержит пять орбиталей со значениями m ℓ , равными -2, -1, 0, 1 и 2.
Спиновое магнитное квантовое число
[ редактировать ]Спиновое магнитное квантовое число описывает собственный спиновый угловой момент электрона внутри каждой орбитали и дает проекцию спинового углового момента S вдоль указанной оси:
- S z знак равно м s час .
В общем, значения m s варьируются от − s до s , где s — спиновое квантовое число, связанное с величиной собственного спинового углового момента частицы: [15]
- м s знак равно - s , - s + 1, - s + 2, ..., s - 2, s - 1, s .
Электронное состояние имеет спиновое число s = 1 / 2 , следовательно, m s будет + 1/2 « ( раскрутка») или - 1/2 со состояния «спином вниз». Поскольку электрон является фермионом, он подчиняется принципу запрета Паули : каждое электронное состояние должно иметь разные квантовые числа. Следовательно, каждая орбиталь будет занята не более чем двумя электронами, по одному на каждое спиновое состояние.
Принцип Ауфбау и правила Хунда.
[ редактировать ]Многоэлектронный атом можно качественно смоделировать как водородоподобный атом с более высоким зарядом ядра и, соответственно, большим количеством электронов. Заселенность электронных состояний в таком атоме можно предсказать с помощью принципа Ауфбау и эмпирических правил Хунда для квантовых чисел. Принцип Ауфбау заполняет орбитали на основе их главного и азимутального квантовых чисел (самое низкое сначала с наименьшим разрыв связей; Правило Хунда отдает предпочтение неспаренным электронам на самой внешней орбитали). Эти правила являются эмпирическими, но их можно отнести к электронной физике. [16] : 10 [17] : 260
Спин-орбитальные связанные системы
[ редактировать ]Если принять во внимание спин-орбитальное взаимодействие , операторы L и S больше не коммутируют с гамильтонианом , а собственные состояния системы больше не имеют четко определенных орбитальных угловых моментов и спинов. Таким образом, следует использовать другой набор квантовых чисел. В этот набор входят [18] [19]
- Квантовое число полного углового момента :
- j = | ℓ ± с |
что дает полный угловой момент через соотношение
- Дж 2 = час 2 j ( д + 1)
- Проекция полного момента импульса на заданную ось:
- м j = - j , - j + 1, - j + 2, ..., j - 2, j - 1, j
аналогично предыдущему и удовлетворяет
- м j знак равно м ℓ + м с и | м ℓ + м с | ≤ j
- Паритет
Это собственное значение отражаемое : положительное (+1) для состояний, пришедших из четного ℓ , и отрицательное (-1) для состояний, пришедших из нечетного ℓ . Первый также известен как четность , а второй как нечетность и определяется выражением
- Р = (−1) ℓ
Например, рассмотрим следующие 8 состояний, определяемых их квантовыми числами:
н ℓ м ℓ РС ℓ + с ℓ - с м ℓ + м с (1) 2 1 1 + 1 / 2 3 / 2 1 / 2 3 / 2 (2) 2 1 1 − 1 / 2 3 / 2 1 / 2 1 / 2 (3) 2 1 0 + 1 / 2 3 / 2 1 / 2 1 / 2 (4) 2 1 0 − 1 / 2 3 / 2 1 / 2 − 1 / 2 (5) 2 1 −1 + 1 / 2 3 / 2 1 / 2 − 1 / 2 (6) 2 1 −1 − 1 / 2 3 / 2 1 / 2 − 3 / 2 (7) 2 0 0 + 1 / 2 1 / 2 − 1 / 2 1 / 2 (8) 2 0 0 − 1 / 2 1 / 2 − 1 / 2 − 1 / 2
Квантовые состояния в системе можно описать как линейную комбинацию этих восьми состояний. Однако при наличии спин-орбитального взаимодействия , если мы хотим описать одну и ту же систему 8 состояниями, которые являются ( т.е. собственными векторами гамильтониана каждое представляет собой состояние, которое не смешивается с другими с течением времени), нам следует рассмотреть следующие 8 говорится:
дж м дж паритет 3 / 2 3 / 2 странный исходя из состояния (1) выше 3 / 2 1 / 2 странный исходящие из состояний (2) и (3) выше 3 / 2 − 1 / 2 странный исходящие из состояний (4) и (5) выше 3 / 2 − 3 / 2 странный исходя из состояния (6) выше 1 / 2 1 / 2 странный исходящие из состояний (2) и (3) выше 1 / 2 − 1 / 2 странный исходящие из состояний (4) и (5) выше 1 / 2 1 / 2 даже исходя из состояния (7) выше 1 / 2 − 1 / 2 даже исходя из состояния (8) выше
Атомные ядра
[ редактировать ]В ядрах вся совокупность протонов и нейтронов ( нуклонов ) имеет результирующий угловой момент, обусловленный угловыми моментами каждого нуклона, обычно I. обозначаемый Если полный угловой момент нейтрона равен j n = ℓ + s , а для протона j p = ℓ + s (где s для протонов и нейтронов равен 1/2 : см снова ( . примечание )), тогда квантовые числа ядерного углового момента I определяются по формуле
- я = | j n - j п |, | j п - j п | + 1, | j п - j п | + 2, ..., ( j n + j п ) - 2, ( j n + j п ) - 1, ( j n + j п )
Примечание. Все орбитальные угловые моменты ядерных (и атомных) состояний кратны ħ, а собственные угловые моменты нейтрона и протона кратны полуцелому числу. Должно быть сразу очевидно, что комбинация собственных спинов нуклонов с их орбитальным движением всегда будет давать полуцелые значения полного спина I любого ядра с нечетным А и целые значения для любого ядра с четным А.
Четность с числом I используется для обозначения состояний ядерного углового момента, примерами некоторых изотопов водорода (H), углерода (C) и натрия (Na); [20]
1
1 часЯ = ( 1 / 2 ) + 9
6 СЯ = ( 3 / 2 ) − 20
11 Ная = 2 + 2
1 чася = 1 + 10
6 Ся = 0 + 21
11 НаЯ = ( 3 / 2 ) + 3
1 часЯ = ( 1 / 2 ) + 11
6 СЯ = ( 3 / 2 ) − 22
11 Ная = 3 + 12
6 Ся = 0 + 23
11 НаЯ = ( 3 / 2 ) + 13
6 СЯ = ( 1 / 2 ) − 24
11 Ная = 4 + 14
6 Ся = 0 + 25
11 НаЯ = ( 5 / 2 ) + 15
6 СЯ = ( 1 / 2 ) + 26
11 Ная = 3 +
Причина необычных флуктуаций I , даже из-за разницы всего в один нуклон, связана с нечетным и четным числом протонов и нейтронов - пары нуклонов имеют нулевой общий угловой момент (так же, как электроны на орбиталях), оставляя нечетное или четное число неспаренных нуклонов. Свойство ядерного спина является важным фактором для работы ЯМР- спектроскопии в органической химии . [19] и МРТ в ядерной медицине , [20] за счет ядерного магнитного момента, взаимодействующего с внешним магнитным полем .
Элементарные частицы
[ редактировать ]Элементарные частицы содержат множество квантовых чисел, которые обычно считаются присущими им. Однако следует понимать, что элементарные частицы представляют собой квантовые состояния стандартной модели физики элементарных частиц , и, следовательно, квантовые числа этих частиц имеют такое же отношение к гамильтониану этой модели, как квантовые числа атома Бора к его Гамильтониан . Другими словами, каждое квантовое число обозначает симметрию задачи. полезнее В квантовой теории поля различать пространство-время и внутреннюю симметрию.
Типичными квантовыми числами, связанными с симметрией пространства-времени , являются спин (связанный с вращательной симметрией), четность , C-четность и T-четность (связанный с симметрией Пуанкаре пространства -времени ). Типичные внутренние симметрии [ нужны разъяснения ] лептонное число и барионное число или электрический заряд . (Полный список таких квантовых чисел см. в статье о вкусе .)
Мультипликативные квантовые числа
[ редактировать ]Большинство консервативных квантовых чисел аддитивны, поэтому в реакции элементарных частиц сумма квантовых чисел должна быть одинаковой до и после реакции. Однако некоторые из них, обычно называемые четностью , являются мультипликативными; т. е. их продукт сохраняется. Все мультипликативные квантовые числа принадлежат к симметрии (например, к четности), при которой применение преобразования симметрии дважды эквивалентно бездействию ( инволюция ).
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Шрёдингер, Эрвин (1926). «Квантование как проблема собственных значений». Аннален дер Физик . 81 (18): 109–139. Бибкод : 1926АнП...386..109С . дои : 10.1002/andp.19263861802 .
- ^ Уиттакер, Эдмунд Т. (1989). История теорий эфира и электричества. 2: Современные теории, 1900–1926 гг. (Ред.). Нью-Йорк: Dover Publ. ISBN 978-0-486-26126-3 .
- ^ Хейлброн, Джон Л. (июнь 2013 г.). «Путь к квантовому атому» . Природа . 498 (7452): 27–30. дои : 10.1038/498027a . ISSN 0028-0836 . ПМИД 23739408 .
- ^ Нильс Бор – Нобелевская лекция . Нобелевская премия.org. Нобелевская премия AB 2024. Вс. 25 февраля 2024 г.
- ^ Эккерт, Майкл; Эккерт, Майкл; Артин, Том (2013). Арнольд Зоммерфельд: наука, жизнь и неспокойные времена 1868-1951 гг . Нью-Йорк: Спрингер. ISBN 978-1-4614-7461-6 .
- ^ Краг, Хельге (17 мая 2012 г.). Нильс Бор и квантовый атом: модель атомной структуры Бора 1913–1925 гг . Издательство Оксфордского университета. doi : 10.1093/acprof:oso/9780199654987.003.0004 . ISBN 978-0-19-965498-7 .
- ^ Перейти обратно: а б Фридрих, Бретислав; Хершбах, Дадли (1 декабря 2003 г.). «Штерн и Герлах: как плохая сигара помогла переориентировать атомную физику» . Физика сегодня . 56 (12): 53–59. Бибкод : 2003ФТ....56л..53Ф . дои : 10.1063/1.1650229 . ISSN 0031-9228 .
- ^ Перейти обратно: а б Джулини, Доменико (1 сентября 2008 г.). «Электронный спин или «классически неописуемая двузначность» » . Исследования по истории и философии науки. Часть B: Исследования по истории и философии современной физики . 39 (3): 557–578. arXiv : 0710.3128 . Бибкод : 2008ШПМП..39..557Г . дои : 10.1016/j.shpsb.2008.03.005 . hdl : 11858/00-001M-0000-0013-13C8-1 . ISSN 1355-2198 .
- ^ Краг, Хельге (17 мая 2012 г.). Нильс Бор и квантовый атом: модель атомной структуры Бора 1913–1925 гг . Издательство Оксфордского университета. doi : 10.1093/acprof:oso/9780199654987.003.0007 . ISBN 978-0-19-965498-7 .
- ^ Браун, LM (1988). «Замечания по истории изоспина» . Зимой, Клаус; Телегди, Валентин Л. (ред.). Фести-Вал: Фестиваль Вал Телегди; сочинения по физике в честь своего 65-летия; [симпозиум... состоялся в ЦЕРН, Женева, 6 июля 1987 г.] . Амстердам: Физическое издательство Северной Голландии. ISBN 978-0-444-87099-5 .
- ^ Перейти обратно: а б Бэгготт, Дж. Э. (2013). Квантовая история: история за 40 мгновений (Впечатление: 3-е изд.). Оксфорд: Оксфордский университет. Нажимать. ISBN 978-0-19-956684-6 .
- ^ Бейзер, А. (1987). Концепции современной физики (4-е изд.). МакГроу-Хилл (международный). ISBN 0-07-100144-1 . [ нужна страница ]
- ^ Аткинс, PW (1977). Молекулярная квантовая механика, части I и II: Введение в квантовую химию . Том. 1. Издательство Оксфордского университета. ISBN 0-19-855129-0 . [ нужна страница ]
- ^ Айсберг и Резник 1985 .
- ^ Пелег, Ю.; Пнини, Р.; Заарур, Э.; Хехт, Э. (2010). Квантовая механика . Очерки Шуама (2-е изд.). МакГроу Хилл (США). ISBN 978-0-07-162358-2 . [ нужна страница ]
- ^ Джолли, Уильям Л. (1984). Современная неорганическая химия (1-е изд.). МакГроу-Хилл. стр. 10–12 . ISBN 0-07-032760-2 .
- ^ Левин, Ира Н. (1983). Физическая химия (2-е изд.). Нью-Йорк: МакГроу-Хилл. ISBN 978-0-07-037421-8 .
- ^ Аткинс, PW (1977). Молекулярная квантовая механика, части I и II: Введение в квантовую химию . Том. 1. Издательство Оксфордского университета. ISBN 0-19-855129-0 . [ нужна страница ]
- ^ Перейти обратно: а б Аткинс, PW (1977). Молекулярная квантовая механика. Часть III: Введение в квантовую химию . Том. 2. Издательство Оксфордского университета. [ ISBN отсутствует ] [ нужна страница ]
- ^ Перейти обратно: а б Крейн, Канзас (1988). Введение в ядерную физику . Джон Уайли и сыновья. ISBN 978-0-471-80553-3 . [ нужна страница ]
Дальнейшее чтение
[ редактировать ]- Дирак, Поль AM (1982). Принципы квантовой механики . Издательство Оксфордского университета. ISBN 0-19-852011-5 .
- Гриффитс, Дэвид Дж. (2004). Введение в квантовую механику (2-е изд.). Прентис Холл. ISBN 0-13-805326-Х .
- Халзен, Фрэнсис и Мартин, Алан Д. (1984). Кварки и лептоны: вводный курс в современную физику элементарных частиц . Джон Уайли и сыновья. ISBN 0-471-88741-2 .
- Айсберг, Роберт Мартин; Резник, Роберт (1985). Квантовая физика атомов, молекул, твердых тел, ядер и частиц (2-е изд.). Джон Уайли и сыновья. ISBN 978-0-471-87373-0 – через Интернет-архив .




