Псевдонимы

Эта статья посвящена псевдонимам при обработке сигналов, включая компьютерную графику. Чтобы получить доступ к одним и тем же данным с использованием разных имен в компьютерном программировании, см. Псевдонимы (вычисления) .

Пример псевдонимов

Это полноразмерное изображение показывает, как должно выглядеть правильно сэмплированное изображение кирпичной стены на экране достаточного разрешения .

При уменьшении разрешения появляется алиасинг в виде муарового узора .

Движение «камеры» с постоянной выдержкой создает временное сглаживание, известное как эффект колеса телеги . Скорость «камеры», движущейся вправо, постоянно увеличивается с той же скоростью, что и объекты, скользящие влево. В середине 24-секундного цикла кажется, что объекты внезапно смещаются и направляются в обратном направлении, вправо.

В обработке сигналов и смежных дисциплинах наложение спектров — это перекрытие частотных составляющих, возникающее в результате частоты дискретизации ниже частоты Найквиста . Это перекрытие приводит к искажениям или артефактам при восстановлении сигнала из выборок, что приводит к тому, что восстановленный сигнал отличается от исходного непрерывного сигнала.Сглаживание, возникающее в сигналах, дискретизированных во времени, например, в цифровом аудио или стробоскопическом эффекте , называется временным сглаживанием . Сглаживание в пространственно дискретизированных сигналах (например, муаровых узорах в цифровых изображениях ) называется пространственным сглаживанием .

Наложения спектров обычно можно избежать, применяя фильтры нижних частот или фильтры сглаживания (AAF) к входному сигналу перед дискретизацией и при преобразовании сигнала с более высокой частоты дискретизации на более низкую. Затем следует использовать подходящую восстанавливающую фильтрацию при восстановлении дискретизированного сигнала в непрерывной области или преобразовании сигнала с более низкой частоты дискретизации на более высокую. Для пространственного сглаживания типы сглаживания включают быстрое приблизительное сглаживание (FXAA), многосэмпловое сглаживание и суперсэмплинг .

Описание

Точки на небе из-за пространственного сглаживания, вызванного изменением размера полутонов до более низкого разрешения.

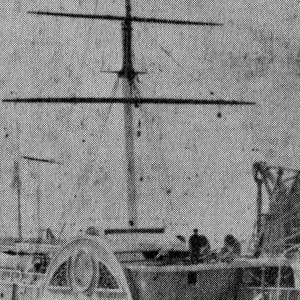
При просмотре цифрового изображения реконструкция выполняется с помощью дисплея или принтера, а также глаз и мозга. Если данные изображения обрабатываются неправильно во время выборки или реконструкции, восстановленное изображение будет отличаться от исходного изображения и будет виден псевдоним.

Примером пространственного наложения является муар, наблюдаемый на плохо пикселизированном изображении кирпичной стены. Методы пространственного сглаживания позволяют избежать такой плохой пикселизации. Алиасинг может быть вызван либо стадией выборки, либо стадией реконструкции; их можно отличить, назвав сглаживание выборки предварительным псевдонимом и псевдоним реконструкции посталиасингом.

Временное сглаживание является серьезной проблемой при дискретизации видео- и аудиосигналов. Музыка, например, может содержать высокочастотные компоненты, неслышимые для человека. Если музыкальное произведение сэмплируется с частотой 32 000 выборок в секунду или выше (Гц), любые частотные компоненты на уровне 16 000 Гц ( частота Найквиста для этой частоты дискретизации) вызовут наложение спектров, когда музыка воспроизводится цифро-аналоговым преобразователем ( ЦАП). Высокие частоты аналогового сигнала будут отображаться как более низкие частоты (неправильный псевдоним) в записанном цифровом сэмпле и, следовательно, не могут быть воспроизведены ЦАП. Чтобы предотвратить это, фильтр сглаживания, перед выборкой используется который удаляет компоненты выше частоты Найквиста.

В видео или кинематографии временное сглаживание возникает из-за ограниченной частоты кадров и вызывает эффект колеса повозки , при котором кажется, что колесо со спицами вращается слишком медленно или даже назад. Алиасинг изменил видимую частоту вращения. Изменение направления можно описать как отрицательную частоту . Частоты временных наложений в видео и кинематографии определяются частотой кадров камеры, но относительная интенсивность наложенных частот определяется временем срабатывания затвора (временем экспозиции) или использованием фильтра уменьшения временных наложений во время съемок.

Как и видеокамера, большинство схем выборки являются периодическими; то есть они имеют характерную частоту дискретизации во времени или в пространстве. Цифровые камеры предоставляют определенное количество образцов ( пикселей ) на градус или радиан, или образцов на мм в фокальной плоскости камеры. Аудиосигналы дискретизируются ( оцифровываются ) с помощью аналого-цифрового преобразователя , который производит постоянное количество выборок в секунду. Некоторые из наиболее ярких и тонких примеров наложения спектров возникают, когда дискретизируемый сигнал также имеет периодическое содержание.

Функции с ограниченным диапазоном частот

Основная статья: Теорема выборки Найквиста – Шеннона

Реальные сигналы имеют конечную длительность, а их частотный состав, определенный преобразованием Фурье , не имеет верхней границы. При выборке таких функций всегда происходит некоторое количество псевдонимов. Функции, частотное содержание которых ограничено ( ограничено полосой пропускания ), имеют бесконечную продолжительность во временной области. Если выборка производится с достаточно высокой частотой, определяемой полосой пропускания , исходная функция теоретически может быть идеально восстановлена ​​из бесконечного набора выборок.

Полосовые сигналы

Основная статья: Недостаточная выборка

Иногда наложение псевдонимов намеренно используется для сигналов без низкочастотного содержания, называемых полосовыми сигналами. Недостаточная дискретизация , которая создает низкочастотные псевдонимы, может дать тот же результат с меньшими усилиями, что и сдвиг частоты сигнала в сторону более низких частот перед дискретизацией с более низкой частотой. Некоторые цифровые преобразователи каналов таким образом используют псевдонимы для повышения эффективности вычислений.  (См. Выборка (обработка сигнала) , Частота Найквиста (относительно выборки) и Банк фильтров .)

Выборка синусоидальных функций

Рис.2 Вверху слева: Анимация изображает последовательность синусоид, каждая из которых имеет более высокую частоту, чем предыдущие. Эти «истинные» сигналы также дискретизируются (синие точки) с постоянной частотой/скоростью. $f_{s}.$
Вверху справа: непрерывное . преобразование Фурье синусоиды (не выборок) Единственный ненулевой компонент, отображающий фактическую частоту, означает отсутствие двусмысленности.
Внизу справа: дискретное . преобразование Фурье только доступных выборок Наличие двух компонентов означает, что образцы могут соответствовать как минимум двум разным синусоидам, одна из которых является истинной частотой (вверху справа).
Внизу слева: используя те же выборки (теперь они выделены оранжевым цветом), алгоритм реконструкции по умолчанию создает низкочастотную синусоиду.

Синусоиды являются важным типом периодической функции, поскольку реалистичные сигналы часто моделируются как сумма множества синусоид разных частот и разных амплитуд (например, с помощью ряда Фурье или преобразования ). Понимание того, что сглаживание делает с отдельными синусоидами, полезно для понимания того, что происходит с их суммой.

При дискретизации функции на частоте f _s (интервалы 1/ f _s ) следующие функции времени ( t ) дают одинаковые наборы выборок: {sin(2π( f+Nf _s ) t + φ), N = 0, ± 1, ±2, ±3,... }. Частотный спектр образцов дает одинаково сильные отклики на всех этих частотах. Без дополнительной информации частота исходной функции неоднозначна. Поэтому говорят, что функции и их частоты являются псевдонимами друг друга. Учитывая тригонометрическое тождество :

$\sin(2\pi (f+Nf_{\rm {s}})t+\phi )=\left\{{\begin{array}{ll}+\sin(2\pi (f+Nf_{\rm {s}})t+\phi ),&f+Nf_{\rm {s}}\geq 0\\-\sin(2\pi |f+Nf_{\rm {s}}|t-\phi ),&f+Nf_{\rm {s}}<0\\\end{array}}\right.$

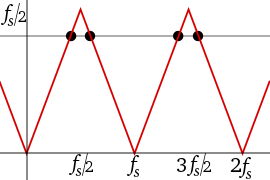
мы можем записать все частоты псевдонимов как положительные значения: $f_{_{N}}(f)\triangleq \left|f+Nf_{\rm {s}}\right|$. Например, снимок нижнего правого кадра рис.2 показывает компонент на фактической частоте. $f$ и еще один компонент по псевдониму $f_{_{-1}}(f)$. Как $f$ увеличивается во время анимации, $f_{_{-1}}(f)$ уменьшается. Точка, в которой они равны $(f=f_{s}/2)$ представляет собой ось симметрии, называемую частотой сгиба , также известной как частота Найквиста .

Псевдонимы имеют значение, когда кто-то пытается восстановить исходную форму сигнала по его выборкам. Самый распространенный метод реконструкции позволяет получить наименьшие из $f_{_{N}}(f)$ частоты. Поэтому обычно важно, чтобы $f_{0}(f)$ быть уникальным минимумом. Необходимым и достаточным условием для этого является $f_{s}/2>|f|,$ называется условием Найквиста . В левом нижнем кадре рис.2 изображен типичный результат реконструкции имеющихся образцов. До $f$ превышает частоту Найквиста, реконструкция соответствует фактической форме сигнала (верхний левый кадр). После этого это низкочастотный псевдоним верхнего кадра.

Складной

На рисунках ниже представлены дополнительные изображения псевдонимов из-за выборки. График зависимости амплитуды от частоты (не времени) для одиночной синусоиды на частоте и некоторых _как ее псевдонимов на частотах , 1,4 _фс фс   и 1,6 _фс фс 0,4 будет выглядеть _0,6 4 черные точки на рис.3. Красные линии изображают пути ( локусы ) четырех точек, если бы мы отрегулировали частоту и амплитуду синусоиды вдоль сплошного красного сегмента (между f _s /2 и f _s ). Независимо от того, какую функцию мы выберем для изменения амплитуды в зависимости от частоты, график будет демонстрировать симметрию между 0 и f _s . Складывание часто наблюдается на практике при просмотре частотного спектра вещественных отсчетов, например, на рис.4.

Рис.3: Черные точки являются псевдонимами друг друга. Сплошная красная линия — пример изменения амплитуды в зависимости от частоты. Пунктирные красные линии — это соответствующие пути псевдонимов.

Рис.4: Преобразование Фурье музыки, дискретизированной с частотой 44 100 выборок в секунду, демонстрирует симметрию (так называемую «складку») вокруг частоты Найквиста (22 050 Гц).

Рис.5: График наложения частот, показывающий частоту и периодичность сворачивания. Частоты выше f s /2 имеют псевдоним ниже f s /2, значение которого указано на этом графике.

Две сложные синусоиды, окрашенные в золотой и голубой цвета, которые соответствуют одним и тем же наборам реальных и воображаемых точек выборки при выборке со скоростью ( f _s ), указанной линиями сетки. Показанный здесь случай: f _cyan = f ₋₁ ( f _gold ) = f _gold – f _s

Сложные синусоиды

Сложные синусоиды — это сигналы, образцы которых представляют собой комплексные числа концепция отрицательной частоты , и для их различения необходима . В этом случае частоты псевдонимов задаются просто :   f _N ( f ) = f + N f _s . Следовательно, по мере f увеличения от 0 до f _s ,   f ₋₁ ( f ) также увеличивается (от – f _s до 0). Следовательно, сложные синусоиды не имеют складок .

Частота выборки

Иллюстрация четырех сигналов, восстановленных на основе образцов, взятых с шестью различными скоростями. Два сигнала достаточно дискретизированы, чтобы избежать наложений на всех шести скоростях. Два других иллюстрируют увеличение искажений (алиасинга) при более низких скоростях.

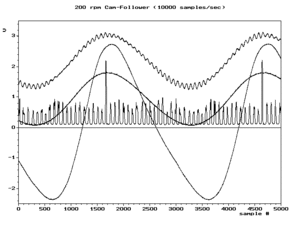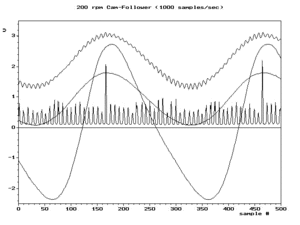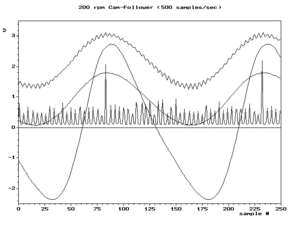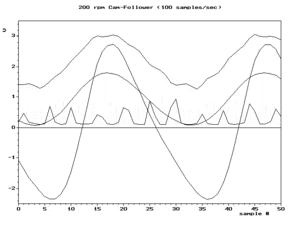
Когда условие f _s /2 > f выполняется для самой высокочастотной составляющей исходного сигнала, то оно выполняется и для всех частотных составляющих, это условие называется критерием Найквиста . Обычно это аппроксимируется путем фильтрации исходного сигнала для ослабления высокочастотных составляющих перед его дискретизацией. Эти ослабленные высокочастотные компоненты по-прежнему создают низкочастотные помехи, но обычно с достаточно низкими амплитудами, чтобы не вызывать проблем. Фильтр, выбранный с учетом определенной частоты дискретизации, называется фильтром сглаживания .

Отфильтрованный сигнал впоследствии может быть восстановлен с помощью алгоритмов интерполяции без значительных дополнительных искажений. Большинство дискретизированных сигналов не просто сохраняются и реконструируются. Но точность теоретической реконструкции (с помощью интерполяционной формулы Уиттекера-Шеннона ) является обычной мерой эффективности выборки.

Историческое использование

Исторически термин «алиасинг» возник из радиотехники из-за действия супергетеродинных приемников . Когда приемник смещает несколько сигналов вниз на более низкие частоты, с ВЧ на ПЧ посредством гетеродинирования , нежелательный сигнал с РЧ частоты находится на таком же расстоянии от частоты гетеродина (LO), что и полезный сигнал, но на неправильной стороне гетеродинного сигнала. может оказаться на той же частоте ПЧ, что и желаемая. Если он достаточно сильный, он может помешать приему желаемого сигнала. Этот нежелательный сигнал известен как изображение или псевдоним полезного сигнала.

Первое письменное использование терминов «псевдоним» и «наложение псевдонимов» в обработке сигналов, по-видимому, встречается в неопубликованном техническом меморандуме Bell Laboratories 1949 года. и Джон Тьюки Ричард Хэмминг . Эта статья включает пример совмещения частот, датируемый 1922 годом. Первое опубликованное использование термина «сглаживание» в этом контексте принадлежит Блэкману и Тьюки в 1958 году. В предисловии к переизданию Dover В этой статье они отмечают, что идея псевдонимов была графически проиллюстрирована Штумпфом. десятью годами ранее.

В техническом отчете Bell 1949 года псевдонимы упоминаются как общеизвестная концепция, но не приводится источник этого термина. Гвилим Дженкинс и Морис Пристли благодарны Тьюки за то, что он представил его в этом контексте: хотя аналогичная концепция псевдонимов была введена несколькими годами ранее в дробных факторных планах . В то время как Тьюки проделал значительную работу в факторных экспериментах и, конечно же, знал о псевдонимах в дробных конструкциях, невозможно определить, было ли сознательное использование им «алиасинга» при обработке сигналов такими замыслами.

Угловое сглаживание

Наложение псевдонимов происходит всякий раз, когда использование дискретных элементов для захвата или создания непрерывного сигнала приводит к неопределенности частоты.

Пространственное сглаживание, в частности угловой частоты, может возникать при воспроизведении светового поля или звукового поля с дискретными элементами, как в 3D-дисплеях или волнового поля . синтезе звука

Это сглаживание видно на таких изображениях, как плакаты с лентикулярной печатью : если они имеют низкое угловое разрешение, то при движении мимо них, скажем, слева направо, 2D-изображение изначально не меняется (поэтому кажется, что оно движется влево). , то при переходе к следующему угловому изображению изображение внезапно меняется (поэтому оно прыгает вправо) – и частота и амплитуда этого движения из стороны в сторону соответствуют угловому разрешению изображения (а для частоты скорость бокового движения зрителя), что представляет собой угловое сглаживание 4D светового поля.

Отсутствие параллакса при движении зрителя в 2D-изображениях и в 3D-фильмах, снятых с помощью стереоскопических очков (в 3D-фильмах эффект называется « рысканием », поскольку изображение вращается вокруг своей оси) аналогичным образом можно рассматривать как потерю углового эффекта. разрешение, при этом все угловые частоты приравниваются к 0 (постоянному).

Еще примеры

Аудио пример

Качественные эффекты наложения псевдонимов можно услышать в следующей аудиодемонстрации. Шесть пилообразных волн воспроизводятся последовательно: первые две пилообразные имеют основную частоту 440 Гц (А4), вторые две имеют основную частоту 880 Гц (А5) и последние две - 1760 Гц (А6). Пилообразные сигналы чередуются между с ограниченной полосой пропускания пилообразными (без наложения) и пилообразными с наложением, а частота дискретизации составляет 22050 Гц. Пилообразные сигналы с ограниченной полосой частот синтезируются из ряда Фурье пилообразных сигналов так, что гармоники выше частоты Найквиста отсутствуют.

Алиасинговые искажения на нижних частотах становятся все более очевидными с более высокими основными частотами, и хотя пилообразная форма с ограниченной полосой частот все еще ясна на частоте 1760 Гц, совмещенная пилообразная форма ухудшается и становится резкой, а на частотах ниже основной частоты слышно жужжание.

Пеленгация

Форма пространственного наложения может также возникать в антенных решетках или микрофонных решетках, используемых для оценки направления прихода волнового сигнала, как, например, при геофизических исследованиях сейсмическими волнами. Волны должны отбираться с большей плотностью, чем две точки на длину волны , иначе направление прихода волны станет неоднозначным.

См. также

• Зона Бриллюэна
• Словарь видеотерминов
• Джегги
• Фактор Келла
• Синк-фильтр
• Функция Sinc
• Спектральная плотность
• Спектральная утечка
• Стробоскопический эффект
• Эффект колеса телеги
• Теорема выборки Найквиста – Шеннона § Критическая частота

Дальнейшее чтение

• Фарр, Мэтт ; Хамфрис, Грег. (28 июня 2010 г.). Физически обоснованный рендеринг: от теории к реализации . Морган Кауфманн . ISBN   978-0-12-375079-2 . Глава 7 ( Выборка и реконструкция ) . Проверено 3 марта 2013 г.

Внешние ссылки

• Сглаживание с помощью дискретного осциллографа на YouTube, автор Tektronix Application Engineer
• Праймер для сглаживающего фильтра от La Vida Leica, обсуждает его назначение и влияние на записанные изображения.
• Интерактивные примеры, демонстрирующие эффект псевдонимов