Простая ячейка
| Простая ячейка | |
|---|---|
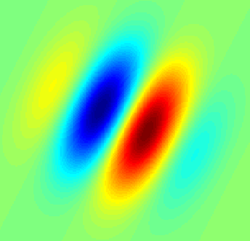 Рецептивное поле типа фильтра Габора, типичное для простой клетки. Синие области указывают на торможение, красные на облегчение. | |
| Подробности | |
| Часть | первичная зрительная кора |
| Система | Визуальная система |
| Анатомическая терминология | |
Простая клетка первичной зрительной коры — это клетка, которая реагирует преимущественно на ориентированные края и решетки (полоски определенной ориентации). Эти клетки были открыты Торстеном Визелем и Дэвидом Хьюбелом в конце 1950-х годов. [1]
Такие ячейки настраиваются на разные частоты и ориентации, даже с разными фазовыми соотношениями, возможно, для извлечения информации о несоответствии (глубине) и для присвоения глубины обнаруженным линиям и краям. [2] Это может привести к созданию трехмерного «каркасного» представления, используемого в компьютерной графике. Тот факт, что входные данные от левого и правого глаза очень близки в так называемых кортикальных гиперколонках, указывает на то, что глубинная обработка происходит на очень ранней стадии, помогая распознавать трехмерные объекты.
Позже было обнаружено множество других ячеек со специфическими функциями: (а) ячейки с остановленными концами, которые, как полагают, обнаруживают особенности, такие как пересечения линий и ребер, вершины и окончания линий; (б) стержневые и решетчатые ячейки . Последние не являются линейными операторами, поскольку стержневая ячейка не реагирует, увидев стержень, являющийся частью периодической решетки, а ячейка решетки не реагирует, увидев изолированный стержень.
Используя математическую модель Габора с синусоидальными и косинусными компонентами (фазами), затем моделируются сложные ячейки путем вычисления модуля комплексных ответов Габора. Как простые, так и сложные ячейки являются линейными операторами и рассматриваются как фильтры, поскольку избирательно реагируют на большое количество шаблонов.
Однако утверждалось, что модель Габора не соответствует анатомической структуре зрительной системы, поскольку она сокращает LGN и использует 2D-изображение, проецируемое на сетчатку . Аззопарди и Петков [3] предложили вычислительную модель простой клетки, которая сочетает в себе реакции модельных клеток LGN с центрально-окружающими рецептивными полями (RF). Они называют это моделью комбинации РФ (CORF). Помимо избирательности ориентации, он демонстрирует подавление перекрестной ориентации , настройку контрастной инвариантной ориентации и насыщение реакции. Эти свойства наблюдаются в реальных простых ячейках, но не присущи модели Габора . Используя моделирование обратной корреляции, они также демонстрируют, что RF- карта модели CORF может быть разделена на удлиненные возбуждающие и тормозные области, типичные для простых клеток.
Линдеберг [4] [5] вывел аксиоматически определенные модели простых ячеек в терминах производных по направлению аффинных гауссовских ядер во временной области в сочетании с временными производными либо непричинных, либо причинно-временных ядер масштабного пространства во временной области и показал, что эта теория одновременно ведет к к предсказаниям о рецептивных полях с хорошим качественным согласием с измерениями биологических рецептивных полей, выполненными DeAngelis et al. [6] [7] и гарантирует хорошие теоретические свойства математической модели рецептивного поля, включая свойства ковариации и инвариантности при естественных преобразованиях изображений. [8] [9]
История [ править ]
Эти клетки были открыты Торстеном Визелем и Дэвидом Хьюбелом в конце 1950-х годов. [10]
Хьюбель и Визель назвали эти клетки «простыми», в отличие от « сложных клеток », потому что у них были общие свойства: [11]
- Они имеют отдельные возбуждающие и тормозные области.
- Эти регионы следуют свойству суммирования.
- Эти области имеют взаимный антагонизм — возбуждающие и тормозные участки уравновешиваются при рассеянном освещении.
- По карте возбуждающих и тормозных областей можно предсказать реакцию на движущиеся стимулы.
Некоторые другие исследователи, такие как Питер Бишоп и Питер Шиллер, использовали разные определения простых и сложных клеток. [12]
Ссылки [ править ]
- ^ Д. Х. Хьюбел и Т. Н. Визель Рецептивные поля одиночных нейронов в полосатой коре головного мозга кошки J. Physiol. стр. 574-591 (148) 1959 г.
- ^ Фриман, РД; ДеАнджелис, GC; Одзава, И. (31 августа 1990 г.). «Стереоскопическая распознавание глубины в зрительной коре: нейроны идеально подходят в качестве детекторов несоответствия». Наука . 249 (4972): 1037–1041. Бибкод : 1990Sci...249.1037O . CiteSeerX 10.1.1.473.8284 . дои : 10.1126/science.2396096 . ISSN 1095-9203 . ПМИД 2396096 .
- ^ Г. Аззопарди и Н. Петков Вычислительная модель CORF, основанная на входных данных LGN, превосходит модель функции Габора Biological Cybernetics, vol. 106(3), стр. 177–189, DOI: 10.1007/s00422-012-0486-6, 2012 г.
- ^ Т. Линдеберг «Вычислительная теория зрительных рецептивных полей», Биологическая кибернетика 107 (6): 589-635, 2013
- ^ Т. Линдеберг «Нормативная теория зрительных рецептивных полей», Heliyon 7 (1): e05897, 2021.
- ^ GC DeAngelis, I. Ohzawa и RD Freeman «Динамика рецептивного поля в центральных зрительных путях». Тенденции Неврологии. 18(10), 451–457, 1995.
- ^ GC DeAngelis и A. Anzai «Современный взгляд на классическое рецептивное поле: линейная и нелинейная пространственно-временная обработка нейронами V1. В: Чалупа, Л.М., Вернер, Дж.С. (ред.) The Visual Neurosciences, том 1 , стр. 704–719. MIT Press, Кембридж, 2004.
- ^ Т. Линдеберг «Инвариантность зрительных операций на уровне рецептивных полей», PLOS ONE 8 (7): e66990, страницы 1–33, 2013 г.
- ^ Т. Линдеберг «Ковариационные свойства при естественных преобразованиях изображений для обобщенной модели производной Гаусса для зрительных рецептивных полей», Frontiers in Computational Neuroscience, 17:1189949, 2023.
- ^ Д. Х. Хьюбел и Т. Н. Визель Рецептивные поля одиночных нейронов в полосатой коре головного мозга кошки J. Physiol. стр. 574-591 (148) 1959 г.
- ^ Д.Х. Хьюбель и Т.Н. Визель Рецептивные поля, бинокулярное взаимодействие и функциональная архитектура зрительной коры головного мозга кошки J. Physiol. 160 стр. 106–154 1962 г.
- ^ Мозг и визуальное восприятие: история 25-летнего сотрудничества Д. Х. Хьюбель и Т. Н. Визель, Оксфорд, 2005 г.