Эволюционный алгоритм
| Часть серии о |
| Искусственный интеллект |
|---|
В вычислительном интеллекте (CI) эволюционный алгоритм ( EA ) является подмножеством эволюционных вычислений , [1] общий метаэвристической оптимизации алгоритм на основе совокупности . ЭА использует механизмы, вдохновленные биологической эволюцией , такие как размножение , мутация , рекомбинация и отбор . Кандидаты на решение задачи оптимизации играют роль особей в популяции, а функция приспособленности определяет качество решений (см. также функцию потерь ). Эволюция популяции тогда происходит после многократного применения вышеуказанных операторов.
Эволюционные алгоритмы часто хорошо аппроксимируют решения всех типов задач, поскольку в идеале они не делают никаких предположений относительно лежащего в их основе ландшафта пригодности . Методы эволюционных алгоритмов, применяемые для моделирования биологической эволюции, обычно ограничиваются исследованием микроэволюционных процессов и моделями планирования, основанными на клеточных процессах. В большинстве реальных применений советников сложность вычислений является сдерживающим фактором. [2] Фактически, эта вычислительная сложность связана с оценкой функции приспособленности. Фитнес-аппроксимация является одним из решений преодоления этой трудности. Однако, казалось бы, простой советник может решить зачастую сложные проблемы; [3] [4] [5] следовательно, прямой связи между сложностью алгоритма и сложностью задачи может не быть.
Выполнение
[ редактировать ]Ниже приведен пример общего одноцелевого генетического алгоритма .
сгенерируйте начальную популяцию особей Шаг первый: Случайным образом . (Первое поколение)
Шаг второй: Повторите следующие шаги регенерации до завершения:
- Оценить приспособленность каждого индивидуума в популяции (ограничение по времени, достигнутая достаточная приспособленность и т. д.)
- Отберите наиболее приспособленных особей для размножения . (Родители)
- Выводите новых особей посредством операций скрещивания и мутации , чтобы дать потомство .
- Заменить наименее приспособленных особей популяции новыми особями.
Типы
[ редактировать ]Подобные методы различаются генетическим представлением и другими деталями реализации, а также характером конкретной прикладной задачи.
- Генетический алгоритм – это самый популярный тип советников. Решение проблемы ищут в виде цепочек чисел (традиционно двоичных, хотя лучшими представлениями обычно являются те, которые что-то отражают решаемую проблему), [2] применяя такие операторы, как рекомбинация и мутация (иногда один, иногда оба). Этот тип советника часто используется в задачах оптимизации .
- Генетическое программирование . Здесь решения представлены в виде компьютерных программ, и их пригодность определяется их способностью решать вычислительную задачу. Существует множество вариантов генетического программирования, включая декартово генетическое программирование , программирование экспрессии генов , грамматическую эволюцию , линейное генетическое программирование , программирование мультивыражений и т. д.
- Эволюционное программирование . Подобно генетическому программированию, но структура программы фиксирована, а ее числовые параметры могут изменяться.
- Стратегия эволюции . Работает с векторами действительных чисел как представлениями решений и обычно использует самоадаптирующуюся скорость мутаций. Метод в основном используется для численной оптимизации, хотя существуют варианты и для комбинаторных задач. [6] [7]
- Дифференциальная эволюция – основана на векторных разностях и поэтому в первую очередь подходит для задач численной оптимизации .
- Коэволюционный алгоритм . Похож на генетические алгоритмы и стратегии эволюции, но созданные решения сравниваются на основе их результатов взаимодействия с другими решениями. Решения могут либо конкурировать, либо сотрудничать в процессе поиска. Коэволюционные алгоритмы часто используются в сценариях, где фитнес-среда динамична, сложна или предполагает конкурентное взаимодействие. [8] [9]
- Нейроэволюция . Аналогично генетическому программированию, но геномы представляют собой искусственные нейронные сети, описывая структуру и вес связей. Кодирование генома может быть прямым или косвенным.
- Система обучающих классификаторов . Здесь решением является набор классификаторов (правил или условий). Мичиган-LCS развивается на уровне отдельных классификаторов, тогда как Питтсбург-LCS использует совокупности наборов классификаторов. Первоначально классификаторы были только двоичными, но теперь включают в себя реальные типы, типы нейронной сети или S-выражения . Фитнесс обычно определяется либо с помощью обучения с подкреплением, основанного на силе или точности, либо с помощью подхода обучения с учителем .
- Алгоритмы качества и разнообразия . Алгоритмы QD одновременно нацелены на получение высококачественных и разнообразных решений. В отличие от традиционных алгоритмов оптимизации, которые сосредоточены исключительно на поиске наилучшего решения проблемы, алгоритмы QD исследуют широкий спектр решений в проблемном пространстве и сохраняют те из них, которые не только высокоэффективны, но также разнообразны и уникальны. [10] [11] [12]
Теоретическая основа
[ редактировать ]Следующие теоретические принципы применимы ко всем или почти ко всем советникам.
Теорема «Нет бесплатного обеда»
[ редактировать ]Теорема оптимизации об отсутствии бесплатного обеда утверждает, что все стратегии оптимизации одинаково эффективны, когда рассматривается набор всех оптимизационных задач. При тех же условиях ни один эволюционный алгоритм не является фундаментально лучше другого. Это возможно только в том случае, если набор всех задач ограничен. Именно это неизбежно и происходит на практике. Следовательно, чтобы улучшить EA, он должен использовать знания о проблеме в той или иной форме (например, путем выбора определенной силы мутации или кодирования, адаптированного к проблеме ). Таким образом, если сравниваются два советника, это ограничение подразумевается. Кроме того, эксперт может использовать знания, специфичные для конкретной проблемы, например, не создавая случайным образом всю стартовую популяцию, а создавая некоторых индивидуумов с помощью эвристики или других процедур. [13] [14] Другая возможность адаптировать советник к заданной проблемной области — задействовать подходящие эвристики, процедуры локального поиска или другие процедуры, связанные с проблемой, в процессе генерации потомка. Эта форма расширения советника также известна как меметический алгоритм . Оба расширения играют важную роль в практических приложениях, поскольку могут ускорить процесс поиска и сделать его более надежным. [13] [15]
Конвергенция
[ редактировать ]Для ЭА, в которых для формирования последующего поколения, помимо потомства, используется как минимум лучшая особь родительского поколения (так называемые элитарные ЭА), существует общее доказательство сходимости при условии существования оптимума . Без ограничения общности для доказательства предполагается максимальный перебор:
Из свойства элитарного принятия потомства и существования оптимума следует, что в каждом поколении улучшение физической формы соответствующего лучшего человека произойдет с вероятностью . Таким образом:
Т.е. значения приспособленности представляют собой монотонно неубывающую последовательность , которая ограничена в силу существования оптимума. Отсюда следует сходимость последовательности к оптимуму.
Поскольку в доказательстве не говорится о скорости сходимости, оно мало поможет в практическом применении советников. Но это оправдывает рекомендацию использовать элитарные советники. Однако при использовании обычной модели панмиктической популяции элитарные ЭА склонны к преждевременной сходимости в большей степени, чем неэлитарные. [16] В модели панмиктической популяции выбор партнера (шаг 2 раздела, посвященного реализации) таков, что каждый человек во всей популяции имеет право стать партнером. В непанмиктических популяциях отбор соответствующим образом ограничен, так что скорость расселения лучших особей снижается по сравнению с панмиктическими. Таким образом, общий риск преждевременной конвергенции элитарных ЭА может быть значительно снижен с помощью подходящих популяционных моделей, ограничивающих выбор партнера. [17] [18]
Виртуальные алфавиты
[ редактировать ]С помощью теории виртуальных алфавитов Дэвид Э. Голдберг показал в 1990 году, что, используя представление с действительными числами, советник, который использует классические операторы рекомбинации (например, равномерный или n-точечный кроссовер), не может достичь определенных областей пространства поиска, в отличие от кодированию двоичными числами. [19] Это приводит к рекомендации для советников с реальным представлением использовать арифметические операторы для рекомбинации (например, среднее арифметическое или промежуточную рекомбинацию). При наличии подходящих операторов вещественные представления более эффективны, чем двоичные, вопреки ранее существовавшему мнению. [20] [21]
Сравнение с биологическими процессами
[ редактировать ]Возможное ограничение [ по мнению кого? ] Причиной многих эволюционных алгоритмов является отсутствие в них четкого различия между генотипом и фенотипом . В природе оплодотворенная яйцеклетка претерпевает сложный процесс, известный как эмбриогенез , чтобы стать зрелым фенотипом . Считается, что такое косвенное кодирование делает генетический поиск более надежным (т.е. снижает вероятность фатальных мутаций), а также может улучшить к эволюции . способность организма [22] [23] Такое косвенное (также известное как генеративное или развивающее) кодирование также позволяет эволюции использовать закономерности окружающей среды. [24] Недавние работы в области искусственной эмбриогенеза или систем искусственного развития направлены на решение этих проблем. А программирование экспрессии генов успешно исследует систему генотип-фенотип, где генотип состоит из линейных мультигенных хромосом фиксированной длины, а фенотип состоит из множества деревьев экспрессии или компьютерных программ разных размеров и форм. [25] [ неправильный синтез? ]
Сравнение с методами Монте-Карло
[ редактировать ]Оба класса методов общими являются то, что их отдельные шаги поиска определяются случайно. Однако главное отличие состоит в том, что эксперты, как и многие другие метаэвристики, учатся на прошлых шагах поиска и включают этот опыт в выполнение следующих шагов поиска в форме, специфичной для метода. В случае с ЭА это осуществляется в первую очередь через операторов отбора по фитнесу для выбора партнера и формирования следующего поколения. А во-вторых, по типу шагов поиска: в ЭА они начинают с текущего решения и меняют его или смешивают информацию двух решений. Напротив, при поиске новых решений с помощью методов Монте-Карло обычно нет связи с существующими решениями.
С другой стороны, если пространство поиска задачи таково, что изучать нечего, методы Монте-Карло являются подходящим инструментом, поскольку они не содержат каких-либо алгоритмических накладных расходов, которые пытаются сделать соответствующие выводы из предыдущего поиска. Примером таких задач является пресловутый поиск иголки в стоге сена , например, в виде плоской (гипер)плоскости с единственной узкой вершиной.
Приложения
[ редактировать ]Области практического применения эволюционных алгоритмов практически безграничны. [5] и варьируются от промышленности, [26] [27] инженерия, [2] [3] [28] сложный график, [4] [29] [30] сельское хозяйство, [31] планирование движения робота [32] и финансы [33] [34] исследовать [35] [36] и искусство . Применение эволюционного алгоритма требует некоторого переосмысления со стороны неопытного пользователя, поскольку подход к задаче с использованием ЭА отличается от традиционных точных методов и обычно не входит в учебную программу инженеров или других дисциплин. Например, расчет пригодности должен не только сформулировать цель, но и поддерживать процесс эволюционного поиска ее достижения, например, путем поощрения улучшений, которые еще не приводят к лучшей оценке исходных критериев качества. Например, если в задаче планирования необходимо избежать пикового использования ресурсов, таких как размещение персонала или потребление энергии, недостаточно оценить максимальное использование. Скорее, следует также фиксировать количество и продолжительность превышений все еще приемлемого уровня, чтобы вознаграждать за снижение уровня ниже фактического максимального пикового значения. [37] Поэтому существуют некоторые публикации, ориентированные на новичков и призванные помочь им избежать ошибок, а также привести прикладной проект к успеху. [37] [38] [39] Сюда входит прояснение фундаментального вопроса о том, когда следует использовать советник для решения проблемы, а когда лучше этого не делать.
Связанные методы
[ редактировать ]Роевые алгоритмы [ нужны разъяснения ] включать:
- Оптимизация колонии муравьев основана на идеях добывания пищи с помощью феромонов для формирования путей. [40] В первую очередь подходит для комбинаторной оптимизации и на графах . задач
- Алгоритм побега-корня (RRA) основан на функции побегов и корней растений в природе. [41]
- Алгоритм искусственной пчелиной семьи основан на поведении пчел при кормлении. В первую очередь предложен для численной оптимизации и расширен для решения комбинаторных, ограниченных и многокритериальных задач оптимизации.
- Алгоритм пчел основан на кормовом поведении медоносных пчел. Он применяется во многих приложениях, таких как маршрутизация и планирование.
- Поиск кукушки вдохновлен насиживающим паразитизмом кукушек . Он также использует полеты Леви и поэтому подходит для глобальной оптимизации . задач
- Оптимизация роя частиц основана на идеях стайного поведения животных. [40] Также в первую очередь подходит для задач численной оптимизации .
Другие метаэвристические методы, основанные на популяциях
[ редактировать ]- Охотничий поиск – метод, вдохновленный групповой охотой на некоторых животных, например волков, которые организуют свое положение, чтобы окружить добычу, каждого из них относительно положения других и особенно положения их лидера. Это метод непрерывной оптимизации. [42] адаптирован как метод комбинаторной оптимизации. [43]
- Адаптивный многомерный поиск . В отличие от метаэвристических методов, вдохновленных природой, алгоритм адаптивного многомерного поиска не реализует какую-либо метафору в качестве основного принципа. Скорее, он использует простой метод, ориентированный на производительность, основанный на обновлении параметра коэффициента размерности поиска (SDR) на каждой итерации. [44]
- Алгоритм Firefly основан на поведении светлячков, привлекающих друг друга мигающим светом. Это особенно полезно для мультимодальной оптимизации.
- Поиск гармонии - основан на представлениях о поведении музыкантов в поисках лучших гармоний. Этот алгоритм подходит для комбинаторной оптимизации, а также оптимизации параметров.
- Гауссова адаптация – основана на теории информации. Используется для максимизации производительности производства, средней пригодности или средней информации . См., например, Энтропию в термодинамике и теории информации .
- Меметический алгоритм – гибридный метод, вдохновленный понятием мема Ричарда Докинза . Он обычно принимает форму популяционного алгоритма в сочетании с индивидуальными процедурами обучения, способными выполнять локальные уточнения. Подчеркивает использование знаний по конкретным проблемам и пытается синергетически организовать локальный и глобальный поиск.
Примеры
[ редактировать ]В 2020 году Google заявила, что их AutoML-Zero может успешно заново открыть классические алгоритмы, такие как концепция нейронных сетей. [45]
Компьютерное моделирование Tierra и Avida пытается смоделировать макроэволюционную динамику.
Галерея
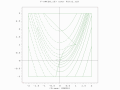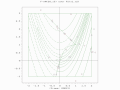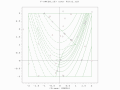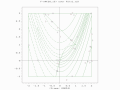
[ редактировать ]- Поиск советника с двумя популяциями по ограниченной функции Розенброка с ограниченным глобальным оптимумом
- Поиск советника с двумя популяциями по ограниченной функции Розенброка . Глобальный оптимум не ограничен.
- ЭА-поиск ограниченного оптимума функции Симионеску с двумя популяциями
Ссылки
[ редактировать ]- ^ Вихар, Пенсильвания (2016). «Эволюционные алгоритмы: критический обзор и его будущие перспективы». Международная конференция по глобальным тенденциям в области обработки сигналов, информационных вычислений и связи (ICGTSPICC) , 2016 г. Джалгаон. стр. 261–265. дои : 10.1109/ICGTSPICC.2016.7955308 . ISBN 978-1-5090-0467-6 . S2CID 22100336 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ Перейти обратно: а б с Кохун, Япония; Карро, Дж.; Линиг, Дж. (2003). «Эволюционные алгоритмы физического проектирования схем СБИС» в журнале «Достижения в области эволюционных вычислений: теория и приложения » (PDF) . Лондон: Springer Verlag. стр. 683–712. ISBN 978-3-540-43330-9 .
- ^ Перейти обратно: а б Словик, Адам; Квасьницкая, Галина (2020). «Эволюционные алгоритмы и их приложения к инженерным задачам» . Нейронные вычисления и их приложения . 32 (16): 12363–12379. дои : 10.1007/s00521-020-04832-8 . ISSN 0941-0643 . S2CID 212732659 .
- ^ Перейти обратно: а б Мика, Марек; Валигора, Гжегож; Венгларц, Ян (2011). «Моделирование и решение проблемы распределения сетевых ресурсов с использованием сетевых ресурсов для приложений рабочего процесса» . Журнал планирования . 14 (3): 291–306. дои : 10.1007/s10951-009-0158-0 . ISSN 1094-6136 . S2CID 31859338 .
- ^ Перейти обратно: а б «Международная конференция по применению эволюционных вычислений» . Конференция является частью серии Evo*. Материалы конференции публикуются издательством Springer . Проверено 23 декабря 2022 г.
- ^ Ниссен, Волкер; Краузе, Матиас (1994), «Ограниченная комбинаторная оптимизация со стратегией эволюции», в Ройше, Бернде (редактор), Fuzzy Logic , Informatik aktuell, Берлин, Гейдельберг: Springer, стр. 33–40, doi : 10.1007/978- 3-642-79386-8_5 , ISBN 978-3-642-79386-8
- ^ Коэльо, В.Н.; Коэльо, ИМ; Соуза, MJF; Оливейра, штат Техас; Кота, LP; Хаддад, Миннесота; Младенович, Н.; Сильва, RCP; Гимарайнш, ФГ (2016). «Гибридные самоадаптивные стратегии эволюции, управляемые структурами окрестности, для задач комбинаторной оптимизации». Эвол Компьютер . 24 (4): 637–666. дои : 10.1162/EVCO_a_00187 . ПМИД 27258842 . S2CID 13582781 .
- ^ Ма, Сяолян; Ли, Сяодун; Чжан, Цинфу; Тан, Кэ; Лян, Чжэнпин; Се, Вэйсинь; Чжу, Цзэсюань (2019), «Обзор кооперативных коэволюционных алгоритмов». , IEEE Transactions on Evolutionary Computation , 23 (3): 421–441, doi : 10.1109/TEVC.2018.2868770 , S2CID 125149900 , получено 22 мая 2023 г.
- ^ Попович, Елена; Буччи, Энтони; Виганд, Р. Пол; Де Йонг, Эдвин Д. (2012). «Коэволюционные принципы». В Розенберге, Гжегоже; Бек, Томас; Кок, Йост Н. (ред.). Справочник по естественным вычислениям . Берлин, Гейдельберг: Springer Berlin Heidelberg. стр. 987–1033. дои : 10.1007/978-3-540-92910-9_31 . ISBN 978-3-540-92910-9 .
- ^ Пью, Джастин К.; Сорос, Лиза Б.; Стэнли, Кеннет О. (12 июля 2016 г.). «Качественное разнообразие: новый рубеж эволюционных вычислений» . Границы робототехники и искусственного интеллекта . 3 . дои : 10.3389/frobt.2016.00040 . ISSN 2296-9144 .
- ^ Леман, Джоэл; Стэнли, Кеннет О. (12 июля 2011 г.). «Развитие разнообразия виртуальных существ посредством поиска новинок и местной конкуренции» . Материалы 13-й ежегодной конференции по генетическим и эволюционным вычислениям . Нью-Йорк, штат Нью-Йорк, США: ACM. стр. 211–218. дои : 10.1145/2001576.2001606 . ISBN 9781450305570 . S2CID 17338175 .
- ^ Калли, Антуан; Клюн, Джефф; Тарапор, Данеш; Муре, Жан-Батист (27 мая 2015 г.). «Роботы, которые могут адаптироваться, как животные» . Природа . 521 (7553): 503–507. arXiv : 1407.3501 . Бибкод : 2015Natur.521..503C . дои : 10.1038/nature14422 . ISSN 0028-0836 . ПМИД 26017452 . S2CID 3467239 .
- ^ Перейти обратно: а б Дэвис, Лоуренс (1991). Справочник по генетическим алгоритмам . Нью-Йорк: Ван Ностранд Рейнхольд. ISBN 0-442-00173-8 . ОСЛК 23081440 .
- ^ Линиг, Йенс; Брандт, Хольгер (1994), Давидор, Юваль; Швефель, Ханс-Пауль; Мэннер, Рейнхард (ред.), «Эволюционный алгоритм маршрутизации многочиповых модулей» , «Параллельное решение проблем из природы» — PPSN III , том. 866, Берлин, Гейдельберг: Springer, стр. 588–597, doi : 10.1007/3-540-58484-6_301 , ISBN. 978-3-540-58484-1 , получено 18 октября 2022 г.
- ^ Нери, Ферранте; Котта, Карлос; Москато, Пабло, ред. (2012). Справочник по меметическим алгоритмам . Исследования в области вычислительного интеллекта. Том. 379. Берлин, Гейдельберг: Springer Berlin Heidelberg. дои : 10.1007/978-3-642-23247-3 . ISBN 978-3-642-23246-6 .
- ^ Люнг, Йи; Гао, Юн; Сюй, Цзун-Бен (1997). «Степень разнообразия населения - взгляд на преждевременную конвергенцию генетических алгоритмов и анализ цепей Маркова» . Транзакции IEEE в нейронных сетях . 8 (5): 1165–1176. дои : 10.1109/72.623217 . ISSN 1045-9227 . ПМИД 18255718 .
- ^ Горж-Шлейтер, Мартина (1998), Эйбен, Агостон Э.; Назад, Томас; Шенауэр, Марк; Сульфур, Ханс-Пол (ред.), «Сравнительное исследование глобального и локального отбора в стратегиях эволюции» , Параллельное решение проблем из природы - PPSN V , Конспект лекций по информатике, том. 1498, Берлин, Гейдельберг: Springer Berlin Heidelberg, стр. 367–377, doi : 10.1007/bfb0056879 , ISBN 978-3-540-65078-2 , получено 21 октября 2022 г.
- ^ Дорронсоро, Бернабе; Альба, Энрике (2008). Клеточные генетические алгоритмы . Серия интерфейсов исследования операций/информатики. Том. 42. Бостон, Массачусетс: Springer США. дои : 10.1007/978-0-387-77610-1 . ISBN 978-0-387-77609-5 .
- ^ Гольдберг, Дэвид Э. (1990), Швефель, Ханс-Пол; Мэннер, Рейнхард (ред.), «Теория виртуальных алфавитов» , «Параллельное решение проблем из природы » , Конспект лекций по информатике, том. 496, Берлин/Гейдельберг: Springer-Verlag (опубликовано в 1991 г.), стр. 13–22, doi : 10.1007/bfb0029726 , ISBN 978-3-540-54148-6 , получено 22 октября 2022 г.
- ^ Стендер, Дж.; Хиллебранд, Э.; Кингдон, Дж. (1994). Генетические алгоритмы в оптимизации, симуляции и моделировании . Амстердам: IOS Press. ISBN 90-5199-180-0 . OCLC 47216370 .
- ^ Михалевич, Збигнев (1996). Генетические алгоритмы + структуры данных = программы эволюции (3-е изд.). Берлин Гейдельберг: Springer. ISBN 978-3-662-03315-9 . OCLC 851375253 .
- ^ Г.С. Хорнби и Дж.Б. Поллак. «Создание компонентов высокого уровня с генеративным представлением эволюции тела и мозга». Искусственная жизнь , 8(3):223–246, 2002.
- ^ Джефф Клюн, Бенджамин Бекманн, Чарльз Офриа и Роберт Пеннок. «Развитие скоординированной походки четвероногих с помощью генеративного кодирования HyperNEAT». Архивировано 3 июня 2016 г. в Wayback Machine . Труды Конгресса IEEE по эволюционным вычислениям, специальная секция по эволюционной робототехнике , 2009. Тронхейм, Норвегия.
- ^ Дж. Клюн, К. Офриа и Р. Т. Пеннок, «Как работает генеративное кодирование по мере уменьшения регулярности проблемы» , в PPSN (Г. Рудольф, Т. Янсен, С. М. Лукас, К. Полони и Н. Бьюме, ред. .), т. 5199 конспектов лекций по информатике , стр. 358–367, Springer, 2008.
- ^ Феррейра, К., 2001. «Программирование экспрессии генов: новый адаптивный алгоритм решения проблем» . Сложные системы , Том. 13, вып. 2: 87–129.
- ^ Санчес, Эрнесто; Скиллеро, Джованни; Тонда, Альберто (2012). Промышленное применение эволюционных алгоритмов . Справочная библиотека интеллектуальных систем. Том. 34. Берлин, Гейдельберг: Springer Berlin Heidelberg. дои : 10.1007/978-3-642-27467-1 . ISBN 978-3-642-27466-4 .
- ^ Миеттинен, Кайса (1999). Эволюционные алгоритмы в технике и информатике: последние достижения в области генетических алгоритмов, стратегий эволюции, эволюционного программирования, генетического программирования и промышленных приложений . Чичестер: Уайли и сыновья. ISBN 0-585-29445-3 . OCLC 45728460 .
- ^ Ген, Мицуо; Ченг, Жуньвэй (17 декабря 1999 г.). Генетические алгоритмы и инженерная оптимизация . Серия Wiley по инженерному проектированию и автоматизации. Хобокен, Нью-Джерси, США: John Wiley & Sons, Inc. doi : 10.1002/9780470172261 . ISBN 978-0-470-17226-1 .
- ^ Дахал, Кешав П.; Тан, Кей Чен; Коулинг, Питер I. (2007). Эволюционное планирование . Берлин: Шпрингер. дои : 10.1007/978-3-540-48584-1 . ISBN 978-3-540-48584-1 . OCLC 184984689 .
- ^ Якоб, Вильфрид; Страк, Сильвия; Квинт, Александр; Бенгель, Гюнтер; Стаки, Карл-Уве; Зюсс, Вольфганг (22 апреля 2013 г.). «Быстрое перепланирование нескольких рабочих процессов для ограниченных гетерогенных ресурсов с использованием многокритериальных меметических вычислений» . Алгоритмы . 6 (2): 245–277. дои : 10.3390/a6020245 . ISSN 1999-4893 .
- ^ Майер, Дэвид Г. (2002). Эволюционные алгоритмы и сельскохозяйственные системы . Бостон, Массачусетс: Springer US. дои : 10.1007/978-1-4615-1717-7 . ISBN 978-1-4613-5693-6 .
- ^ Блюм, Кристиан (2000), Каньони, Стефано (редактор), «Оптимизированное создание операторов движения робота без столкновений с помощью эволюционного программного обеспечения GLEAM» , Реальные приложения эволюционных вычислений , LNCS 1803, vol. 1803, Берлин, Гейдельберг: Springer, стр. 330–341, doi : 10.1007/3-540-45561-2_32 , ISBN. 978-3-540-67353-8 , получено 28 декабря 2022 г.
- ^ Аранья, Клаус; Иба, Хитоши (2008), Вобке, Уэйн; Чжан, Мэнцзе (ред.), «Применение меметического алгоритма к задаче оптимизации портфеля» , AI 2008: Достижения в области искусственного интеллекта , Конспекты лекций по информатике, том. 5360, Берлин, Гейдельберг: Springer Berlin Heidelberg, стр. 512–521, doi : 10.1007/978-3-540-89378-3_52 , ISBN 978-3-540-89377-6 , получено 23 декабря 2022 г.
- ^ Чен, Шу-Хэн, изд. (2002). Эволюционные вычисления в экономике и финансах . Исследования нечеткости и мягких вычислений. Том. 100. Гейдельберг: Physica-Verlag HD. дои : 10.1007/978-3-7908-1784-3 . ISBN 978-3-7908-2512-1 .
- ^ Лон, доктор юридических наук; Линден, Д.С.; Хорнби, Г.С.; Краус, ВФ (июнь 2004 г.). «Эволюционная конструкция антенны X-диапазона для миссии НАСА Space Technology 5» . Симпозиум Общества антенн и распространения IEEE, 2004 г. Том. 3. С. 2313–2316 Том 3. дои : 10.1109/APS.2004.1331834 . hdl : 2060/20030067398 . ISBN 0-7803-8302-8 .
- ^ Фогель, Гэри; Корн, Дэвид (2003). Эволюционные вычисления в биоинформатике . Эльзевир. дои : 10.1016/b978-1-55860-797-2.x5000-8 . ISBN 978-1-55860-797-2 .
- ^ Перейти обратно: а б Якоб, Уилфрид (2021), Успешное применение эволюционных алгоритмов - руководство, полученное на основе реальных приложений , KIT Scientific Work Papers, vol. 170, Карлсруэ, ФРГ: KIT Scientific Publishing, arXiv : 2107.11300 , doi : 10.5445/IR/1000135763 , S2CID 236318422 , получено 23 декабря 2022 г.
- ^ Уитли, Даррелл (2001). «Обзор эволюционных алгоритмов: практические вопросы и распространенные подводные камни» . Информационные и программные технологии . 43 (14): 817–831. дои : 10.1016/S0950-5849(01)00188-4 . S2CID 18637958 .
- ^ Эйбен, А.Е.; Смит, Дж. Э. (2015). «Работа с эволюционными алгоритмами». Введение в эволюционные вычисления . Серия Natural Computing (2-е изд.). Берлин, Гейдельберг: Springer Berlin Heidelberg. стр. 147–163. дои : 10.1007/978-3-662-44874-8 . ISBN 978-3-662-44873-1 . S2CID 20912932 .
- ^ Перейти обратно: а б Словик, Адам; Квасьницкая, Галина (2018). «Природные методы и их отраслевое применение — алгоритмы роевого интеллекта». Транзакции IEEE по промышленной информатике . 14 (3). Институт инженеров по электротехнике и электронике (IEEE): 1004–1015. дои : 10.1109/tii.2017.2786782 . ISSN 1551-3203 . S2CID 3707290 .
- ^ Ф. Меррих-Баят, «Алгоритм корня побега: метаэвристика для решения задач унимодальной и мультимодальной оптимизации, вдохновленная побегами и корнями растений в природе», Applied Soft Computing , Vol. 33, стр. 292–303, 2015 г.
- ^ Офтаде, Р.; Махджуб, MJ; Шариатпанахи, М. (октябрь 2010 г.). «Новый алгоритм метаэвристической оптимизации, вдохновленный групповой охотой на животных: охотничий поиск» . Компьютеры и математика с приложениями . 60 (7): 2087–2098. дои : 10.1016/j.camwa.2010.07.049 .
- ^ Амин Агаргор; Мохаммед Эссаид Риффи (2017). «Первая адаптация алгоритма охотничьего поиска для квадратичной задачи о назначениях». Достижения сотрудничества Европы и Ближнего Востока и Северной Африки в области информационных и коммуникационных технологий . Достижения в области интеллектуальных систем и вычислений. Том. 520. стр. 263–267. дои : 10.1007/978-3-319-46568-5_27 . ISBN 978-3-319-46567-8 .
- ^ Хасанчеби О., Каземзаде Азад С. (2015), «Адаптивный размерный поиск: новый метаэвристический алгоритм для оптимизации размеров дискретной фермы», Computers and Structures , 154, 1–16.
- ^ Гент, Эдд (13 апреля 2020 г.). «Искусственный интеллект развивается сам по себе» . Наука | АААС . Архивировано из оригинала 16 апреля 2020 года . Проверено 16 апреля 2020 г.
- ^ Симионеску, Пенсильвания; Дозье, Г.В.; Уэйнрайт, Р.Л. (2006). «Эволюционный алгоритм с двумя популяциями для задач оптимизации с ограничениями» . 2006 Международная конференция IEEE по эволюционным вычислениям . Ванкувер, Британская Колумбия, Канада: IEEE. стр. 1647–1653. дои : 10.1109/CEC.2006.1688506 . ISBN 978-0-7803-9487-2 . S2CID 1717817 .
- ^ Симионеску, Пенсильвания; Дозье, Г.В.; Уэйнрайт, Р.Л. (2006). «Эволюционный алгоритм с двумя популяциями для задач оптимизации с ограничениями» (PDF) . 2006 Международная конференция IEEE по эволюционным вычислениям . Proc 2006 Международная конференция IEEE по эволюционным вычислениям. Ванкувер, Канада. стр. 1647–1653. дои : 10.1109/CEC.2006.1688506 . ISBN 0-7803-9487-9 . S2CID 1717817 . Проверено 7 января 2017 г.
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ Симионеску, Пенсильвания (2014). Инструменты компьютерного построения графиков и моделирования для пользователей AutoCAD (1-е изд.). Бока-Ратон, Флорида: CRC Press . ISBN 978-1-4822-5290-3 .
Внешние ссылки
[ редактировать ]Библиография
[ редактировать ]- Эшлок, Д. (2006), Эволюционные вычисления для моделирования и оптимизации , Спрингер, Нью-Йорк, doi:10.1007/0-387-31909-3 ISBN 0-387-22196-4 .
- Бек, Т. (1996), Эволюционные алгоритмы в теории и практике: стратегии эволюции, эволюционное программирование, генетические алгоритмы , Oxford Univ. Пресс, Нью-Йорк, ISBN 978-0-19-509971-3 .
- Бэк Т., Фогель Д., Михалевич З. (1999), Эволюционные вычисления 1: основные алгоритмы и операторы , CRC Press, Бока-Ратон, США, ISBN 978-0-7503-0664-5 .
- Бек Т., Фогель Д., Михалевич З. (2000), Эволюционные вычисления 2: продвинутые алгоритмы и операторы , CRC Press, Бока-Ратон, США, doi:10.1201/9781420034349 ISBN 978-0-3678-0637-8 .
- Банцхаф В., Нордин П., Келлер Р., Франконе Ф. (1998), Генетическое программирование – Введение , Морган Кауфманн, Сан-Франциско, ISBN 978-1-55860-510-7 .
- Эйбен А.Е., Смит Дж.Э. (2003), «Введение в эволюционные вычисления» , Springer, Гейдельберг, Нью-Йорк, doi:10.1007/978-3-662-44874-8. ISBN 978-3-662-44873-1 .
- Холланд, Дж. Х. (1992), Адаптация в естественных и искусственных системах , MIT Press, Кембридж, Массачусетс, ISBN 978-0-262-08213-6 .
- Михалевич З.; Фогель, Д.Б. (2004), Как решить проблему: современная эвристика . Шпрингер, Берлин, Гейдельберг, ISBN 978-3-642-06134-9 , номер номера: 10.1007/978-3-662-07807-5 .
- Бенко, Аттила; Доса, Дьёрдь; Туза, Жолт (2010). «Упаковка/покрытие контейнеров с доставкой, решено с развитием алгоритмов». 2010 Пятая международная конференция IEEE по биовычислениям: теории и приложения (BIC-TA) . стр. 298–302. дои : 10.1109/BICTA.2010.5645312 . ISBN 978-1-4244-6437-1 . S2CID 16875144 .
- Поли, Р.; Лэнгдон, ВБ; Макфи, Северная Каролина (2008). Полевое руководство по генетическому программированию . Lulu.com, бесплатно доступный в Интернете. ISBN 978-1-4092-0073-4 . Архивировано из оригинала 27 мая 2016 г. Проверено 5 марта 2011 г. [ самостоятельный источник ]
- Прайс К., Сторн Р.М., Лампинен Дж.А. (2005). Дифференциальная эволюция: практический подход к глобальной оптимизации , Шпрингер, Берлин, Гейдельберг, ISBN 978-3-642-42416-8 , номер номера: 10.1007/3-540-31306-0 .
- Ингорехнерберг (1971), Эволюционная стратегия - оптимизация технических систем согласно принципам биологической эволюции (кандидатская диссертация). Перепечатано Фромманом-Хольцбогом (1973). ISBN 3-7728-1642-8
- Ханс-Пауль Вёльфе (1974), Численная оптимизация компьютерных моделей (докторская диссертация). Перепечатано Биркхойзером (1977).
- Ханс-Поль Швефель (1995), Эволюция и поиск оптимума . Уайли и сыновья, Нью-Йорк. ISBN 0-471-57148-2
- Саймон, Д. (2013), Алгоритмы эволюционной оптимизации. Архивировано 10 марта 2014 г. в Wayback Machine , Wiley & Sons, ISBN 978-0-470-93741-9
- Крузе, Рудольф; Боргельт, Кристиан; Клавонн, Фрэнк; Мовес, Кристиан; Штайнбрехер, Матиас; Хелд, Паскаль (2013), Вычислительный интеллект: методологическое введение . Спрингер, Лондон. ISBN 978-1-4471-5012-1 , номер номера: 10.1007/978-1-4471-5013-8 .
- Рахман, Россхайри Абд.; Кендалл, Грэм; Рамли, Разамин; Джамари, Зайноддин; Ку-Махамуд, Ку Рухана (2017). «Состав корма для креветок с помощью эволюционного алгоритма с степенной эвристикой для преодоления ограничений» . Сложность . 2017 : 1–12. дои : 10.1155/2017/7053710 .