Алгоритм спиральной оптимизации

В математике алгоритм спиральной оптимизации (SPO) — это метаэвристика, вдохновленная спиральными явлениями в природе.

Первый алгоритм SPO был предложен для двумерной безусловной оптимизации. ^[1] на основе двумерных спиральных моделей. Это было распространено на n-мерные проблемы путем обобщения двумерной спиральной модели до n-мерной спиральной модели. ^[2] Имеются эффективные настройки алгоритма SPO: настройка направления периодического спуска. ^[3] и настройки сходимости. ^[4]

Метафора [ править ]

Мотивацией для сосредоточения внимания на спиральных явлениях было понимание того, что динамика, порождающая логарифмические спирали, разделяет поведение диверсификации и интенсификации. Поведение диверсификации может способствовать глобальному поиску (исследование), а поведение интенсификации обеспечивает интенсивный поиск вокруг текущего найденного хорошего решения (эксплуатация).

Алгоритм [ править ]

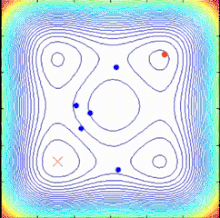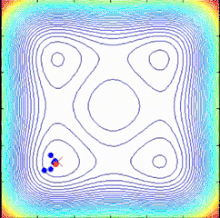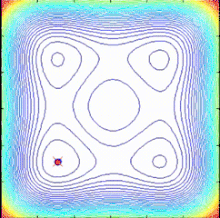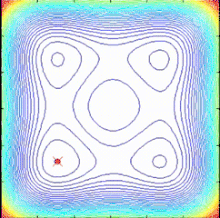
Алгоритм SPO — это алгоритм многоточечного поиска , не имеющий градиента целевой функции , который использует несколько спиральных моделей, которые можно описать как детерминированные динамические системы. Поскольку точки поиска следуют логарифмическому принципу Если спиральные траектории направлены к общему центру, определенному как текущая лучшая точка, можно найти лучшие решения и обновить общий центр.

Общий алгоритм SPO для задачи минимизации на максимальной итерации $k_{\max }$ (критерий завершения) следующий:

0) Set the number of search points  $m\geq 2$  and the maximum iteration number  $k_{\max }$ .
1) Place the initial search points  $x_{i}(0)\in \mathbb {R} ^{n}~(i=1,\ldots ,m)$  and determine the center  $x^{\star }(0)=x_{i_{\text{b}}}(0)$ ,  $\displaystyle i_{\text{b}}=\mathop {\text{argmin}} _{i=1,\ldots ,m}\{f(x_{i}(0))\}$ ,and then set  $k=0$ .
2) Decide the step rate  $r(k)$  by a rule.
3) Update the search points:  $x_{i}(k+1)=x^{\star }(k)+r(k)R(\theta )(x_{i}(k)-x^{\star }(k))\quad (i=1,\ldots ,m).$ 
4) Update the center:  $x^{\star }(k+1)={\begin{cases}x_{i_{\text{b}}}(k+1)&{\big (}{\text{if }}f(x_{i_{\text{b}}}(k+1))<f(x^{\star }(k)){\big )},\\x^{\star }(k)&{\big (}{\text{otherwise}}{\big )},\end{cases}}$  where  $\displaystyle i_{\text{b}}=\mathop {\text{argmin}} _{i=1,\ldots ,m}\{f(x_{i}(k+1))\}$ .
5) Set  $k:=k+1$ . If  $k=k_{\max }$  is satisfied then terminate and output  $x^{\star }(k)$ . Otherwise, return to Step 2).

Настройка [ править ]

Производительность поиска зависит от настройки составной матрицы вращения. $R(\theta )$ , скорость шага $r(k)$ , а начальные точки $x_{i}(0)~(i=1,\ldots ,m)$ . Следующие настройки являются новыми и эффективными.

Настройка 1 (Настройка направления периодического снижения) [ править ]

Этот параметр является эффективным параметром для задач большой размерности при максимальной итерации. $k_{\max }$ . Условия на $R(\theta )$ и $x_{i}(0)~(i=1,\ldots ,m)$ вместе гарантируют, что спиральные модели периодически генерируют направления спуска. Состояние $r(k)$ работает над использованием периодических направлений спуска при прекращении поиска $k_{\max }$ .

Набор $R(\theta )$ следующее: $R(\theta )={\begin{bmatrix}0_{n-1}^{\top }&-1\\I_{n-1}&0_{n-1}\\\end{bmatrix}}$ где $I_{n-1}$ это $(n-1)\times (n-1)$ идентификационная матрица и $0_{n-1}$ это $(n-1)\times 1$ нулевой вектор.
Разместите начальные точки $x_{i}(0)\in \mathbb {R} ^{n}$ $(i=1,\ldots ,m)$ случайным образом, чтобы удовлетворить следующему условию:

$\min _{i=1,\ldots ,m}\{\max _{j=1,\ldots ,m}{\bigl \{}{\text{rank}}{\bigl [}d_{j,i}(0)~R(\theta )d_{j,i}(0)~~\cdots ~~R(\theta )^{2n-1}d_{j,i}(0){\bigr ]}{\bigr \}}{\bigr \}}=n$ где $d_{j,i}(0)=x_{j}(0)-x_{i}(0)$ . Обратите внимание, что это условие почти полностью удовлетворяется при случайном размещении, поэтому никакая проверка на самом деле недопустима.

Набор $r(k)$ на шаге 2) следующим образом: $r(k)=r={\sqrt[{k_{\max }}]{\delta }}~~~~{\text{(constant value)}}$ где достаточно малый $\delta >0$ такой как $\delta =1/k_{\max }$ или $\delta =10^{-3}$ . ^[3]

Настройка 2 (Настройка конвергенции) [ редактировать ]

Эта настройка гарантирует, что алгоритм SPO сходится к стационарной точке при максимальной итерации. $k_{\max }=\infty$ . Настройки $R(\theta )$ и начальные точки $x_{i}(0)~(i=1,\ldots ,m)$ аналогичны приведенной выше настройке 1. Настройка $r(k)$ заключается в следующем.

Набор $r(k)$ на шаге 2) следующим образом: $r(k)={\begin{cases}1&(k^{\star }\leqq k\leqq k^{\star }+2n-1),\\h&(k\geqq k^{\star }+2n),\end{cases}}$ где $k^{\star }$ это итерация , когда центр заново обновляется на шаге 4) и $h={\sqrt[{2n}]{\delta }},\delta \in (0,1)$ такой как $\delta =0.5$ . Таким образом, мы должны добавить следующие правила о $k^{\star }$ к алгоритму:

•(Шаг 1)

k^{\star }=0

.

•(Шаг 4) Если

x^{\star }(k+1)\neq x^{\star }(k)

затем

k^{\star }=k+1

. ^[4]

Будущие работы

Алгоритмы с указанными выше настройками являются детерминированными . Таким образом, включение некоторых случайных операций делает этот алгоритм мощным средством глобальной оптимизации . Круз-Дуарте и др. ^[5] продемонстрировал это, включив стохастические возмущения в спиральные поисковые траектории. Однако эта дверь остается открытой для дальнейших исследований.
Найти подходящий баланс между спиралями диверсификации и интенсификации в зависимости от целевого класса проблем (включая $k_{\max }$ ) важно для повышения производительности.

Расширенные работы [ править ]

По SPO было проведено множество расширенных исследований из-за его простой структуры и концепции; эти исследования помогли улучшить эффективность глобального поиска и предложили новые приложения. ^[6]^[7]^[8]^[9]^[10]^[11]

Ссылки [ править ]

^ Тамура, К.; Ясуда, К. (2011). «Первичное исследование оптимизации, вдохновленной спиральной динамикой». Сделки IEEJ по электротехнике и электронике . 6 (С1): 98–100. дои : 10.1002/tee.20628 . S2CID 109093423 .
^ Тамура, К.; Ясуда, К. (2011). «Оптимизация, вдохновленная спиральной динамикой» . Журнал передового вычислительного интеллекта и интеллектуальной информатики . 132 (5): 1116–1121. дои : 10.20965/jaciii.2011.p1116 .
^ Jump up to: Перейти обратно: ^а ^б Тамура, К.; Ясуда, К. (2016). «Алгоритм спиральной оптимизации с использованием периодических направлений спуска» . Журнал SICE по контролю, измерениям и системной интеграции . 6 (3): 133–143. Бибкод : 2016JCMSI...9..134T . дои : 10.9746/jcmsi.9.134 .
^ Jump up to: Перейти обратно: ^а ^б Тамура, К.; Ясуда, К. (2020). «Алгоритм спиральной оптимизации: условия и настройки сходимости». Транзакции IEEE по системам, человеку и кибернетике: системы . 50 (1): 360–375. дои : 10.1109/TSMC.2017.2695577 . S2CID 126109444 .
^ Круз-Дуарте, Хорхе М.; Мартин-Диас, Игнасио; Муньос-Минхарес, Ю.; Санчес-Галиндо, Луис А.; Авина-Сервантес, Хуан Г.; Гарсиа-Перес, Артуро; Корреа-Сели, К. Родриго (2017). «Первичное исследование алгоритма стохастической спиральной оптимизации» . Международная осенняя встреча IEEE по энергетике, электронике и вычислениям (ROPEC) 2017 г. стр. 1–6. дои : 10.1109/ROPEC.2017.8261609 . ISBN 978-1-5386-0819-7 . S2CID 37580653 .
^ Насир, АНК; Тохи, МО (2015). «Улучшенный алгоритм спиральной динамической оптимизации с инженерным применением». Транзакции IEEE по системам, человеку и кибернетике: системы . 45 (6): 943–954. дои : 10.1109/tsmc.2014.2383995 . S2CID 24253496 .
^ Насир, АНК; Исмаил, РМТР; Тохи, МО (2016). «Метаэвристический алгоритм адаптивной спиральной динамики для глобальной оптимизации с применением к моделированию гибкой системы» (PDF) . Прикладное математическое моделирование . 40 (9–10): 5442–5461. дои : 10.1016/j.apm.2016.01.002 .
^ Уади, А.; Бентарзи, Х.; Ресиуи, А. (2013). «Многокритериальное проектирование цифровых фильтров с использованием метода спиральной оптимизации» . СпрингерПлюс . 2 (461): 697–707. дои : 10.1186/2193-1801-2-461 . ПМЦ 3786071 . ПМИД 24083108 .
^ Бенасла, Л.; Бельмадани, А.; Рахли, М. (2014). «Алгоритм спиральной оптимизации для решения комбинированных экономических задач и диспетчеризации выбросов». Международный журнал электроэнергетики и энергетических систем . 62 : 163–174. Бибкод : 2014IJEPE..62..163B . дои : 10.1016/j.ijepes.2014.04.037 .
^ Сидарто, Калифорния; Кания, А. (2015). «Нахождение всех решений систем нелинейных уравнений с использованием спиральной динамики вдохновило на оптимизацию с помощью кластеризации» . Журнал передового вычислительного интеллекта и интеллектуальной информатики . 19 (5): 697–707. дои : 10.20965/jaciii.2015.p0697 .
^ Каве, А.; Маджуби, С. (октябрь 2019 г.). «Подход к оптимизации спирали гипотрохоиды для оптимизации размеров и компоновки ферменных конструкций с множеством ограничений по частоте». Инженерное дело с компьютерами . 35 (4): 1443–1462. дои : 10.1007/s00366-018-0675-6 . S2CID 54457145 .

[tamura11a-1] Тамура, К.; Ясуда, К. (2011). «Первичное исследование оптимизации, вдохновленной спиральной динамикой». Сделки IEEJ по электротехнике и электронике . 6 (С1): 98–100. дои : 10.1002/tee.20628 . S2CID 109093423 .

[tamura11b-2] Тамура, К.; Ясуда, К. (2011). «Оптимизация, вдохновленная спиральной динамикой» . Журнал передового вычислительного интеллекта и интеллектуальной информатики . 132 (5): 1116–1121. дои : 10.20965/jaciii.2011.p1116 .

[tamura16a-3] Jump up to: Перейти обратно: ^а ^б Тамура, К.; Ясуда, К. (2016). «Алгоритм спиральной оптимизации с использованием периодических направлений спуска» . Журнал SICE по контролю, измерениям и системной интеграции . 6 (3): 133–143. Бибкод : 2016JCMSI...9..134T . дои : 10.9746/jcmsi.9.134 .

[tamura17a-4] Jump up to: Перейти обратно: ^а ^б Тамура, К.; Ясуда, К. (2020). «Алгоритм спиральной оптимизации: условия и настройки сходимости». Транзакции IEEE по системам, человеку и кибернетике: системы . 50 (1): 360–375. дои : 10.1109/TSMC.2017.2695577 . S2CID 126109444 .

[5] Круз-Дуарте, Хорхе М.; Мартин-Диас, Игнасио; Муньос-Минхарес, Ю.; Санчес-Галиндо, Луис А.; Авина-Сервантес, Хуан Г.; Гарсиа-Перес, Артуро; Корреа-Сели, К. Родриго (2017). «Первичное исследование алгоритма стохастической спиральной оптимизации» . Международная осенняя встреча IEEE по энергетике, электронике и вычислениям (ROPEC) 2017 г. стр. 1–6. дои : 10.1109/ROPEC.2017.8261609 . ISBN 978-1-5386-0819-7 . S2CID 37580653 .

[nasir15a-6] Насир, АНК; Тохи, МО (2015). «Улучшенный алгоритм спиральной динамической оптимизации с инженерным применением». Транзакции IEEE по системам, человеку и кибернетике: системы . 45 (6): 943–954. дои : 10.1109/tsmc.2014.2383995 . S2CID 24253496 .

[nasir16a-7] Насир, АНК; Исмаил, РМТР; Тохи, МО (2016). «Метаэвристический алгоритм адаптивной спиральной динамики для глобальной оптимизации с применением к моделированию гибкой системы» (PDF) . Прикладное математическое моделирование . 40 (9–10): 5442–5461. дои : 10.1016/j.apm.2016.01.002 .

[ouadi13a-8] Уади, А.; Бентарзи, Х.; Ресиуи, А. (2013). «Многокритериальное проектирование цифровых фильтров с использованием метода спиральной оптимизации» . СпрингерПлюс . 2 (461): 697–707. дои : 10.1186/2193-1801-2-461 . ПМЦ 3786071 . ПМИД 24083108 .

[benasla14a-9] Бенасла, Л.; Бельмадани, А.; Рахли, М. (2014). «Алгоритм спиральной оптимизации для решения комбинированных экономических задач и диспетчеризации выбросов». Международный журнал электроэнергетики и энергетических систем . 62 : 163–174. Бибкод : 2014IJEPE..62..163B . дои : 10.1016/j.ijepes.2014.04.037 .

[sidarto15a-10] Сидарто, Калифорния; Кания, А. (2015). «Нахождение всех решений систем нелинейных уравнений с использованием спиральной динамики вдохновило на оптимизацию с помощью кластеризации» . Журнал передового вычислительного интеллекта и интеллектуальной информатики . 19 (5): 697–707. дои : 10.20965/jaciii.2015.p0697 .

[KavehMahjoubi-11] Каве, А.; Маджуби, С. (октябрь 2019 г.). «Подход к оптимизации спирали гипотрохоиды для оптимизации размеров и компоновки ферменных конструкций с множеством ограничений по частоте». Инженерное дело с компьютерами . 35 (4): 1443–1462. дои : 10.1007/s00366-018-0675-6 . S2CID 54457145 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]