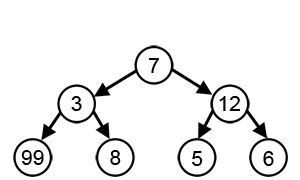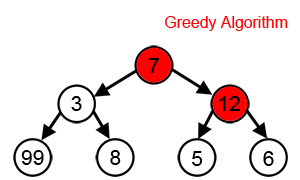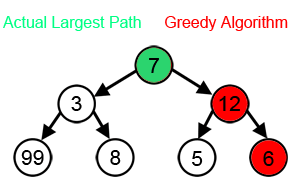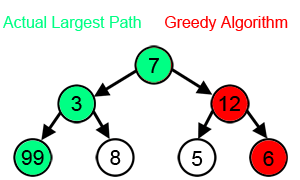
Жадный алгоритм

— Жадный алгоритм это любой алгоритм решения задач , который следует эвристике и делает локально оптимальный выбор на каждом этапе. ^[1] Во многих задачах жадная стратегия не дает оптимального решения, но жадная эвристика может дать локально оптимальные решения, которые приближаются к глобально оптимальному решению за разумный промежуток времени.

Например, жадная стратегия решения задачи коммивояжера (которая имеет высокую вычислительную сложность) представляет собой следующую эвристику: «На каждом этапе путешествия посещайте ближайший непосещенный город». Эта эвристика не направлена на поиск наилучшего решения, но завершается за разумное количество шагов; поиск оптимального решения такой сложной проблемы обычно требует неоправданно большого количества шагов. В математической оптимизации жадные алгоритмы оптимально решают комбинаторные задачи, обладающие свойствами матроидов , и дают аппроксимации с постоянным коэффициентом для задач оптимизации с субмодульной структурой.

Особенности [ править ]

Жадные алгоритмы дают хорошие решения некоторых математических задач , но не дают других. Большинство проблем, для решения которых они работают, будут иметь два свойства:

Жадный выбор недвижимости: Мы можем сделать любой выбор, который кажется лучшим в данный момент, а затем решить подзадачи, которые возникнут позже. Выбор, сделанный жадным алгоритмом, может зависеть от выбора, сделанного на данный момент, но не от будущего выбора или всех решений подзадачи. Он итеративно делает один жадный выбор за другим, сводя каждую данную проблему к меньшей. Другими словами, жадный алгоритм никогда не пересматривает свой выбор. В этом главное отличие от динамического программирования , которое является исчерпывающим и гарантированно находит решение. После каждого этапа динамическое программирование принимает решения на основе всех решений, принятых на предыдущем этапе, и может пересмотреть алгоритмический путь предыдущего этапа к решению.
Оптимальная подструктура: «Проблема имеет оптимальную подструктуру , если оптимальное решение проблемы содержит оптимальные решения подзадач». ^[2]

Случаи неудач [ править ]

Примеры того, как жадный алгоритм может не достичь оптимального решения.

Начиная с A, жадный алгоритм, который пытается найти максимум, следуя по наибольшему наклону, найдет локальный максимум в «m», не обращая внимания на глобальный максимум в «M».

Чтобы достичь наибольшей суммы, жадный алгоритм на каждом шаге будет выбирать то, что кажется оптимальным непосредственным выбором, поэтому на втором шаге он выберет 12 вместо 3 и не достигнет лучшего решения, которое содержит 99.

Жадные алгоритмы не могут дать оптимальное решение для многих других задач и могут даже дать единственное наихудшее из возможных решений. Одним из примеров является упомянутая выше задача коммивояжера : для каждого числа городов заданы расстояния между городами, для которых эвристика ближайшего соседа создает уникальный наихудший возможный тур. ^[3]Другие возможные примеры см. в разделе Эффект горизонта .

Типы [ править ]

Жадные алгоритмы можно охарактеризовать как «близорукие», а также как «невосстанавливаемые». Они идеальны только для задач, имеющих «оптимальную подструктуру». Несмотря на это, для многих простых задач лучше всего подходят жадные алгоритмы. Однако важно отметить, что жадный алгоритм можно использовать в качестве алгоритма выбора для определения приоритета вариантов в рамках поиска или алгоритма ветвей и границ. Есть несколько вариантов жадного алгоритма: ^[4]

Чисто жадные алгоритмы
Ортогональные жадные алгоритмы
Расслабленные жадные алгоритмы

Теория [ править ]

Жадные алгоритмы имеют долгую историю изучения в области комбинаторной оптимизации и теоретической информатики . Жадные эвристики, как известно, дают неоптимальные результаты при решении многих задач. ^[5] и поэтому естественные вопросы:

Для каких задач жадные алгоритмы работают оптимально?
Для каких задач жадные алгоритмы гарантируют приблизительно оптимальное решение?
Для каких задач жадный алгоритм гарантированно не даст оптимального решения?

Существует большой объем литературы, дающей ответы на эти вопросы как для общих классов задач, таких как матроиды , так и для конкретных задач, таких как покрытие множеств .

Матроиды [ править ]

Матроид — это математическая структура, которая обобщает понятие линейной независимости векторных пространств на произвольные множества. Если задача оптимизации имеет структуру матроида, то соответствующий жадный алгоритм решит ее оптимально. ^[6]

Субмодульные функции [ править ]

Функция $f$ определено на подмножествах множества $\Omega$ называется субмодулярным, если для любого $S,T\subseteq \Omega$ у нас есть это $f(S)+f(T)\geq f(S\cup T)+f(S\cap T)$ .

Предположим, кто-то хочет найти набор $S$ который максимизирует $f$ . Жадный алгоритм, создающий множество $S$ путем постепенного добавления элемента, который увеличивает $f$ наибольшее количество на каждом шаге, выдает на выходе набор, который по крайней мере $(1-1/e)\max _{X\subseteq \Omega }f(X)$ . ^[7] То есть жадность работает в пределах постоянного коэффициента $(1-1/e)\approx 0.63$ так же хорошо, как оптимальное решение.

Подобные гарантии доказуемы, когда дополнительные ограничения, такие как ограничения мощности, ^[8] накладываются на выходные данные, хотя часто требуются небольшие изменения в жадном алгоритме. Видеть ^[9] для обзора.

Другие проблемы с гарантиями [ править ]

Другие проблемы, для которых жадный алгоритм дает надежную гарантию, но не оптимальное решение, включают:

Многие из этих задач имеют совпадающие нижние границы; т. е. в худшем случае жадный алгоритм не будет работать лучше, чем гарантированный.

Приложения [ править ]

Жадные алгоритмы обычно (но не всегда) не могут найти глобально оптимальное решение, поскольку они обычно не обрабатывают все данные исчерпывающе. Они могут слишком рано принять на себя обязательства по определенному выбору, что не позволяет им найти лучшее общее решение позже. Например, все известные алгоритмы жадной раскраски для задачи раскраски графов и всех других NP-полных задач не всегда находят оптимальные решения. Тем не менее, они полезны, поскольку быстро придумывают и часто дают хорошее приближение к оптимуму.

Если можно доказать, что жадный алгоритм дает глобальный оптимум для данного класса задач, он обычно становится предпочтительным методом, поскольку он быстрее, чем другие методы оптимизации, такие как динамическое программирование . Примерами таких жадных алгоритмов являются алгоритм Краскала и алгоритм Прима для поиска минимальных остовных деревьев и алгоритм поиска оптимальных деревьев Хаффмана .

в сетевой маршрутизации Жадные алгоритмы появляются и . Используя жадную маршрутизацию, сообщение пересылается соседнему узлу, который «ближайший» к месту назначения. Понятие местоположения узла (и, следовательно, «близости») может определяться его физическим местоположением, как при географической маршрутизации , используемой в одноранговых сетях . Местоположение также может быть полностью искусственной конструкцией, как в маршрутизации маленького мира и распределенной хэш-таблице .

Примеры [ править ]

Для этого класса задач характерна задача выбора действий , цель которой состоит в том, чтобы выбрать максимальное количество действий, не конфликтующих друг с другом.
для Macintosh Цель компьютерной игры Crystal Quest — собирать кристаллы аналогично задаче коммивояжера . В игре есть демо-режим, в котором игра использует жадный алгоритм для доступа к каждому кристаллу. Искусственный интеллект не учитывает препятствия, поэтому демо-режим зачастую быстро заканчивается.
Поиск соответствия является примером жадного алгоритма, применяемого для аппроксимации сигнала.
Жадный алгоритм находит оптимальное решение проблемы Малфатти о поиске трех непересекающихся кругов внутри заданного треугольника, которые максимизируют общую площадь кругов; предполагается, что один и тот же жадный алгоритм оптимален для любого числа кругов.
Жадный алгоритм используется для построения дерева Хаффмана во время кодирования Хаффмана , где он находит оптимальное решение.
При обучении дерева решений обычно используются жадные алгоритмы, однако они не гарантируют нахождение оптимального решения.
- Одним из популярных таких алгоритмов является алгоритм ID3 для построения дерева решений.
Алгоритм Дейкстры и связанный с ним алгоритм поиска A* являются проверяемо оптимальными жадными алгоритмами для поиска графов и поиска кратчайшего пути .
- Поиск A* является условно оптимальным и требует « допустимой эвристики », которая не будет переоценивать стоимость пути.
Алгоритм Краскала и алгоритм Прима — жадные алгоритмы построения минимальных остовных деревьев заданного связного графа . Они всегда находят оптимальное решение, которое в целом может быть не единственным.
и Алгоритмы Sequitur Lempel -Ziv-Welch — это жадные алгоритмы индукции грамматики .

См. также [ править ]

Ссылки [ править ]

^ Блэк, Пол Э. (2 февраля 2005 г.). «жадный алгоритм» . Словарь алгоритмов и структур данных . Национальный институт стандартов и технологий США (NIST) . Проверено 17 августа 2012 г.
^ Кормен и др. 2001 , гл. 16.
^ Гутин, Григорий; Эй, Андерс; Зверович, Алексей (2002). «Коммивояжер не должен быть жадным: анализ доминирования эвристик жадного типа для TSP» . Дискретная прикладная математика . 117 (1–3): 81–86. дои : 10.1016/S0166-218X(01)00195-0 .
^ ДеВор, РА; Темляков В.Н. (12.1996). «Некоторые замечания о жадных алгоритмах» . Достижения в области вычислительной математики . 5 (1): 173–187. дои : 10.1007/BF02124742 . ISSN 1572-9044 .
^ Файги, 1998 г.
^ Пападимитриу и Стейглиц, 1998 г.
^ Немхаузер, Вулси и Фишер, 1978 г.
^ Бухбиндер и др. 2014 год
^ Краузе и Головин 2014.
^ «Лекция 5: Введение в алгоритмы аппроксимации» (PDF) . Расширенные алгоритмы (2IL45) — Конспекты курса . ТУ Эйндховена. Архивировано (PDF) из оригинала 9 октября 2022 г.

Источники [ править ]

Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2001). «16 жадных алгоритмов» . Введение в алгоритмы . МТИ Пресс. стр. 370–. ISBN 978-0-262-03293-3 .
Гутин, Григорий; Эй, Андерс; Зверович, Алексей (2002). «Коммивояжер не должен быть жадным: анализ доминирования эвристик жадного типа для TSP» . Дискретная прикладная математика . 117 (1–3): 81–86. дои : 10.1016/S0166-218X(01)00195-0 .
Банг-Йенсен, Йорген; Гутин, Григорий; Йо, Андерс (2004). «Когда жадный алгоритм дает сбой» . Дискретная оптимизация . 1 (2): 121–127. дои : 10.1016/j.disopt.2004.03.007 .
Бендалл, Гарет; Марго, Франсуа (2006). «Жадное сопротивление комбинаторных задач» . Дискретная оптимизация . 3 (4): 288–298. дои : 10.1016/j.disopt.2006.03.001 .
Файги, У. (1998). «Порог ln n для аппроксимации набора покрытия» (PDF) . Журнал АКМ . 45 (4): 634–652. дои : 10.1145/285055.285059 . S2CID 52827488 . Архивировано (PDF) из оригинала 9 октября 2022 г.
Немхаузер, Г.; Уолси, Луизиана; Фишер, М.Л. (1978). «Анализ приближений для максимизации субмодулярных функций множества — I» . Математическое программирование . 14 (1): 265–294. дои : 10.1007/BF01588971 . S2CID 206800425 .
Бухбиндер, Нив; Фельдман, Моран; Наор, Джозеф (Сеффи); Шварц, Рой (2014). «Субмодульная максимизация с ограничениями мощности» (PDF) . Материалы двадцать пятого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам . Общество промышленной и прикладной математики. дои : 10.1137/1.9781611973402.106 . ISBN 978-1-61197-340-2 . Архивировано (PDF) из оригинала 9 октября 2022 г.
Краузе, А.; Головин, Д. (2014). «Максимизация субмодульной функции» . В Бордо, Л.; Хамади, Ю.; Кохли, П. (ред.). Управляемость: практические подходы к сложным проблемам . Издательство Кембриджского университета. стр. 71–104. дои : 10.1017/CBO9781139177801.004 . ISBN 9781139177801 .
Пападимитриу, Христос Х .; Стейглиц, Кеннет (1998). Комбинаторная оптимизация: алгоритмы и сложность . Дувр.

Внешние ссылки [ править ]

«Жадный алгоритм» , Математическая энциклопедия , EMS Press , 2001 [1994]
Подарок, Ной. «Пример жадной монеты Python» .

[NISTg-1] Блэк, Пол Э. (2 февраля 2005 г.). «жадный алгоритм» . Словарь алгоритмов и структур данных . Национальный институт стандартов и технологий США (NIST) . Проверено 17 августа 2012 г.

[2] Кормен и др. 2001 , гл. 16.

[3] Гутин, Григорий; Эй, Андерс; Зверович, Алексей (2002). «Коммивояжер не должен быть жадным: анализ доминирования эвристик жадного типа для TSP» . Дискретная прикладная математика . 117 (1–3): 81–86. дои : 10.1016/S0166-218X(01)00195-0 .

[4] ДеВор, РА; Темляков В.Н. (12.1996). «Некоторые замечания о жадных алгоритмах» . Достижения в области вычислительной математики . 5 (1): 173–187. дои : 10.1007/BF02124742 . ISSN 1572-9044 .

[5] Файги, 1998 г.

[6] Пападимитриу и Стейглиц, 1998 г.

[7] Немхаузер, Вулси и Фишер, 1978 г.

[8] Бухбиндер и др. 2014 год

[9] Краузе и Головин 2014.

[10] «Лекция 5: Введение в алгоритмы аппроксимации» (PDF) . Расширенные алгоритмы (2IL45) — Конспекты курса . ТУ Эйндховена. Архивировано (PDF) из оригинала 9 октября 2022 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

v т и Структуры данных и алгоритмы
Data structures	Array Associative array Binary search tree Fenwick tree Graph Hash table Heap Linked list Queue Segment tree Stack String Tree Trie
Algorithms	Backtracking Binary search Breadth-first search Brute-force search Depth-first search Divide and conquer Dynamic programming Graph traversal Fold Greedy Hash function Minimax Online Randomized Recursion Root-finding Sorting Streaming Sweep line String-searching Topological sorting
List of data structures List of algorithms