Вейвлет

Чтобы узнать о концепции физики, см. Волновой пакет .

Вейвлет — это волнообразное колебание , с амплитудой которая начинается с нуля, увеличивается или уменьшается, а затем возвращается к нулю один или несколько раз. Вейвлеты называются «краткими колебаниями». Установлена ​​таксономия вейвлетов, основанная на количестве и направлении их импульсов. Вейвлеты обладают особыми свойствами, которые делают их полезными для обработки сигналов .

Сейсмический вейвлет

Например, можно создать вейвлет с частотой средней до и короткой продолжительностью примерно в одну десятую секунды. Если этот вейвлет свернуть с сигналом , созданным при записи мелодии, то полученный сигнал будет полезен для определения того, когда в песне появилась средняя нота «до». Математически вейвлет коррелирует с сигналом, если часть сигнала аналогична. Корреляция лежит в основе многих практических вейвлет-приложений.

В качестве математического инструмента вейвлеты можно использовать для извлечения информации из многих видов данных, включая аудиосигналы и изображения. Для полного анализа данных необходимы наборы вейвлетов. «Дополнительные» вейвлеты разлагают сигнал без пропусков и перекрытий, так что процесс разложения математически обратим. Таким образом, наборы дополнительных вейвлетов полезны в алгоритмах сжатия/декомпрессии на основе вейвлетов , где желательно восстановить исходную информацию с минимальными потерями.

Формально это представление представляет собой вейвлет-серии представление в виде функции, интегрируемой с квадратом, относительно либо полного . ортонормированного набора базисных функций , либо сверхполного набора или фрейма векторного пространства для гильбертова пространства функций, интегрируемых с квадратом . Это достигается посредством согласованных государств .

В классической физике явление дифракции описывается принципом Гюйгенса-Френеля , который рассматривает каждую точку распространяющегося волнового фронта как совокупность отдельных сферических вейвлетов. Характерная картина изгиба наиболее выражена, когда волна от когерентного источника (например, лазера) встречает щель/апертуру, размер которой сопоставим с ее длиной волны . Это происходит из-за сложения или интерференции различных точек волнового фронта (или, что то же самое, каждого вейвлета), которые проходят по путям разной длины к регистрирующей поверхности. Несколько близко расположенных отверстий (например, дифракционная решетка ) могут привести к образованию сложной картины различной интенсивности.

Этимология

Слово « вейвлет» десятилетиями использовалось в цифровой обработке сигналов и разведочной геофизике. Эквивалентное французское слово ondelette, означающее «маленькая волна», использовалось Морле и Гроссманном в начале 1980-х годов.

Теория вейвлетов

Теория вейвлетов применима к нескольким предметам. Все вейвлет-преобразования можно рассматривать как формы частотно-временного представления для непрерывных (аналоговых) сигналов и поэтому они связаны с гармоническим анализом . Дискретное вейвлет-преобразование (непрерывное во времени) дискретного ( выборочного) сигнала с использованием дискретного времени наборов фильтров диадической (октавной полосы) конфигурации представляет собой вейвлет-аппроксимацию этого сигнала. Коэффициенты такого набора фильтров называются коэффициентами сдвига и масштабирования в номенклатуре вейвлетов. Эти наборы фильтров могут содержать фильтры либо с конечной импульсной характеристикой (FIR), либо с бесконечной импульсной характеристикой (IIR). Вейвлеты, образующие непрерывное вейвлет-преобразование (CWT), подчиняются принципу неопределенности анализа Фурье соответствующей теории выборки: учитывая сигнал с некоторым событием в нем, нельзя одновременно присвоить этому событию точную шкалу времени и частотной характеристики. Произведение неопределенностей шкалы времени и частотной характеристики имеет нижнюю границу. Таким образом, в масштабограммы непрерывного вейвлет-преобразования этого сигнала, такое событие отмечает целую область на плоскости шкалы времени, а не только одну точку. Кроме того, базы дискретных вейвлетов можно рассматривать в контексте других форм принципа неопределенности.

Вейвлет-преобразования в целом делятся на три класса: непрерывные, дискретные и на основе множественного разрешения.

преобразование (параметры непрерывного сдвига и

В непрерывных вейвлет-преобразованиях данный сигнал конечной энергии проецируется на непрерывное семейство частотных диапазонов (или аналогичные подпространства L ^п функциональное пространство L ² ( Р ) ). Например, сигнал может быть представлен в каждой полосе частот формы [ f , 2 f ] для всех положительных частот f > 0. Затем исходный сигнал может быть восстановлен путем подходящего интегрирования по всем результирующим частотным компонентам.

Полосы частот или подпространства (поддиапазоны) представляют собой масштабированные версии подпространства в масштабе 1. Это подпространство, в свою очередь, в большинстве ситуаций генерируется сдвигами одной производящей функции ψ в L ² ( R ), материнский вейвлет . Для примера полосы частот масштаба один [1, 2] эта функция равна

$$\psi (t)=2\,\operatorname {sinc} (2t)-\,\operatorname {sinc} (t)={\frac {\sin(2\pi t)-\sin(\pi t)}{\pi t}}$$

с (нормализованной) функцией sinc . Это, Мейер и два других примера материнских вейвлетов:

Мейер

Морле

Мексиканская шляпа

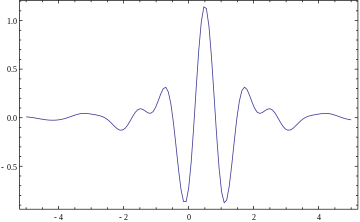Подпространство масштаба a или частотного диапазона [1/ a , 2/ a ] генерируется функциями (иногда называемыми дочерними вейвлетами )

$$\psi _{a,b}(t)={\frac {1}{\sqrt {a}}}\psi \left({\frac {t-b}{a}}\right),$$

где a положительное значение и определяет масштаб, а b — любое действительное число и определяет сдвиг. Пара ( a , b определяет точку в правой полуплоскости R ₊ × R. )

Тогда проекция функции x на подпространство масштаба a имеет вид

$$x_{a}(t)=\int _{\mathbb {R} }WT_{\psi }\{x\}(a,b)\cdot \psi _{a,b}(t)\,db$$

с вейвлет-коэффициентами

$$WT_{\psi }\{x\}(a,b)=\langle x,\psi _{a,b}\rangle =\int _{\mathbb {R} }x(t){\psi _{a,b}(t)}\,dt.$$

Для анализа сигнала x можно собрать вейвлет-коэффициенты в масштабограмму сигнала.

См. список некоторых непрерывных вейвлетов .

преобразования (дискретные параметры сдвига и масштабирования, непрерывные во времени

Вычислительно невозможно проанализировать сигнал, используя все вейвлет-коэффициенты, поэтому можно задаться вопросом, достаточно ли выбрать дискретное подмножество верхней полуплоскости, чтобы иметь возможность восстановить сигнал из соответствующих вейвлет-коэффициентов. Одной из таких систем является аффинная система для некоторых вещественных параметров a > 1, b > 0. Соответствующее дискретное подмножество полуплоскости состоит из всех точек ( a ^м , нет, а ^м ) m , n в Z. с Соответствующие дочерние вейвлеты теперь задаются как

$$\psi _{m,n}(t)={\frac {1}{\sqrt {a^{m}}}}\psi \left({\frac {t-nba^{m}}{a^{m}}}\right).$$

Достаточное условие восстановления любого сигнала x конечной энергии по формуле

$$x(t)=\sum _{m\in \mathbb {Z} }\sum _{n\in \mathbb {Z} }\langle x,\,\psi _{m,n}\rangle \cdot \psi _{m,n}(t)$$

заключается в том, что функции $\{\psi _{m,n}:m,n\in \mathbb {Z} \}$ образуют базис L ортонормированный ² ( Р ).

Дискретные вейвлет-преобразования на основе мультиразрешения (непрерывные

Вейвлет D4

В любом дискретном вейвлет-преобразовании существует только конечное число вейвлет-коэффициентов для каждой ограниченной прямоугольной области в верхней полуплоскости. Тем не менее, каждый коэффициент требует оценки интеграла. В особых ситуациях этой числовой сложности можно избежать, если масштабированные и сдвинутые вейвлеты образуют анализ с множественным разрешением . Это означает, что должна существовать вспомогательная функция , родительский вейвлет φ в L ² ( R ), и что a является целым числом. Типичный выбор — a = 2 и b = 1. Самая известная пара родительских и материнских вейвлетов — это 4-отводный вейвлет Добеши . Обратите внимание, что не каждый ортонормированный дискретный вейвлет-базис может быть связан с анализом с множественным разрешением; например, вейвлет Журна не допускает анализа с несколькими разрешениями.

Из вейвлетов матери и отца строятся подпространства

$$V_{m}=\operatorname {span} (\phi _{m,n}:n\in \mathbb {Z} ),{\text{ where }}\phi _{m,n}(t)=2^{-m/2}\phi (2^{-m}t-n)$$

$$W_{m}=\operatorname {span} (\psi _{m,n}:n\in \mathbb {Z} ),{\text{ where }}\psi _{m,n}(t)=2^{-m/2}\psi (2^{-m}t-n).$$

Отец вейвлет $V_{i}$ сохраняет свойства временной области, в то время как материнские вейвлеты $W_{i}$ сохраняет свойства частотной области.

Отсюда требуется, чтобы последовательность

$$\{0\}\subset \dots \subset V_{1}\subset V_{0}\subset V_{-1}\subset V_{-2}\subset \dots \subset L^{2}(\mathbb {R} )$$

формирует анализ L мультиразрешительный ² и что подпространства $\dots ,W_{1},W_{0},W_{-1},\dots$ являются ортогональными «разницами» указанной выше последовательности, то есть W _m является ортогональным дополнением V _m внутри подпространства V _{m −1} ,

$$V_{m}\oplus W_{m}=V_{m-1}.$$

По аналогии с теоремой о выборке можно заключить, что пространство V _m с расстоянием выборки 2 ^м более или менее покрывает полосу частот от 0 до 1/2 ^{м -1} . В качестве ортогонального дополнения W _m примерно покрывает полосу [1/2 ^{м −1} , 1/2 ^м ].

Из этих включений и отношений ортогональности, особенно $V_{0}\oplus W_{0}=V_{-1}$, следует существование последовательностей $h=\{h_{n}\}_{n\in \mathbb {Z} }$ и $g=\{g_{n}\}_{n\in \mathbb {Z} }$ которые удовлетворяют тождествам

$$g_{n}=\langle \phi _{0,0},\,\phi _{-1,n}\rangle$$

так что ${\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}$ и

$$h_{n}=\langle \psi _{0,0},\,\phi _{-1,n}\rangle$$

так что ${\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}$Второе тождество первой пары представляет собой уточняющее уравнение для родительского вейвлета φ. Обе пары тождеств составляют основу алгоритма быстрого вейвлет-преобразования .

Из многоразрешительного анализа выводится ортогональное разложение пространства L ² как

$$L^{2}=V_{j_{0}}\oplus W_{j_{0}}\oplus W_{j_{0}-1}\oplus W_{j_{0}-2}\oplus W_{j_{0}-3}\oplus \cdots$$

Для любого сигнала или функции $S\in L^{2}$ это дает представление в базисных функциях соответствующих подпространств в виде

$$S=\sum _{k}c_{j_{0},k}\phi _{j_{0},k}+\sum _{j\leq j_{0}}\sum _{k}d_{j,k}\psi _{j,k}$$

где коэффициенты

$$c_{j_{0},k}=\langle S,\phi _{j_{0},k}\rangle$$

и

$$d_{j,k}=\langle S,\psi _{j,k}\rangle .$$

-

Для обработки временных сигналов в реальном времени важно, чтобы вейвлет-фильтры не обращались к значениям сигналов из будущего, а также чтобы можно было получить минимальные временные задержки. Представления вейвлетов, причинных временем, были разработаны Szu et al. и Линдеберг, причем последний метод также включает в себя рекурсивную по времени реализацию, эффективно использующую память.

Материнский вейвлет

Для практических приложений и по соображениям эффективности предпочитают непрерывно дифференцируемые функции с компактной поддержкой в ​​качестве материнского (прототипного) вейвлета (функций). Однако для удовлетворения аналитических требований (в непрерывном WT) и в целом по теоретическим причинам вейвлет-функции выбираются из подпространства пространства $L^{1}(\mathbb {R} )\cap L^{2}(\mathbb {R} ).$ Это пространство измеримых по Лебегу функций, которые являются как абсолютно интегрируемыми , так и интегрируемыми с квадратом в том смысле, что

$$\int _{-\infty }^{\infty }|\psi (t)|\,dt<\infty$$

и

$$\int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt<\infty .$$

Находясь в этом пространстве, можно сформулировать условия нулевого среднего и единицы квадратичной нормы:

$$\int _{-\infty }^{\infty }\psi (t)\,dt=0$$

является условием нулевого среднего, а

$$\int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt=1$$

является условием квадратичной нормы один.

Чтобы ψ был вейвлетом для непрерывного вейвлет-преобразования (точные формулировки см. здесь), материнский вейвлет должен удовлетворять критерию допустимости (грубо говоря, своего рода полудифференцируемости), чтобы получить стабильно обратимое преобразование.

Для дискретного вейвлет-преобразования необходимо, по крайней мере, условие, что вейвлет-ряд является представлением идентичности в пространстве L. ² ( Р ). Большинство конструкций дискретного WT используют мультиразрешающий анализ , который определяет вейвлет с помощью масштабирующей функции. Эта масштабирующая функция сама по себе является решением функционального уравнения.

В большинстве ситуаций полезно ограничить ψ непрерывной функцией с большим числом M исчезающих моментов, т.е. для всех целых m < M

$$\int _{-\infty }^{\infty }t^{m}\,\psi (t)\,dt=0.$$

Материнский вейвлет масштабируется (или расширяется) в коэффициент a и переводится (или сдвигается) в коэффициент b , что дает (согласно исходной формулировке Морле):

$$\psi _{a,b}(t)={1 \over {\sqrt {a}}}\psi \left({t-b \over a}\right).$$

Для непрерывного WT пара ( a , b ) меняется во всей полуплоскости R ₊ × R ; для дискретного WT эта пара меняется на его дискретном подмножестве, которое также называется аффинной группой .

Эти функции часто ошибочно называют базисными функциями (непрерывного) преобразования. Фактически, как и в случае с непрерывным преобразованием Фурье, в непрерывном вейвлет-преобразовании нет основы. Частотно-временная интерпретация использует немного другую формулировку (по Дельпрату).

Ограничение:

1. ${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ когда a ₁ = a и b ₁ = b ,
2. $\Psi (t)$ имеет конечный интервал времени

время

Вейвлет-преобразование часто сравнивают с преобразованием Фурье , в котором сигналы представляются как сумма синусоид. Фактически преобразование Фурье можно рассматривать как частный случай непрерывного вейвлет-преобразования с выбором материнского вейвлета. $\psi (t)=e^{-2\pi it}$. Основное различие в целом заключается в том, что вейвлеты локализованы как по времени, так и по частоте, тогда как стандартное преобразование Фурье локализовано только по частоте . Кратковременное преобразование Фурье (STFT) похоже на вейвлет-преобразование тем, что оно также локализовано по времени и частоте, но существуют проблемы с компромиссом разрешения по частоте и времени.

В частности, предполагая прямоугольную область окна, можно думать о STFT как о преобразовании с немного другим ядром.

$$\psi (t)=g(t-u)e^{-2\pi it}$$

где $g(t-u)$ часто можно записать как ${\textstyle \operatorname {rect} \left({\frac {t-u}{\Delta _{t}}}\right)}$, где $\Delta _{t}$и u соответственно обозначают длину и временное смещение оконной функции. Используя теорему Парсеваля , можно определить энергию вейвлета как

$$E=\int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt={\frac {1}{2\pi }}\int _{-\infty }^{\infty }|{\hat {\psi }}(\omega )|^{2}\,d\omega$$

Отсюда квадрат временной опоры окна, смещенного на время u , определяется выражением

$$\sigma _{u}^{2}={\frac {1}{E}}\int |t-u|^{2}|\psi (t)|^{2}\,dt$$

и квадрат спектральной опоры окна, действующего на частоте $\xi$

$${\hat {\sigma }}_{\xi }^{2}={\frac {1}{2\pi E}}\int |\omega -\xi |^{2}|{\hat {\psi }}(\omega )|^{2}\,d\omega$$

Умножение на прямоугольное окно во временной области соответствует свертке с $\operatorname {sinc} (\Delta _{t}\omega )$функционируют в частотной области, что приводит к появлению ложных артефактов звона в коротких/локализованных временных окнах. С помощью преобразования Фурье с непрерывным временем $\Delta _{t}\to \infty$ и эта свертка выполняется с дельта-функцией в пространстве Фурье, что приводит к истинному преобразованию Фурье сигнала. $x(t)$. Оконной функцией может быть какой-либо другой аподизирующий фильтр , например, гауссов . Выбор оконной функции повлияет на ошибку аппроксимации относительно истинного преобразования Фурье.

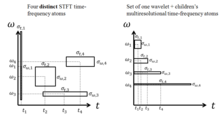
Произведение временной полосы пропускания ячейки данного разрешения не может быть превышено с помощью STFT. Все базовые элементы STFT поддерживают единую спектральную и временную поддержку для всех временных сдвигов или смещений, тем самым достигая одинакового разрешения во времени для более низких и более высоких частот. Разрешение определяется исключительно шириной выборки.

Напротив, свойства мультиразрешения вейвлет-преобразования обеспечивают большую временную поддержку для более низких частот, сохраняя при этом короткую временную ширину для более высоких частот за счет масштабирующих свойств вейвлет-преобразования. Это свойство расширяет традиционный частотно-временной анализ до анализа в масштабе времени.

Атомы частоты времени STFT (слева) и атомы шкалы времени DWT (справа). Частотно-временные атомы представляют собой четыре различные базисные функции, используемые для STFT (т.е. требуются четыре отдельных преобразования Фурье ). Атомы временной шкалы DWT достигают небольшой временной ширины для высоких частот и хорошей временной ширины для низких частот с помощью одного базисного набора преобразования.

Дискретное вейвлет-преобразование является менее сложным в вычислительном отношении и занимает время O( N ) по сравнению с O( N log N ) для быстрого преобразования Фурье . Это вычислительное преимущество не присуще преобразованию, но отражает выбор логарифмического деления частоты, в отличие от равноотстоящих друг от друга частотных делений БПФ (быстрого преобразования Фурье), которое использует те же базисные функции, что и ДПФ (дискретное преобразование Фурье). . Также важно отметить, что эта сложность применяется только тогда, когда размер фильтра не имеет отношения к размеру сигнала. Вейвлет без компактной поддержки , такой как вейвлет Шеннона, потребует O( N ² ). (Например, логарифмическое преобразование Фурье также существует со сложностью O( N ), но исходный сигнал должен быть логарифмически дискретизирован во времени, что полезно только для определенных типов сигналов. )

Определение вейвлета

Вейвлет (или семейство вейвлетов) можно определить различными способами:

Фильтр масштабирования

Ортогональный вейвлет полностью определяется масштабирующим фильтром – фильтром нижних частот с конечной импульсной характеристикой (FIR) длиной 2 N и суммой 1. В биортогональных вейвлетах определены отдельные фильтры разложения и реконструкции.

Для анализа с использованием ортогональных вейвлетов фильтр верхних частот рассчитывается как квадратурный зеркальный фильтр нижних частот, а фильтры реконструкции являются временными обратными фильтрами разложения.

Вейвлеты Добеши и Симлета могут быть определены с помощью масштабирующего фильтра.

Функция масштабирования

Вейвлеты определяются вейвлет-функцией ψ( t ) (т.е. материнским вейвлетом) и функцией масштабирования φ( t ) (также называемой родительским вейвлетом) во временной области.

Вейвлет-функция по сути представляет собой полосовой фильтр, масштабирование которого для каждого уровня уменьшает вдвое полосу пропускания. Это создает проблему: чтобы охватить весь спектр, потребуется бесконечное количество уровней. Функция масштабирования фильтрует самый низкий уровень преобразования и обеспечивает охват всего спектра. Видеть для подробного объяснения.

Для вейвлета с компактной поддержкой φ( t ) можно считать конечной по длине и эквивалентной масштабирующему фильтру g .

Вейвлеты Мейера можно определить с помощью функций масштабирования.

Вейвлет-функция

Вейвлет имеет только представление во временной области как вейвлет-функция ψ( t ).

Например, вейвлеты мексиканской шляпы могут быть определены с помощью вейвлет-функции. См. список нескольких непрерывных вейвлетов .

История

Развитие вейвлетов можно связать с несколькими отдельными направлениями мысли, начиная с работы Хаара в начале 20 века. Более поздняя работа Денниса Габора выявила атомы Габора (1946), которые устроены аналогично вейвлетам и применяются для аналогичных целей.

Заметный вклад в теорию вейвлетов с тех пор можно отнести к непрерывного открытию Цвейгом вейвлет-преобразования (CWT) в 1975 году (первоначально называвшегося кохлеарным преобразованием и открытого при изучении реакции уха на звук). Формулировка Пьера Гупийо, Гроссмана и Морле того, что сейчас известно как CWT (1982), ранняя работа Яна-Олова Стрёмберга по дискретным вейвлетам (1983), неортогональный 5/3-отвод Ле Галля – Табатабаи (LGT). блок фильтров с линейной фазой (1988), Ингрид Добеши Ортогональные вейвлеты с компактной поддержкой Биномиальная (1988), неортогональная структура множественного разрешения Малла (1989), Али Акансу ( QMF 1990), частотно-временная интерпретация CWT Натали Дельпра (1991), гармонический вейвлет Ньюленда преобразование (1993) и разделение множеств в иерархических деревьях (SPIHT), разработанное Амиром Саидом совместно с Уильямом А. Перлманом в 1996 году.

Стандарт JPEG 2000 разрабатывался с 1997 по 2000 год комитетом Объединенной группы экспертов по фотографии (JPEG) под председательством Тураджа Эбрахими (впоследствии президента JPEG). В отличие от алгоритма DCT, используемого в исходном формате JPEG , JPEG 2000 вместо этого использует алгоритмы дискретного вейвлет-преобразования (DWT). Он использует вейвлет-преобразование CDF 9/7 (разработанное Ингрид Добеши в 1992 году) для алгоритма сжатия с потерями и набор фильтров дискретного времени Ле Галля-Табатабай (LGT) 5/3 (разработанный Дидье Ле Галлем и Али Дж. Табатабаи в 1988 году) за алгоритм сжатия без потерь . Технология JPEG 2000 , включающая расширение Motion JPEG 2000 , была выбрана в качестве стандарта кодирования видео для цифрового кино в 2004 году.

Хронология

• Первый вейвлет ( Haar Wavelet ) Альфреда Хаара (1909)
• С 1970-х: Джордж Цвейг , Жан Морле , Алекс Гроссманн.
• С 1980-х: Ив Мейер , Дидье Ле Галль, Али Ж. Табатабай, Стивен Маллат , Ингрид Добеши , Рональд Койфман , Али Акансу , Виктор Викерхаузер
• С 1990-х годов: Натали Дельпрат, Ньюленд, Амир Саид, Уильям А. Перлман, Турадж Эбрахими, JPEG 2000.

Вейвлет-преобразования

Основная статья: Вейвлет-преобразование

Вейвлет — это математическая функция, используемая для разделения заданной функции или сигнала непрерывного времени на различные компоненты масштаба. Обычно каждому компоненту шкалы можно назначить частотный диапазон. Затем каждый компонент масштаба можно изучить с разрешением, соответствующим его масштабу. Вейвлет-преобразование — это представление функции вейвлетами. Вейвлеты представляют собой масштабированные и преобразованные копии (известные как «дочерние вейвлеты») осциллирующей формы конечной длины или быстро затухающей формы (известной как «материнский вейвлет»). Вейвлет-преобразования имеют преимущества перед традиционными преобразованиями Фурье для представления функций, имеющих разрывы и острые пики, а также для точного деконструирования и восстановления конечных, непериодических и /или нестационарных сигналов .

Вейвлет-преобразования подразделяются на дискретные вейвлет-преобразования (DWT) и непрерывные вейвлет-преобразования (CWT). Обратите внимание, что и DWT, и CWT являются преобразованиями непрерывного времени (аналоговыми). Их можно использовать для представления непрерывных (аналоговых) сигналов. CWT работают со всеми возможными масштабами и трансляциями, тогда как DWT используют определенное подмножество масштабов и значений перевода или сетку представления.

Существует большое количество вейвлет-преобразований, каждое из которых подходит для разных приложений. Полный список см. в списке преобразований, связанных с вейвлетами, но наиболее распространенные из них перечислены ниже:

• Непрерывное вейвлет-преобразование (CWT)
• Дискретное вейвлет-преобразование (DWT)
• Быстрое вейвлет-преобразование (FWT)
• Схема подъема и обобщенная схема подъема
• Вейвлет-разложение пакетов (WPD)
• Стационарное вейвлет-преобразование (SWT)
• Дробное преобразование Фурье (FRFT)
• Дробное вейвлет-преобразование (FRWT)

Обобщенные преобразования

Существует ряд обобщенных преобразований, частным случаем которых является вейвлет-преобразование. Например, Йосеф Джозеф Сегман ввел масштаб в группу Гейзенберга , породив пространство непрерывного преобразования, которое является функцией времени, масштаба и частоты. CWT представляет собой двумерный срез полученного трехмерного объема в масштабе времени и частоте.

Другим примером обобщенного преобразования является преобразование лирплета, в котором CWT также является двумерным срезом преобразования лирплета.

Важная область применения обобщенных преобразований включает системы, в которых решающее значение имеет высокое разрешение по частоте. Например, темнопольные электронно-оптические преобразования, промежуточные между прямым и обратным пространством, широко используются при гармоническом анализе кластеризации атомов, т. е. при исследовании кристаллов и кристаллических дефектов . Теперь, когда трансмиссионные электронные микроскопы способны предоставлять цифровые изображения с пикометрической информацией об атомной периодичности в наноструктурах всех видов, диапазон распознавания образов и напряжение / метрология приложения для промежуточных преобразований с высоким частотным разрешением (например, кисти и риджлеты ) быстро растет.

Дробное вейвлет-преобразование (FRWT) представляет собой обобщение классического вейвлет-преобразования в областях дробного преобразования Фурье. Это преобразование способно одновременно предоставлять информацию во временной и дробной области и представлять сигналы в плоскости дробно-временной частоты.

Приложения

Обычно аппроксимация DWT используется для сжатия данных , если сигнал уже дискретизирован, а CWT — для анализа сигнала . Таким образом, приближение DWT обычно используется в технике и информатике. и CWT в научных исследованиях.

Как и некоторые другие преобразования, вейвлет-преобразования можно использовать для преобразования данных, а затем кодирования преобразованных данных, что приводит к эффективному сжатию. Например, JPEG 2000 — это стандарт сжатия изображений, использующий биортогональные вейвлеты. Это значит, что хотя кадр и переполнен, но это плотный кадр (см. типы кадров векторного пространства ), и для анализа и синтеза используются одни и те же функции кадра (за исключением сопряжения в случае комплексных вейвлетов), т.е. , как при прямом, так и при обратном преобразовании. Подробнее см. вейвлет-сжатие .

Связанное использование — сглаживание/шумоподавление данных на основе порогового значения вейвлет-коэффициента, также называемого вейвлет-сжатием. Путем адаптивного определения порога вейвлет-коэффициентов, которые соответствуют нежелательным частотным компонентам, могут быть выполнены операции сглаживания и/или шумоподавления.

Вейвлет-преобразования также начинают использоваться в коммуникационных приложениях. Wavelet OFDM — это базовая схема модуляции, используемая в HD-PLC ( технология связи по линиям электропередачи, разработанная Panasonic ), а также в одном из дополнительных режимов, включенных в стандарт IEEE 1901 . Вейвлет OFDM может достигать более глубоких вырезов, чем традиционный FFT OFDM, а вейвлет OFDM не требует защитного интервала (который обычно представляет собой значительные накладные расходы в системах FFT OFDM).

Как представление сигнала

Часто сигналы можно представить в виде суммы синусоид. Однако рассмотрим прерывистый сигнал с резким скачком; этот сигнал все еще можно представить как сумму синусоид, но требуется бесконечное число, что является наблюдением, известным как феномен Гиббса . Таким образом, для этого требуется бесконечное число коэффициентов Фурье, что непрактично для многих приложений, таких как сжатие. Вейвлеты более полезны для описания этих сигналов с разрывами из-за их поведения, локализованного во времени (как преобразования Фурье, так и вейвлет-преобразования локализованы по частоте, но вейвлеты обладают дополнительным свойством локализации по времени). Из-за этого многие типы сигналов на практике могут быть неразреженными в области Фурье, но очень разреженными в области вейвлетов. Это особенно полезно при реконструкции сигналов, особенно в популярной в последнее время области измерения сжатых данных . (Обратите внимание, что кратковременное преобразование Фурье (STFT) также локализовано во времени и частоте, но часто возникают проблемы с компромиссом разрешения частоты и времени. Вейвлеты являются лучшим представлением сигнала из-за мультиразрешительный анализ .)

Это объясняет, почему вейвлет-преобразования в настоящее время применяются для огромного количества приложений, часто заменяя обычное преобразование Фурье . Этот сдвиг парадигмы произошел во многих областях физики, включая молекулярную динамику , теорию хаоса , ab initio расчеты , астрофизика , гравитационных волн , анализ данных о переходных процессах в матрице плотности локализация , сейсмология , оптика , турбулентность и квантовая механика . Это изменение также произошло в обработке изображений , ЭЭГ , ЭМГ , ЭКГ Анализы , ритмы мозга , ДНК анализ белков , анализ , климатология , анализ сексуальной реакции человека, общая обработка сигналов , распознавание речи , акустика, вибрационные сигналы, компьютерная графика , мультифрактальный анализ и разреженное кодирование . В компьютерном зрении и обработке изображений понятие представления масштабного пространства и операторов производной Гаусса рассматривается как каноническое многомасштабное представление.

Вейвлетное шумоподавление

Шумоподавление сигнала с помощью порогового значения вейвлет-преобразования

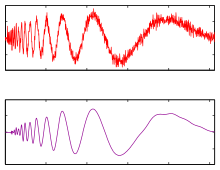
Предположим, мы измеряем зашумленный сигнал $x=s+v$, где $s$ представляет сигнал и $v$представляет собой шум. Предполагать $s$ имеет разреженное представление в определенном вейвлет-базисе и $v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)$

Пусть вейвлет-преобразование $x$ быть $y=W^{T}x=W^{T}s+W^{T}v=p+z$, где $p=W^{T}s$ - вейвлет-преобразование компонента сигнала и $z=W^{T}v$ — вейвлет-преобразование шумовой составляющей.

Большинство элементов в $p$ равны 0 или близки к 0, и $z\ \sim \ \ {\mathcal {N}}(0,\,\sigma ^{2}I)$

С $W$ортогональна, задача оценки сводится к восстановлению сигнала в гауссовском шуме . Как $p$ разрежена, один из методов состоит в применении модели гауссовой смеси для $p$.

Предположим, что предварительно $p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})$, где $\sigma _{1}^{2}$ - дисперсия «значимых» коэффициентов и $\sigma _{2}^{2}$ – дисперсия «незначимых» коэффициентов.

Затем ${\tilde {p}}=E(p/y)=\tau (y)y$, $\tau (y)$ называется коэффициентом усадки, который зависит от предыдущих отклонений $\sigma _{1}^{2}$ и $\sigma _{2}^{2}$. При установке коэффициентов, которые падают ниже порога сжатия, на ноль, после применения обратного преобразования ожидаемо небольшое количество сигнала теряется из-за предположения о разреженности. Ожидается, что более крупные коэффициенты будут в первую очередь представлять сигнал из-за разреженности, и статистически ожидается, что очень небольшая часть сигнала, хотя и большая часть шума, будет представлена ​​в таких коэффициентах с более низкой величиной... поэтому ожидается, что операция обнуления будет удалить большую часть шума и не так много сигнала. Обычно коэффициенты над порогом не изменяются в ходе этого процесса. Некоторые алгоритмы шумоподавления на основе вейвлетов также могут ослаблять более крупные коэффициенты на основе статистической оценки количества шума, которое, как ожидается, будет удалено в результате такого ослабления.

Наконец, примените обратное вейвлет-преобразование, чтобы получить ${\tilde {s}}=W{\tilde {p}}$

климатическая

Агарвал и др. предложенный расширенный линейный метод на основе вейвлетов и нелинейный методы построения и исследования климата как сложных сетей в разных временных масштабах. Климатические сети, построенные с использованием наборов данных ТПО в разных временных масштабах, показали, что многомасштабный анализ климатических процессов на основе вейвлетов обещает лучшее понимание динамики системы, которую можно упустить, если процессы анализируются только в одном временном масштабе.

Список вейвлетов

Дискретные вейвлеты

• Бейлкин (18)
• Вейвлет Мура
• Биортогональные почти койфлетные вейвлеты (BNC)
• Койфлет (6, 12, 18, 24, 30)
• Вейвлет Коэна-Добеши-Фово (иногда называемый CDF N/P или биортогональными вейвлетами Добеши)
• Вейвлет Добеши (2, 4, 6, 8, 10, 12, 14, 16, 18, 20 и т. д.)
• Биномиальный QMF (также называемый вейвлетом Добеши)
• Вейвлет для волос
• вейвлет Матье
• Вейвлет Лежандра
• Вейвлет Вилласенор
• Символ

Непрерывные вейвлеты

Реальная стоимость

• Бета-вейвлет
• Эрмитовский вейвлет
• вейвлет Мейера
• Мексиканская шляпа-вейвлет
• Пуассоновский вейвлет
• Шеннонский вейвлет
• Сплайновый вейвлет
• Вейвлет Стрёмберга

Комплексное значение

• Сложный вейвлет мексиканской шляпы
• вейвлет fbsp
• Вейвлет Морле
• Шеннонский вейвлет
• Модифицированный вейвлет Морле

См. также

• Преобразование чирплета
• Курвлет
• Цифровое кино
• Уменьшение размеров
• Банки фильтров
• Преобразования, связанные с Фурье
• Фрактальное сжатие
• Дробное преобразование Фурье
• Вейвлет Габора § Вейвлет-пространство
• Принцип Гюйгенса – Френеля (физические вейвлеты)
• JPEG 2000
• Спектральный анализ методом наименьших квадратов для вычисления периодичности любых данных, включая неравномерно расположенные.
• Мультиразрешительный анализ
• Шумлет
• Неразделимый вейвлет
• Масштабировать пространство
• Масштабированная корреляция
• Шерлет
• Кратковременное преобразование Фурье
• Спектрограмма
• Сверхширокополосное радио - передает вейвлеты

Дальнейшее чтение

• Хаар А., К теории ортогональных функциональных систем , Mathematical Annals, 69 , стр. 331–371, 1910.
• Ингрид Добеши , Десять лекций по вейвлетам , Общество промышленной и прикладной математики, 1992, ISBN   0-89871-274-2 .
• Али Акансу и Ричард Хаддад, Разложение сигнала с несколькими разрешениями: преобразования, поддиапазоны, вейвлеты , Academic Press, 1992, ISBN   0-12-047140-X .
• П. П. Вайдьянатан , Многоскоростные системы и банки фильтров , Prentice Hall, 1993, ISBN   0-13-605718-7 .
• Джеральд Кайзер, Дружественное руководство по вейвлетам , Биркхаузер, 1994, ISBN   0-8176-3711-7 .
• Младен Виктор Викерхаузер, Адаптированный вейвлет-анализ от теории к программному обеспечению , AK Peters Ltd, 1994, ISBN   1-56881-041-5 .
• Мартин Веттерли и Елена Ковачевич, «Вейвлеты и кодирование поддиапазонов», Прентис Холл, 1995 г., ISBN   0-13-097080-8 .
• Барбара Берк Хаббард , «Мир согласно вейвлетам: история создания математической техники», AK Peters Ltd, 1998, ISBN   1-56881-072-5 , ISBN   978-1-56881-072-0 .
• Стефан Малла , «Вейвлет-тур по обработке сигналов», 2-е издание, Academic Press, 1999, ISBN   0-12-466606-X .
• Дональд Б. Персиваль и Эндрю Т. Уолден, Вейвлет-методы для анализа временных рядов , издательство Кембриджского университета, 2000 г., ISBN   0-521-68508-7 .
• Рамазан Генчай, Фарук Сельчук и Брэндон Уитчер, Введение в вейвлеты и другие методы фильтрации в финансах и экономике , Academic Press, 2001, ISBN   0-12-279670-5 .
• Пол С. Аддисон, Иллюстрированное руководство по вейвлет-преобразованию , Институт физики , 2002 г., ISBN   0-7503-0692-0 .
• Б. Боашаш, редактор, «Анализ и обработка частотно-временных сигналов – всеобъемлющий справочник», Elsevier Science, Оксфорд, 2003 г., ISBN   0-08-044335-4 .
• Тони Ф. Чан и Джеки (Цзяньхун) Шен , Обработка и анализ изображений – вариационные, PDE, вейвлет-методы и стохастические методы , Общество прикладной математики, ISBN   0-89871-589-X (2005).
• Пресс, WH; Теукольский, С.А.; Феттерлинг, WT; Фланнери, BP (2007), «Раздел 13.10. Вейвлет-преобразования» , Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN  978-0-521-88068-8 , заархивировано из оригинала 11 августа 2011 г. , получено 13 августа 2011 г.
• «Как вейвлеты позволяют исследователям преобразовывать и понимать данные» . Журнал Кванта . 13 октября 2021 г. Проверено 20 октября 2021 г.

Внешние ссылки

• «Вейвлет-анализ» , Математическая энциклопедия , EMS Press , 2001 [1994]
• 1-й симпозиум NJIT по вейвлетам (30 апреля 1990 г.) (Первая конференция вейвлетов в США)
• Биномиальные вейвлеты Добеши-QMF
• Вейвлеты Гилберта Стрэнга, американского ученого 82 (1994) 250–255. (Очень короткое и превосходное введение)
• Курс по вейвлетам в Калифорнийском университете в Санта-Барбаре, 2004 г.
• Вейвлеты для детей (файл PDF) (Вводный (для очень умных детей!))
• УИТС: Где Старлетка? Словарь десятков вейвлетов и терминов, связанных с вейвлетами, оканчивающихся на -let, от активных до x-лет, через бандлеты, контурлеты, кривые, шумлеты, клинья.
• Вейвлет-преобразование дробного сплайна описывает дробное вейвлет-преобразование, основанное на дробных b-сплайнах.
• «Панорама многомасштабных геометрических представлений, переплетения пространственной, направленной и частотной избирательности» представляет собой учебное пособие по двумерным ориентированным вейвлетам и связанным с ними геометрическим многомасштабным преобразованиям.
• Краткое введение в вейвлеты Рене Пушингера
• Действительно дружелюбное руководство по вейвлетам Клеменса Валенса
• «Как вейвлеты позволяют исследователям преобразовывать и понимать данные» . Журнал Кванта . 13 октября 2021 г. Проверено 20 октября 2021 г.