Банк фильтров

При обработке сигналов банк фильтров (или банк фильтров ) представляет собой массив полосовых фильтров , который разделяет входной сигнал на несколько компонентов, каждый из которых несет поддиапазон исходного сигнала. Одним из применений банка фильтров является графический эквалайзер , который может по-разному ослаблять компоненты и повторно объединять их в модифицированную версию исходного сигнала. Процесс разложения, выполняемый банком фильтров, называется анализом (имеется в виду анализ сигнала по его компонентам в каждом поддиапазоне); Результат анализа называется сигналом поддиапазона с таким количеством поддиапазонов, сколько фильтров имеется в банке фильтров. Процесс реконструкции называется синтезом , что означает восстановление полного сигнала, полученного в результате процесса фильтрации.

В цифровой обработке сигналов термин «банк фильтров» также обычно применяется к банку приемников. Разница в том, что приемники также преобразуют поддиапазоны с понижением частоты до низкой центральной частоты, которую можно повторно дискретизировать с пониженной скоростью. Того же результата иногда можно достичь за счет недостаточной дискретизации полосовых поддиапазонов.

Другое применение банков фильтров — сжатие сигналов , когда одни частоты более важны, чем другие. После разложения важные частоты могут быть закодированы с высоким разрешением. Небольшие различия на этих частотах значительны, и кодирования необходимо использовать схему , сохраняющую эти различия. С другой стороны, менее важные частоты не обязательно должны быть точными. Можно использовать более грубую схему кодирования, даже если некоторые более мелкие (но менее важные) детали будут потеряны при кодировании.

Вокодер использует банк фильтров для определения информации об амплитуде поддиапазонов сигнала модулятора (например , голоса) и использует их для управления амплитудой поддиапазонов несущего сигнала (например, выхода гитары или синтезатора). тем самым накладывая динамические характеристики модулятора на несущую.

Описание реализации и работы банка фильтров взвешенного перекрытия (WOLA). Обертывание циклического входного буфера используется для компенсации разрывов фазы, вызванных отсутствием истинной привязки времени для преобразования Фурье (DFT).

Некоторые банки фильтров работают почти полностью во временной области, используя серию фильтров, таких как квадратурные зеркальные фильтры или алгоритм Герцеля, для разделения сигнала на более мелкие полосы.Другие банки фильтров используют быстрое преобразование Фурье (БПФ).

Банки фильтров БПФ

Банк приемников может быть создан путем выполнения последовательности БПФ на перекрывающихся сегментах входного потока данных. К каждому сегменту применяется весовая функция (она же оконная функция ) для управления формой частотных характеристик фильтров. Чем шире форма, тем чаще необходимо выполнять БПФ, чтобы удовлетворить критериям выборки Найквиста . Для фиксированной длины сегмента степень перекрытия определяет, как часто выполняется БПФ (и наоборот). Кроме того, чем шире форма фильтров, тем меньше фильтров требуется для охвата входной полосы пропускания. Устранение ненужных фильтров (т.е. прореживание частоты) эффективно осуществляется путем обработки каждого взвешенного сегмента как последовательности меньших блоков , а БПФ выполняется только для суммы блоков. Это называется БПФ с перекрытием весов (WOLA) и взвешенным БПФ с предварительной суммой . (см. § Выборка DTFT )

Особый случай возникает, когда по замыслу длина блоков является целым числом, кратным интервалу между БПФ. Тогда банк фильтров БПФ можно описать в терминах одной или нескольких структур многофазных фильтров, в которых фазы рекомбинируются с помощью БПФ вместо простого суммирования. Количество блоков на сегмент — это длина импульсной характеристики (или глубина ) каждого фильтра. Вычислительная эффективность БПФ и многофазных структур на процессоре общего назначения идентична.

Синтез (т. е. рекомбинация выходных сигналов нескольких приемников) по сути заключается в повышении частоты дискретизации каждого из них со скоростью, соизмеримой с общей создаваемой полосой пропускания, переводе каждого канала на его новую центральную частоту и суммировании потоков выборок. В этом контексте интерполяционный фильтр, связанный с повышающей дискретизацией, называется фильтром синтеза . Чистая частотная характеристика каждого канала является продуктом фильтра синтеза с частотной характеристикой банка фильтров ( фильтра анализа ). В идеале сумма частотных характеристик соседних каналов равна постоянному значению на каждой частоте между центрами каналов. Это состояние известно как идеальная реконструкция .

Банки фильтров как частотно-временные распределения

При частотно-временной обработке сигналов банк фильтров представляет собой специальное квадратичное частотно-временное распределение (TFD), которое представляет сигнал в совместной частотно-временной области . Оно связано с распределением Вигнера-Вилля двумерной фильтрацией, которая определяет класс квадратичных (или билинейных) частотно-временных распределений . Набор фильтров и спектрограмма — два простейших способа создания квадратичного TFD; по сути они похожи, поскольку одна (спектрограмма) получается путем разделения временной области на срезы и последующего преобразования Фурье, а другая (банк фильтров) получается путем разделения частотной области на срезы, образующие полосовые фильтры, которые возбуждаются по анализируемому сигналу.

Многоскоростной банк фильтров

Банк многоскоростных фильтров делит сигнал на несколько поддиапазонов, которые можно анализировать с разными скоростями, соответствующими ширине полосы частот. Реализация использует понижающую дискретизацию (децимацию) и повышающую дискретизацию (расширение) . См. § Свойства дискретного преобразования Фурье и § Свойства Z-преобразования для получения дополнительной информации о влиянии этих операций в областях преобразования.

Узкий фильтр нижних частот

Можно определить узкий фильтр нижних частот как фильтр нижних частот с узкой полосой пропускания.Чтобы создать многоскоростной узкий КИХ-фильтр нижних частот, можно заменить неизменяемый во времени КИХ-фильтр фильтром сглаживания нижних частот и дециматором, а также интерполятором и фильтром защиты от изображения нижних частот.Таким образом, результирующая многоскоростная система представляет собой изменяющийся во времени линейно-фазовый фильтр через дециматор и интерполятор.Фильтр нижних частот состоит из двух многофазных фильтров: одного для дециматора и одного для интерполятора.

Банк фильтров делит входной сигнал $x\left(n\right)$ в набор сигналов $x_{1}(n),x_{2}(n),x_{3}(n),...$. Таким образом, каждый из генерируемых сигналов соответствует отдельной области спектра. $x\left(n\right)$.В этом процессе регионы могут перекрываться (или нет, в зависимости от приложения).

Сгенерированные сигналы $x_{1}(n),x_{2}(n),x_{3}(n),...$ может быть сгенерирован с помощью набора полосовых фильтров с полосами пропускания ${\rm {BW_{1},BW_{2},BW_{3},...}}$ и центральные частоты $f_{c1},f_{c2},f_{c3},...$(соответственно).Банк многоскоростных фильтров использует один входной сигнал, а затем создает несколько выходных сигналов путем фильтрации и субдискретизации.Чтобы разделить входной сигнал на два или более сигналов, можно использовать систему анализа-синтеза.

Сигнал будет разделен с помощью четырех фильтров. $H_{k}(z)$ для k =0,1,2,3 на 4 полосы с одинаковой шириной полосы (в банке анализа), а затем каждый подсигнал прореживается в 4 раза.В каждой полосе, разделив сигнал на каждую полосу, мы получим разные характеристики сигнала.

В разделе синтеза фильтр восстановит исходный сигнал:Сначала выполняется повышающая дискретизация 4 субсигналов на выходе процессора в 4 раза, а затем фильтрация с помощью 4 фильтров синтеза. $F_{k}(z)$ для к = 0,1,2,3.Наконец, добавляются выходные данные этих четырех фильтров.

Статистически оптимизированный банк фильтров (банк собственных фильтров)

Структура банка фильтров с дискретным временем позволяет включать в проект функции, зависящие от желаемого входного сигнала, в дополнение к более традиционному свойству идеальной реконструкции. Теоретико-информационные особенности, такие как максимальное сжатие энергии, идеальная декорреляция сигналов поддиапазонов и другие характеристики для заданной входной ковариационной/корреляционной структуры, включены в разработку оптимальных банков фильтров. Эти банки фильтров напоминают зависимое от сигнала преобразование Карунена – Лоэва (KLT), которое является оптимальным блочным преобразованием, в котором длина L базисных функций (фильтров) и размерность подпространства M одинаковы.

Многомерные банки фильтров

Решетка квинкунса

Многомерная фильтрация , понижающая и повышающая дискретизация являются основными частями многоскоростных систем и банков фильтров.

Полный банк фильтров состоит из стороны анализа и синтеза.Банк фильтров анализа делит входной сигнал на разные поддиапазоны с разными частотными спектрами.Часть синтеза повторно собирает сигналы различных поддиапазонов и генерирует восстановленный сигнал.Двумя основными строительными блоками являются дециматор и расширитель. Например, вход делится на четыре направленных поддиапазона, каждый из которых покрывает одну из клиновидных частотных областей. В 1D-системах дециматоры M-кратности сохраняют только те выборки, которые кратны M, и отбрасывают остальные. в то время как в многомерных системах дециматоры представляют собой D × D. невырожденную целочисленную матрицу размера он учитывает только те выборки, которые находятся на решетке, созданной дециматором. Обычно используемый дециматор - это дециматор Квинкунса, решетка которого генерируется из матрицы Квинкунса , которая определяется формулой ${\begin{bmatrix}\;\;\,1&1\\-1&1\end{bmatrix}}$

Решетка квинконса, порожденная матрицей квинконса, такая, как показано; часть синтеза двойственна части анализа.Банки фильтров можно анализировать с точки зрения частотной области с точки зрения разложения и реконструкции поддиапазонов. Однако не менее важна интерпретация наборов фильтров в гильбертовом пространстве , которая играет ключевую роль в геометрических представлениях сигналов.Для универсального K -канала с фильтрами анализа. банка фильтров $\left\{h_{k}[n]\right\}_{k=1}^{K}$, фильтры синтеза $\left\{g_{k}[n]\right\}_{k=1}^{K}$и матрицы выборки $\left\{M_{k}[n]\right\}_{k=1}^{K}$.На стороне анализа мы можем определить векторы в $\ell ^{2}(\mathbf {Z} ^{d})$ как

$\varphi _{k,m}[n]{\stackrel {\rm {def}}{=}}h_{k}^{*}[M_{k}m-n]$,

каждый индекс по двум параметрам: $1\leq k\leq K$ и $m\in \mathbf {Z} ^{2}$.

Аналогично для фильтров синтеза $g_{k}[n]$ мы можем определить $\psi _{k,m}[n]{\stackrel {\rm {def}}{=}}g_{k}^{*}[M_{k}m-n]$.

Учитывая определение сторон анализа/синтеза, мы можем убедиться, что $c_{k}[m]=\langle x[n],\varphi _{k,m}[n]\rangle$ и для части реконструкции:

${\hat {x}}[n]=\sum _{1\leq k\leq K,m\in \mathbf {Z} ^{2}}c_{k}[m]\psi _{k,m}[n]$.

Другими словами, банк фильтров анализа вычисляет внутреннее произведение входного сигнала и вектора из набора анализа. Более того, восстановленный сигнал представляет собой комбинацию векторов из набора синтеза и коэффициентов комбинации вычисленных внутренних продуктов, что означает, что

${\hat {x}}[n]=\sum _{1\leq k\leq K,m\in \mathbf {Z} ^{2}}\langle x[n],\varphi _{k,m}[n]\rangle \psi _{k,m}[n]$

Если при разложении и последующей реконструкции потерь нет, набор фильтров называется идеальной реконструкцией . (в этом случае мы имели бы $x[n]={\hat {x[n]}}$. На рисунке показан общий многомерный набор фильтров с N общей матрицей выборки M. каналами и Часть анализа преобразует входной сигнал $x[n]$ в N отфильтрованных и субдискретизированных выходных данных $y_{j}[n],$ $j=0,1,...,N-1$.Часть синтеза восстанавливает исходный сигнал из $y_{j}[n]$ путем повышения дискретизации и фильтрации.Этот тип настройки используется во многих приложениях, таких как кодирование поддиапазонов , многоканальный сбор данных и дискретные вейвлет-преобразования .

Наборы фильтров идеальной реконструкции

Мы можем использовать многофазное представление, поэтому входной сигнал $x[n]$ может быть представлен вектором его многофазных компонентов $x(z){\stackrel {\rm {def}}{=}}(X_{0}(z),...,X_{|M|-1}(z))^{T}$. Обозначим $y(z){\stackrel {\rm {def}}{=}}(Y_{0}(z),...,Y_{|N|-1}(z))^{T}.$
Итак, у нас было бы $y(z)=H(z)x(z)$, где $H_{i,j}(z)$ обозначает j -ю многофазную составляющую фильтра $H_{i}(z)$.

Аналогично, для выходного сигнала мы будем иметь ${\hat {x}}(z)=G(z)y(z)$, где ${\hat {x}}(z){\stackrel {\rm {def}}{=}}({\hat {X}}_{0}(z),...,{\hat {X}}_{|M|-1}(z))^{T}$. Также G является матрицей, где $G_{i,j}(z)$ обозначает i-й полифазный компонент j-го синтезафильтр Gj(z).

Банк фильтров имеет идеальную реконструкциюесли $x(z)={\hat {x}}(z)$ для любого ввода или эквивалентно $I_{|M|}=G(z)H(z)$ что означает, что G(z) является левой инверсией H(z).

Многомерная конструкция фильтра

Банк 1D-фильтров

Банк 2D-фильтров

Банки одномерных фильтров до сих пор хорошо развиты. Однако многие сигналы, такие как изображение, видео, трехмерный звук, радар, гидролокатор, являются многомерными и требуют разработки многомерных банков фильтров.

В связи с быстрым развитием коммуникационных технологий системе обработки сигналов требуется больше места для хранения данных во время обработки, передачи и приема. Чтобы уменьшить объем обрабатываемых данных, сэкономить место и снизить сложность, для достижения этих целей были введены методы многоскоростной выборки. Банки фильтров можно использовать в различных областях, таких как кодирование изображений, кодирование голоса, радар и т. д.

Многие проблемы одномерных фильтров были хорошо изучены, и исследователи предложили множество подходов к проектированию банка одномерных фильтров. Однако остается еще много проблем проектирования многомерных наборов фильтров, которые необходимо решить. Некоторые методы могут плохо реконструировать сигнал, некоторые методы сложны и трудны для реализации.

Самый простой подход к созданию многомерного банка фильтров — это каскадирование одномерных банков фильтров в виде древовидной структуры, где матрица прореживания является диагональной, а данные обрабатываются в каждом измерении отдельно. Такие системы называются сепарабельными. Однако область поддержки банков фильтров может быть неотделима. В этом случае проектирование банка фильтров усложняется. В большинстве случаев мы имеем дело с неразделимыми системами.

Банк фильтров состоит из этапа анализа и этапа синтеза. Каждая ступень состоит из набора фильтров, работающих параллельно. Проектирование банка фильтров — это проектирование фильтров на стадиях анализа и синтеза. Фильтры анализа делят сигнал на перекрывающиеся или неперекрывающиеся поддиапазоны в зависимости от требований приложения. Фильтры синтеза должны быть спроектированы так, чтобы восстанавливать входной сигнал обратно из поддиапазонов при объединении выходов этих фильтров. Обработка обычно выполняется после этапа анализа. Эти банки фильтров могут быть спроектированы как с бесконечной импульсной характеристикой (IIR) или с конечной импульсной характеристикой (FIR).Чтобы снизить скорость передачи данных, на этапах анализа и синтеза выполняются понижающая и повышающая дискретизация соответственно.

Существующие подходы

Ниже приведены несколько подходов к проектированию многомерных банков фильтров. Для получения более подробной информации, пожалуйста, проверьте ОРИГИНАЛЬНЫЕ ссылки.

Многомерные банки фильтров идеальной реконструкции

Когда необходимо восстановить разделенный сигнал обратно в исходный, можно использовать банки фильтров идеальной реконструкции (PR).

Пусть H( z ) будет передаточной функцией фильтра. Размер фильтра определяется как порядок соответствующего полинома в каждом измерении. Симметрия или антисимметрия полинома определяет свойство линейной фазы соответствующего фильтра и связана с его размером.Как и в случае 1D, термин совмещения A(z) и передаточная функция T(z) для двухканального банка фильтров:

А( z )=1/2(Ч ₀ (- z ) F ₀ ( z ) + Ч ₁ (- z ) F ₁ ( z ));Т( z )=1/2(Ч ₀ ( z ) F ₀ ( z )+Ч ₁ ( z ) F ₁ ( z )),где H ₀ и H ₁ - фильтры разложения, а F ₀ и F ₁ - фильтры восстановления.

Входной сигнал может быть идеально восстановлен, если исключить псевдоним и T( z ) равен моному. Таким образом, необходимым условием является то, что T'( z ) в целом симметричен и имеет нечетный размер.

Линейно-фазовые PR-фильтры очень полезны для обработки изображений. Этот двухканальный набор фильтров относительно легко реализовать. Но двух каналов иногда бывает недостаточно. Двухканальные банки фильтров могут быть каскадно соединены для создания многоканальных банков фильтров.

Многомерные банки направленных фильтров и поверхности

Банки фильтров многомерного анализа

M-мерные банки направленных фильтров (MDFB) — это семейство банков фильтров, которые могут обеспечить направленное разложение произвольных M-мерных сигналов с помощью простой и эффективной древовидной структуры. Он имеет множество отличительных свойств, таких как: направленная декомпозиция, эффективное построение дерева, угловое разрешение и идеальная реконструкция.В общем M-мерном случае идеальными частотными носителями MDFB являются гиперпирамиды на основе гиперкуба. Первый уровень разложения для MDFB достигается с помощью N-канального непрореженного банка фильтров, компонентными фильтрами которого являются MD-фильтры в форме «песочных часов», выровненные по осям w ₁ ,...,w _M соответственно. После этого входной сигнал дополнительно разлагается с помощью серии двумерных банков шахматных фильтров с итеративной повторной выборкой IRC _li. ^{( Что )} (i=2,3,...,M), где IRC _li ^{( Что )} работает с двумерными срезами входного сигнала, представленными парой измерений (n ₁ ,ni ₎ , а верхний индекс (Li) означает уровни разложения для i-го банка фильтров уровня. Обратите внимание, что, начиная со второго уровня, мы прикрепляем банк фильтров IRC к каждому выходному каналу предыдущего уровня, и, следовательно, весь фильтр имеет в общей сложности 2 ^{( Л ₁ +...+ Л _Н )} выходные каналы.

Многомерные банки фильтров с передискретизацией

Банки фильтров многомерного синтеза

Банки фильтров с передискретизацией — это банки многоскоростных фильтров, в которых количество выходных выборок на этапе анализа больше, чем количество входных выборок. Предлагается для надежных приложений. Одним из конкретных классов банков фильтров с передискретизацией являются банки фильтров без субдискретизации без понижающей или повышающей дискретизации. Идеальное условие восстановления для банка фильтров с передискретизацией может быть сформулировано как матричная обратная задача в многофазной области.

Для банка фильтров с передискретизацией IIR идеальная реконструкция была изучена в Воловиче. и Кайлат. в контексте теории управления. В то время как для банка фильтров FIR с передискретизацией мы должны использовать разные стратегии для 1-D и MD.КИХ-фильтры более популярны, поскольку их проще реализовать. Для одномерных банков КИХ-фильтров с передискретизацией алгоритм Евклида играет ключевую роль в обратной матричной задаче. Однако алгоритм Евклида не работает для многомерных (MD) фильтров. Для MD-фильтра мы можем преобразовать КИХ-представление в полиномиальное представление. А затем используйте алгебраическую геометрию и базисы Грёбнера, чтобы получить структуру и условия реконструкции многомерных банков фильтров с передискретизацией.

Многомерные банки КИХ-фильтров без субдискретизации

Банки фильтров без субдискретизации — это особые банки фильтров с передискретизацией без понижающей или повышающей дискретизации.Идеальное условие восстановления для банков КИХ-фильтров без субдискретизации приводит к векторной обратной задаче:фильтры анализа $\{H_{1},...,H_{N}\}$ даны и КИХ, и цель состоит в том, чтобы найти набор фильтров КИХ-синтеза. $\{G_{1},...,G_{N}\}$ удовлетворительно.

Использование базисов Грёбнера

Многомерные банки M-канальных фильтров

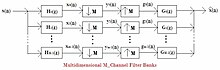
Поскольку многомерные банки фильтров могут быть представлены многомерными рациональными матрицами, этот метод является очень эффективным инструментом, который можно использовать для работы с многомерными банками фильтров.

В Чаро, представлен и обсужден многомерный полиномиальный алгоритм матричной факторизации. Наиболее распространенной проблемой являются многомерные банки фильтров для идеальной реконструкции. В этой статье рассказывается о методе достижения этой цели, который удовлетворяет ограниченному условию линейной фазы.

Согласно описанию статьи, некоторые новые результаты факторизации обсуждаются и применяются к вопросам многомерных банков фильтров с линейной идеальной фазовой реконструкцией и конечной импульсной характеристикой. Основное понятие базисов Грёбнера дано у Адамса.

Этот подход, основанный на многомерной матричной факторизации, может быть использован в разных областях. Алгоритмическая теория полиномиальных идеалов и модулей может быть модифицирована для решения проблем обработки, сжатия, передачи и декодирования многомерных сигналов.

Общий банк многомерных фильтров (рис. 7) может быть представлен парой многофазных матриц анализа и синтеза. $H(z)$ и $G(z)$ размера $N\times M$ и $M\times N$, где N — количество каналов и $M{\stackrel {\rm {def}}{=}}|M|$ – абсолютное значение определителя матрицы выборки. Также $H(z)$ и $G(z)$ представляют собой z-преобразование многофазных компонентов фильтров анализа и синтеза. Следовательно, они представляют собой многомерные полиномы Лорана , имеющие общий вид:

$F(z)=\sum _{k\in \mathbf {Z} ^{d}}f[k]z^{k}=\sum _{k\in \mathbf {Z} ^{d}}f[k_{1},...,k_{d}]z_{1}^{k_{1}}...z_{d}^{k_{d}}$.

Чтобы спроектировать наборы фильтров идеальной реконструкции, необходимо решить полиномиальное матричное уравнение Лорана:

$G(z)H(z)=I_{|M|}$.

В многомерном случае с многомерными полиномами необходимо использовать теорию и алгоритмы базисов Грёбнера.

Базисы Грёбнера можно использовать для характеристики банков многомерных фильтров идеальной реконструкции, но сначала их необходимо расширить от полиномиальных матриц до полиномиальных матриц Лорана.

Вычисление на основе Грёбнера можно эквивалентно рассматривать как метод исключения Гаусса для решения полиномиального матричного уравнения $G(z)H(z)=I_{|M|}$.Если у нас есть набор полиномиальных векторов

$\mathrm {Module} \left\{h_{1}(z),...,h_{N}(z)\right\}{\stackrel {\rm {def}}{=}}\{c_{1}(z)h_{1}(z)+...+c_{N}(z)h_{N}(z)\}$

где $c_{1}(z),...,c_{N}(z)$ являются полиномами.

Модуль аналогичен набору векторов в линейной алгебре. Теория базисов Грёбнера подразумевает, что Модуль имеет единственный приведенный базис Грёбнера для заданного порядка степенных произведений в полиномах.

Если мы определим базис Грёбнера как $\left\{b_{1}(z),...,b_{N}(z)\right\}$, это может бытьполучено от $\left\{h_{1}(z),...,h_{N}(z)\right\}$ конечной последовательностью приведения(деление) шагов.

Используя реверс-инжиниринг, мы можем вычислить базисные векторы $b_{i}(z)$ в терминах исходных векторов $h_{j}(z)$ через $K\times N$ матрица преобразования $W_{ij}(z)$ как:

$b_{i}(z)=\sum _{j=1}^{N}W_{ij}(z)h_{j}(z),i=1,...,K$

Банки многомерных фильтров на основе картографирования

Разработка фильтров с хорошими частотными характеристиками при использовании подхода на основе баз Грёбнера является сложной задачей.
Проектирование на основе картографирования широко используется для разработки неразделимых многомерных банков фильтров с хорошими частотными характеристиками.

Подходы к отображению имеют определенные ограничения на типы фильтров; однако это дает много важных преимуществ, таких как эффективная реализация с помощью подъемно-лестничных конструкций.Здесь мы приводим пример двухканальных банков фильтров в 2D с матрицей выборки.
$D_{1}=\left[{\begin{array}{cc}2&0\\0&1\end{array}}\right]$У нас будет несколько возможных вариантов идеальных частотных характеристик канального фильтра. $H_{0}(\xi )$ и $G_{0}(\xi )$. (Обратите внимание, что два других фильтра $H_{1}(\xi )$ и $G_{1}(\xi )$ поддерживаются в дополнительных регионах.)
Все частотные области на рисунке могут быть критически дискретизированы с помощью прямоугольной решетки, охватывающей $D_{1}$.
Итак, представьте, что набор фильтров достигает идеальной реконструкции.с FIR-фильтрами. Тогда из характеристики многофазной области следует, что фильтры H1(z) и G1(z) полностьюзаданные H0(z) и G0(z) соответственно. Следовательно, нам необходимо спроектировать H0(x) и G0(z), которые имеют желаемые частотные характеристики и удовлетворяют условиям многофазной области. $H_{0}(z_{1},z_{2})G_{0}(z_{1},z_{2})+H_{0}(-z_{1},z_{2})G_{0}(-z_{1},z_{2})=2$
Существуют различные методы сопоставления, которые можно использовать для получения вышеуказанного результата.

Проектирование банка фильтров в частотной области

Когда идеальная реконструкция не требуется, задачу проектирования можно упростить, работая в частотной области вместо использования КИХ-фильтров.
Обратите внимание, что метод частотной области не ограничивается разработкой банков фильтров без субдискретизации (см. ).

Прямая оптимизация в частотной области

Многие из существующих методов проектирования двухканальных наборов фильтров основаны на методе преобразования переменных. Например, преобразование Макклеллана можно использовать для разработки одномерных двухканальных наборов фильтров. Хотя наборы 2D-фильтров имеют много схожих свойств с 1D-прототипом, их трудно распространить на более чем 2-канальные случаи.

В Нгуене, авторы говорят о разработке многомерных банков фильтров путем прямой оптимизации в частотной области. Предлагаемый здесь метод в основном ориентирован на проектирование наборов M-канальных 2D-фильтров. Этот метод является гибким в отношении конфигураций поддержки частоты. Банки 2D-фильтров, разработанные путем оптимизации в частотной области, использовались в Wei. и Лу. В статье Нгуена предлагаемый метод не ограничивается созданием двухканальных наборов 2D-фильтров; подход обобщается на банки M-канальных фильтров с любой критической матрицей субдискретизации. Согласно реализации, описанной в статье, его можно использовать для создания до 8-канальных наборов 2D-фильтров.

(6) Матрица обратной оболочки

В статье Ли 1999 г. авторы говорят о конструкции многомерного банка фильтров с использованием матрицы обратной оболочки . Пусть H — матрица Адамара порядка n , транспонирование H тесно связано с ее обратным. Правильная формула: $HH^{T}=I_{n}$, где I _n — единичная матрица размера n×n, а H ^Т является транспонированием H . В статье 1999 г. авторы обобщают матрицу обратной рубашки [RJ] _N, используя матрицы Адамара и взвешенные матрицы Адамара.

В этой статье авторы предложили использовать КИХ-фильтр со 128 отводами в качестве базового фильтра, а для матриц RJ вычислять коэффициент прореживания. Они выполнили моделирование на основе различных параметров и добились хороших результатов при низком коэффициенте децимации.

Банки направленных фильтров

Бамбергер и Смит предложили набор двумерных направленных фильтров (DFB). DFB эффективно реализуется посредством l -уровневой древовидной декомпозиции, которая приводит к $2^{l}$ поддиапазоны с клиновидным частотным разделением (см. рисунок).Оригинальная конструкция DFB предполагает модуляцию входного сигнала и использование ромбовидных фильтров.Более того, чтобы получить желаемое частотное разбиение, необходимо следовать сложному правилу развертывания дерева. В результате частотные областидля результирующих поддиапазонов не требуется простой порядок, как показано на рисунке 9, на основе индексов каналов.

Первое преимущество DFB заключается в том, что оно не только не является избыточным преобразованием, но и обеспечивает идеальную реконструкцию.Еще одним преимуществом DFB является его направленная избирательность и эффективная структура.Это преимущество делает DFB подходящим подходом для многих применений обработки сигналов и изображений. (например, пирамида Лапласа, построенная контурлетами, представление разреженных изображений, медицинская визуализация, и т. д.).

Банки направленных фильтров могут быть расширены до более высоких размеров. Его можно использовать в 3-D для получения частотного разделения.

Приемопередатчик банка фильтров

Банки фильтров являются важными элементами физического уровня широкополосной беспроводной связи, где проблема заключается в эффективной обработке нескольких каналов в основной полосе частот. Архитектура приемопередатчика на основе банка фильтров устраняет проблемы масштабируемости и эффективности, наблюдавшиеся в предыдущих схемах в случае несмежных каналов. Соответствующая конструкция фильтра необходима для уменьшения снижения производительности, вызванного набором фильтров. Чтобы получить универсально применимые конструкции, можно сделать умеренные предположения о формате сигнала, статистике канала и схеме кодирования/декодирования. Могут использоваться как эвристические, так и оптимальные методологии проектирования, и отличная производительность возможна при низкой сложности, пока трансивер работает с достаточно большим коэффициентом передискретизации. Практическое применение — передача OFDM, где они обеспечивают очень хорошую производительность при небольшой дополнительной сложности.

Ссылки

Дальнейшее чтение

• Харрис, Фредрик Дж. (2004). Многоскоростная обработка сигналов для систем связи . Река Аппер-Сэддл, Нью-Джерси: PTR Prentice Hall. ISBN  0-13-146511-2 .