Пуассоновский вейвлет

В математике, в функциональном анализе, несколько различных вейвлетов известно под названием вейвлет Пуассона . В одном контексте термин «вейвлет Пуассона» используется для обозначения семейства вейвлетов, помеченных набором положительных целых чисел , члены которых связаны с распределением вероятностей Пуассона . Эти вейвлеты были впервые определены и изучены Карлин А. Косанович, Алланом Р. Мозером и Майклом Дж. Пиовосо в 1995–96 годах. ^[1]^[2] В другом контексте этот термин относится к определенному вейвлету, который включает в себя форму интегрального ядра Пуассона. ^[3] В еще одном контексте эта терминология используется для описания семейства комплексных вейвлетов, индексированных положительными целыми числами, которые связаны с производными интегрального ядра Пуассона. ^[4]

Вейвлеты, связанные с распределением вероятностей Пуассона

Определение

Члены семейства пуассоновских вейвлетов, соответствующие n = 1, 2, 3, 4.

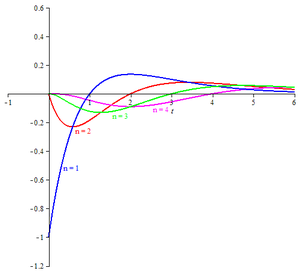
Для каждого положительного целого числа n вейвлет Пуассона $\psi _{n}(t)$ определяется

\psi _{n}(t)={\begin{cases}\left({\frac {t-n}{n!}}\right)t^{n-1}e^{-t}&{\text{ for }}t\geq 0\\0&{\text{ for }}t<0.\end{cases}}

Чтобы увидеть связь между вейвлетом Пуассона и распределением Пуассона, пусть X будет дискретной случайной величиной, имеющей распределение Пуассона с параметром (средним) t , и для каждого неотрицательного целого числа n пусть Prob( X = n ) = p _n ( т ). Тогда у нас есть

p_{n}(t)={\frac {t^{n}}{n!}}e^{-t}.

Пуассоновский вейвлет $\psi _{n}(t)$ теперь дается

\psi _{n}(t)=-{\frac {d}{dt}}p_{n}(t).

Основные свойства

$\psi _{n}(t)$ – обратная разность значений распределения Пуассона:

\psi _{n}(t)=p_{n}(t)-p_{n-1}(t).

«Волнистость» членов этого семейства вейвлетов следует из

\int _{-\infty }^{\infty }\psi _{n}(t)\,dt=0.

Преобразование Фурье $\psi _{n}(t)$ дан

\Psi (\omega )={\frac {-i\omega }{(1+i\omega )^{n+1}}}.

Константа допустимости, связанная с $\psi _{n}(t)$ является

C_{\psi _{n}}=\int _{-\infty }^{\infty }{\frac {\left|\Psi _{n}(\omega )\right|^{2}}{|\omega |}}\,d\omega ={\frac {1}{n}}.

Вейвлет Пуассона не является ортогональным семейством вейвлетов.

Вейвлет-преобразование Пуассона

Семейство вейвлетов Пуассона можно использовать для построения семейства вейвлет-преобразований Пуассона функций, определенных во временной области. Поскольку вейвлеты Пуассона также удовлетворяют условию допустимости, функции во временной области могут быть восстановлены из их вейвлет-преобразований Пуассона, используя формулу для обратных вейвлет-преобразований с непрерывным временем.

Если f ( t ) является функцией во временной области, ее n -е вейвлет-преобразование Пуассона определяется выражением

(W_{n}f)(a,b)={\frac {1}{\sqrt {|a|}}}\int _{-\infty }^{\infty }f(t)\psi _{n}\left({\frac {t-b}{a}}\right)\,dt

В обратном направлении, учитывая n -е вейвлет-преобразование Пуассона $(W_{n}f)(a,b)$ функции f ( t ) во временной области функция f ( t ) может быть восстановлена следующим образом:

f(t)={\frac {1}{C_{\psi _{n}}}}\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }\,\left\{(W_{n}f)(a,b){\frac {1}{\sqrt {|a|}}}\psi _{n}\left({\frac {t-b}{a}}\right)\,\right\}db\right]{\frac {da}{a^{2}}}

Приложения

Вейвлет-преобразования Пуассона применялись в анализе с несколькими разрешениями, идентификации систем и оценке параметров. Они особенно полезны при изучении задач, в которых функции во временной области состоят из линейных комбинаций убывающих экспонент с задержкой по времени.

Вейвлет, связанный с ядром Пуассона

Изображение вейвлета, связанного с ядром Пуассона.

Изображение преобразования Фурье вейвлета, связанного с ядром Пуассона.

Определение

Вейвлет Пуассона определяется функцией ^[3]

\psi (t)={\frac {1}{\pi }}{\frac {1-t^{2}}{(1+t^{2})^{2}}}

Это можно выразить в форме

\psi (t)=P(t)+t{\frac {d}{dt}}P(t)

где

P(t)={\frac {1}{\pi }}{\frac {1}{1+t^{2}}}

.

Связь с ядром Пуассона

Функция $P(t)$ появляется как интегральное ядро при решении некоторой начальной задачи оператора Лапласа .

Это проблема начального значения: при любом $s(x)$ в $L^{p}(\mathbb {R} )$ , найдите гармоническую функцию $\phi (x,y)$ определенный в верхней полуплоскости, удовлетворяющий следующим условиям:

$\int _{-\infty }^{\infty }|\phi (x,y)|^{p}\,dx\leq c<\infty$ , и
$\phi (x,y)\rightarrow s(x)$ как $y\rightarrow 0$ в $L^{p}(\mathbb {R} )$ .

Задача имеет следующее решение: существует ровно одна функция $\phi (x,y)$ удовлетворяющее двум условиям, и оно определяется выражением

\phi (t,y)=P_{y}(t)\star s(t)

где $P_{y}(t)={\frac {1}{y}}P\left({\frac {t}{y}}\right)={\frac {1}{\pi }}{\frac {y}{t^{2}+y^{2}}}$ и где" $\star$ " обозначает операцию свертки . Функция $P_{y}(t)$ – интегральное ядро функции $\phi (x,y)$ . Функция $\phi (x,y)$ является гармоническим продолжением $s(x)$ в верхнюю полуплоскость.

Характеристики

«Волнистость» функции следует из

\int _{-\infty }^{\infty }\psi (t)\,dt=0

.

Преобразование Фурье $\psi (t)$ дается

\Psi (\omega )=|\omega |e^{-|\omega |}

.

Константа допустимости равна

C_{\psi }=\int _{-\infty }^{\infty }{\frac {\left|\Psi (\omega )\right|^{2}}{|\omega |}}\,d\omega =2.

Класс комплексных вейвлетов, связанных с ядром Пуассона.

Графики действительных частей вейвлета Пуассона $\psi _{n}(t)$ для $n=1,2,3,4$ .

Графики мнимых частей вейвлета Пуассона $\psi _{n}(t)$ для $n=1,2,3,4$ .

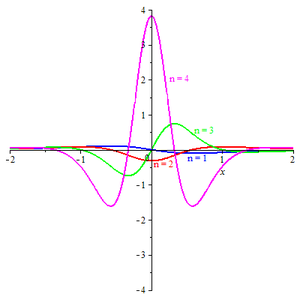
Определение

Вейвлет Пуассона — это семейство комплексных функций, индексированных набором положительных целых чисел и определяемых формулой ^[4]^[5]

\psi _{n}(t)={\frac {1}{2\pi }}(1-it)^{-(n+1)}

где

n=1,2,3,\ldots

Связь с ядром Пуассона

Функция $\psi _{n}(t)$ может быть выражено как n -я производная следующим образом:

\psi _{n}(t)={\frac {1}{2\pi }}{\frac {1}{n!\,i^{n}}}{\frac {d^{n}}{dt^{n}}}\left((1-it)^{-1}\right)

Написание функции $(1-it)^{-1}$ в терминах интегрального ядра Пуассона $P(t)={\frac {1}{1+t^{2}}}$ как

(1-it)^{-1}=P(t)+itP(t)

у нас есть

\psi _{n}(t)={\frac {1}{2\pi }}{\frac {1}{n!\,i^{n}}}{\frac {d^{n}}{dt^{n}}}P(t)+i\left({\frac {1}{2\pi }}{\frac {1}{n!\,i^{n}}}{\frac {d^{n}}{dt^{n}}}\left(tP(t)\right)\right)

Таким образом $\psi _{n}(t)$ можно интерпретировать как функцию, пропорциональную производным интегрального ядра Пуассона.

Характеристики

Преобразование Фурье $\psi _{n}(t)$ дается

\Psi _{n}(\omega )={\frac {1}{\Gamma (n+1)}}\omega ^{n}e^{-\omega }u(\omega )

где $u(\omega )$ — единичная ступенчатая функция .

Ссылки

^ Карлин А. Косанович, Аллан Р. Мозер и Майкл Дж. Пиовосо (1996). «Вейвлет-преобразование Пуассона». Химико-технологические коммуникации . 146 (1): 131–138. дои : 10.1080/00986449608936485 .
^ Карлин А. Косанович, Аллан Р. Мозер и Майкл Дж. Пиовосо (1997). «Новое семейство вейвлетов: вейвлет-преобразование Пуассона». Компьютеры в химической технологии . 21 (6): 601–620. дои : 10.1016/S0098-1354(96)00294-3 .
^ Jump up to: ^а ^б Клес, Роланд; Хаагманс, Роджер, ред. (2000). Вейвлеты в науках о Земле . Берлин: Шпрингер. стр. 18–20.
^ Jump up to: ^а ^б Абдул Дж. Джерри (1998). Феномен Гиббса в анализе Фурье, сплайнах и вейвлет-аппроксимациях . Дордрех: Springer Science+Business Media. стр. 222–224 . ISBN 978-1-4419-4800-7 .
^ Войбор А. Войчинский (1997). Распределения в физических и технических науках: распределительное и фрактальное исчисление, интегральные преобразования и вейвлеты, Том 1 . Springer Science & Business Media. п. 223. ИСБН 9780817639242 .

[def-1] Карлин А. Косанович, Аллан Р. Мозер и Майкл Дж. Пиовосо (1996). «Вейвлет-преобразование Пуассона». Химико-технологические коммуникации . 146 (1): 131–138. дои : 10.1080/00986449608936485 .

[2] Карлин А. Косанович, Аллан Р. Мозер и Майкл Дж. Пиовосо (1997). «Новое семейство вейвлетов: вейвлет-преобразование Пуассона». Компьютеры в химической технологии . 21 (6): 601–620. дои : 10.1016/S0098-1354(96)00294-3 .

[geo-3] Jump up to: ^а ^б Клес, Роланд; Хаагманс, Роджер, ред. (2000). Вейвлеты в науках о Земле . Берлин: Шпрингер. стр. 18–20.

[jerri-4] Jump up to: ^а ^б Абдул Дж. Джерри (1998). Феномен Гиббса в анализе Фурье, сплайнах и вейвлет-аппроксимациях . Дордрех: Springer Science+Business Media. стр. 222–224 . ISBN 978-1-4419-4800-7 .

[5] Войбор А. Войчинский (1997). Распределения в физических и технических науках: распределительное и фрактальное исчисление, интегральные преобразования и вейвлеты, Том 1 . Springer Science & Business Media. п. 223. ИСБН 9780817639242 .

[1]

[2]

[3]

[4]

[5]