ОБЫЧАЙ

Диаграмма КУСУМ
Первоначально предложено	Страница ES
Наблюдения за процессом
Рациональный размер подгруппы	п = 1
Тип измерения	Накопленная сумма качественной характеристики
Тип характеристики качества	Данные переменных
Базовое распределение	Нормальное распределение
Производительность
Размер смещения для обнаружения	≤ 1,5п
Диаграмма изменений процесса
Непригодный
Диаграмма средних значений процесса
Центральная линия	Целевое значение Т качественной характеристики
Верхний контрольный предел	$C_{i}^{+}=\max \lbrack 0,x_{i}-\left(T+K\right)+C_{i-1}^{+}\rbrack$
Нижний предел регулирования	$C_{i}^{-}=\max \lbrack 0,\left(T-K\right)-x_{i}+C_{i-1}^{-}\rbrack$
Построенная статистика	$C_{i}=\sum _{j=1}^{i}{\bar {x}}_{j}-T$

В контроле качества CUSUM статистическом (или контрольная диаграмма совокупной суммы ) представляет собой метод последовательного анализа, разработанный Э.С. Пейджем из Кембриджского университета . Обычно он используется для мониторинга обнаружения изменений . О CUSUM было объявлено в журнале «Биометрика» в 1954 году, через несколько лет после публикации ( Уолда последовательного теста отношения вероятностей SPRT).

ES Пейдж назвал «показатель качества». $\theta$, под которым он имел в виду параметр распределения вероятностей ; например, среднее . Он разработал CUSUM как метод определения изменений в нем и предложил критерий принятия решения о том, когда следует предпринять корректирующие действия. Когда метод CUSUM применяется к изменениям среднего значения, его можно использовать для обнаружения шагов во временном ряду .

Несколько лет спустя Джордж Альфред Барнард разработал метод визуализации — диаграмму V-маски, позволяющую обнаруживать как увеличение, так и уменьшение количества $\theta$.

Метод

Как следует из названия, CUSUM предполагает вычисление совокупной суммы (что и делает ее «последовательной»). Образцы процесса $x_{n}$ присвоены веса $\omega _{n}$и суммируется следующим образом:

$S_{0}=0$

$S_{n+1}=\max(0,S_{n}+x_{n+1}-\omega _{n})$

Когда значение S превышает определенное пороговое значение, обнаружено изменение значения. Приведенная выше формула обнаруживает изменения только в положительном направлении. Когда также необходимо найти отрицательные изменения, вместо операции максимального следует использовать операцию min, и на этот раз изменение было обнаружено, когда значение S ниже ( отрицательного) значения порогового значения.

Пейдж прямо не сказал об этом. $\omega$ представляет собой функцию правдоподобия , но это обычное использование.

Это отличается от SPRT тем, что в качестве нижнего «барьера удержания» всегда используется нулевая функция, а не нижний «барьер удержания». Кроме того, CUSUM не требует использования функции правдоподобия.

В качестве средства оценки эффективности CUSUM Пейдж определил средней длины пробега (ARL) показатель ; «ожидаемое количество статей, выбранных до того, как будут предприняты действия». Далее он написал:

Когда качество продукции удовлетворительное, ARL является мерой затрат, понесенных схемой при ложных срабатываниях, т. е. ошибках первого рода ( Neyman & Pearson , 1936) . ). С другой стороны, при постоянном низком качестве ARL измеряет задержку и, следовательно, количество брака, произведенного до того, как будут предприняты действия по исправлению, т. е. ошибки второго рода .

Пример

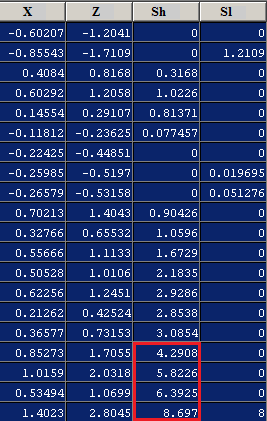
В следующем примере показано 20 наблюдений. $X$ процесса со средним значением 0 и стандартным отклонением 0,5.

Из $Z$ столбец, видно, что $X$ никогда не отклоняется на 3 стандартных отклонения ( $3\sigma$), поэтому простое оповещение о высоком отклонении не приведет к обнаружению сбоя, тогда как CUSUM показывает, что $S_{H}$ значение превышает 4 на 17-м наблюдении.

Столбец	Описание
$X$	Наблюдения за процессом с ожидаемым средним ${\bar {x}}$ 0 и ожидаемое стандартное отклонение $\sigma _{X}$ 0,5
$Z$	Нормализованные наблюдения, т.е. сосредоточенные вокруг среднего значения и масштабированные по стандартному отклонению. $Z_{n}={\frac {X_{n}-{\bar {x}}}{\sigma _{X}}}$
$S_{H}$	Высокое значение CUSUM, обнаруживающее положительную аномалию, ${S_{H}}_{n+1}=\max(0,{S_{H}}_{n}+Z_{n+1}-\omega )$
$S_{L}$	Низкое значение CUSUM , обнаруживающее отрицательную аномалию, ${S_{L}}_{n+1}=\max(0,{S_{L}}_{n}-Z_{n+1}-\omega )$

где $\omega$ — параметр критического уровня (настраиваемый, такой же, как порог T), который используется для настройки чувствительности обнаружения изменений: больше $\omega$ делает CUSUM менее чувствительным к изменениям и наоборот.

Варианты

Совокупные графики наблюдаемых минус ожидаемых являются родственным методом.

Дальнейшее чтение

• Мишель Басвиль и Игорь Никифоров (апрель 1993 г.). Обнаружение резких изменений: теория и применение . Энглвуд Клиффс, Нью-Джерси: Прентис-Холл. ISBN  0-13-126780-9 .
• Мишра С., Ванли О.А. и Парк К. (2015). «Многомерный метод кумулятивной суммы для непрерывного мониторинга повреждений с помощью датчиков волны Лэмба» , Международный журнал прогностики и управления здравоохранением , ISSN   2153-2648

Внешние ссылки

• «Справочник по инженерной статистике - Контрольные диаграммы Cusum»