Обнаружение шагов

Примеры сигналов, которые могут содержать шаги, искаженные шумом. (a) Коэффициенты числа копий ДНК по данным микрочипа , (b) космических лучей интенсивность по данным нейтронного монитора , (c) скорость вращения в зависимости от времени R. Sphaeroides жгутикового двигателя и (d) интенсивность красных пикселей по одной строке сканирования цифровое изображение.

В статистике и обработке сигналов ( обнаружение шага также известное как ступенчатое сглаживание , ступенчатая фильтрация , обнаружение сдвига , обнаружение скачка или обнаружение края ) — это процесс обнаружения резких изменений (шагов, скачков, сдвигов) на среднем уровне временного ряда или сигнал. Обычно его рассматривают как частный случай статистического метода, известного как обнаружение изменений или обнаружение точки изменения. Часто шаг мал, а временной ряд испорчен каким-то шумом , и это усложняет задачу, поскольку шаг может быть скрыт шумом. Поэтому часто требуются алгоритмы статистической обработки и/или обработки сигналов.

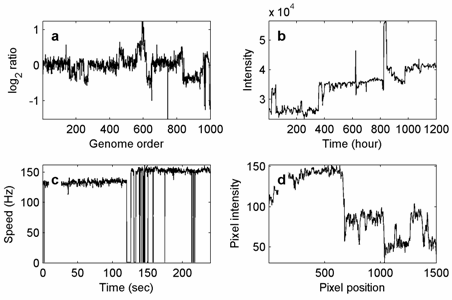
Проблема обнаружения шагов возникает во многих научных и инженерных контекстах, например, при статистическом управлении процессами. ( контрольная карта является наиболее близким методом), в геологоразведочной геофизике (где проблема состоит в том, чтобы разбить данные ГИС на стратиграфические зоны ), в генетике (проблема разделения микрочипов данных числа копий на аналогичные режимы ) и в биофизике (обнаружение переходов состояний в молекулярной машине , записанных во временных координатах ). Для 2D-сигналов соответствующая проблема обнаружения границ интенсивно изучалась при обработке изображений .

Алгоритмы

Когда обнаружение шагов должно выполняться по мере поступления данных, онлайн-алгоритмы . обычно используются и это становится частным случаем последовательного анализа .Такие алгоритмы включают классический метод CUSUM, применяемый к изменениям среднего значения.

Напротив, автономные алгоритмы применяются к данным потенциально спустя долгое время после их получения. Большинство автономных алгоритмов обнаружения шагов в цифровых данных можно разделить на нисходящие , восходящие , скользящие оконные или глобальные методы.

Сверху вниз

Эти алгоритмы начинаются с предположения об отсутствии шагов и по одному вводят возможные шаги-кандидаты, проверяя каждого кандидата, чтобы найти тот, который минимизирует некоторые критерии (например, аппроксимацию оцененного базового кусочно-постоянного сигнала методом наименьших квадратов). Примером может служить алгоритм пошагового размещения прыжков , впервые изученный в геофизических задачах. который нашел недавнее применение в современной биофизике.

Вверх дном

Алгоритмы «снизу вверх» используют «противоположный» подход методам «сверху вниз», сначала предполагая, что между каждой выборкой цифрового сигнала есть шаг, а затем последовательно объединяя шаги на основе некоторых критериев, проверенных для каждого кандидата на слияние.

Раздвижное окно

Рассматривая небольшое «окно» сигнала, эти алгоритмы ищут признаки шага, происходящего внутри окна. Окно «скользит» по временному ряду, шаг за шагом. Доказательства шага проверяются с помощью статистических процедур, например, с использованием двухвыборочного t-критерия Стьюдента . Альтернативно нелинейный фильтр , такой как медианный фильтр к сигналу применяется . Подобные фильтры пытаются удалить шум, сохраняя при этом резкие скачки.

Глобальный

Глобальные алгоритмы рассматривают весь сигнал за один раз и пытаются найти шаги в сигнале с помощью какой-либо процедуры оптимизации. Алгоритмы включают вейвлет -методы, и полное шумоподавление вариаций , в котором используются методы выпуклой оптимизации . Если шаги можно смоделировать как цепь Маркова , то скрытые модели Маркова (популярный подход в биофизическом сообществе). также часто используются ). Когда имеется только несколько уникальных значений среднего, кластеризацию k-средних можно также использовать .

Линейные и нелинейные методы обработки сигналов для обнаружения шагов

Поскольку ступени и (независимый) шум теоретически имеют бесконечную полосу пропускания и, таким образом, перекрываются в базисе Фурье , подходы к обработке сигналов для обнаружения ступенек обычно не используют классические методы сглаживания, такие как фильтр нижних частот . Вместо этого большинство алгоритмов являются явно нелинейными или изменяющимися во времени.

Обнаружение шага и кусочно-постоянные сигналы

Поскольку целью обнаружения шага является обнаружение серии мгновенных скачков среднего значения сигнала, желаемый, основной, средний сигнал является кусочно-постоянным . По этой причине обнаружение шага можно с успехом рассматривать как задачу восстановления кусочно-постоянного сигнала, искаженного шумом. Существуют две взаимодополняющие модели для кусочно-постоянных сигналов: в виде сплайнов с углом 0 градусов с несколькими узлами или в виде наборов уровней с несколькими уникальными уровнями. Поэтому многие алгоритмы обнаружения ступеней лучше всего понимать как методы аппроксимации сплайном 0 градусов или восстановления набора уровней.

Обнаружение шагов как восстановление набора уровней

Когда имеется только несколько уникальных значений среднего значения, такие методы кластеризации, как кластеризация k-средних или сдвиг среднего значения подходят . Эти методы лучше всего понимать как методы поиска описания набора уровней основного кусочно-постоянного сигнала.

Обнаружение ступеньки при подгонке сплайна под углом 0 градусов

Многие алгоритмы явно подгоняют сплайны 0 градусов к зашумленному сигналу, чтобы обнаружить шаги (включая методы пошагового размещения переходов). ), но существуют и другие популярные алгоритмы, которые также можно рассматривать как методы подбора сплайнов после некоторого преобразования, например, полное вариационное шумоподавление .

Обобщенное обнаружение шагов путем кусочно-постоянного шумоподавления

Все упомянутые выше алгоритмы имеют определенные преимущества и недостатки в конкретных обстоятельствах, однако удивительно большое количество этих алгоритмов обнаружения шагов являются частными случаями более общего алгоритма. Этот алгоритм предполагает минимизацию глобального функционала:

$H[m]=\sum _{i=1}^{N}\sum _{j=1}^{N}\Lambda (x_{i}-m_{j},m_{i}-m_{j},x_{i}-x_{j},i-j)$ ( 1 )

Здесь x _i для i = 1,...., N — входной сигнал дискретного времени длины N , а m _i — выходной сигнал алгоритма. Цель состоит в том, чтобы минимизировать H [ m ] относительно выходного сигнала m . Форма функции $\scriptstyle \Lambda$ определяет конкретный алгоритм. Например, выбрав:

$\Lambda ={\frac {1}{2}}\left|x_{i}-m_{j}\right|^{2}I(i-j=0)+\gamma \left|m_{i}-m_{j}\right|I(i-j=1)$

где I ( S ) = 0, если условие S ложно, и другое в противном случае, получает алгоритм общего шумоподавления с параметром регуляризации $\gamma$. Сходным образом:

$\Lambda =\min \left\{{\frac {1}{2}}\left|m_{i}-m_{j}\right|^{2},W\right\}$

приводит к алгоритму среднего сдвига при использовании интегратора Эйлера с адаптивным размером шага, инициализируемого входным сигналом x . Здесь W > 0 — параметр, определяющий поддержку ядра среднего сдвига. Другой пример:

$\Lambda ={\frac {1-\exp(-\beta |m_{i}-m_{j}|^{2}/2)}{\beta }}\cdot I(|i-j|\leq W)$

ведущий к двустороннему фильтру , где $\scriptstyle \beta >0$ — параметр тонального ядра, а W — поддержка пространственного ядра. Еще один частный случай:

$\Lambda ={\frac {1}{2}}\left|x_{i}-m_{j}\right|^{2}I(i-j=0)+\gamma \left|m_{i}-m_{j}\right|^{0}I(i-j=1)$

определение группы алгоритмов, которые пытаются жадно подогнать к сигналу сплайны с нулевой степенью. Здесь, $\scriptstyle \left|x\right|^{0}$ определяется как ноль, если x = 0, и единица в противном случае.

Многие из функционалов в уравнении ( 1 ), определяемые конкретным выбором $\scriptstyle \Lambda$ являются выпуклыми : их можно минимизировать, используя методы выпуклой оптимизации . Третьи невыпуклые, но был разработан ряд алгоритмов минимизации этих функционалов.

Обнаружение шагов с использованием модели Поттса

Классическим вариационным методом обнаружения шагов является модель Поттса. Это задается задачей невыпуклой оптимизации

$u^{*}=\arg \min _{u\in \mathbb {R} ^{N}}\gamma \|\nabla u\|_{0}+\|u-x\|_{p}^{p}$

Термин $\|\nabla u\|_{0}=\#\{i:u_{i}\neq u_{i+1}\}$ наказывается за количество прыжков и срок $\|u-x\|_{p}^{p}=\sum _{i=1}^{N}|u_{i}-x_{i}|^{p}$ измеряет верность данным x . Параметр γ > 0 определяет компромисс между регулярностью и точностью данных . Поскольку минимизатор $u^{*}$ является кусочно-постоянным, шаги задаются ненулевыми положениями градиента $\nabla u^{*}$.Для $p=2$ и $p=1$ существуют быстрые алгоритмы, дающие точное решение задачи Поттса в $O(N^{2})$.

См. также

• Сегментация временных рядов

Внешние ссылки

• PWCTools: гибкое программное обеспечение Matlab и Python для обнаружения ступенек путем кусочно-постоянного шумоподавления.
• Pottslab: набор инструментов Matlab для кусочно-постоянной оценки на основе модели Поттса.