Аналитический сигнал

Не путать с аналитическим выражением или аналитической функцией .

В математике и обработке сигналов аналитический сигнал представляет собой комплексную функцию , не имеющую отрицательных частотных составляющих. Действительная и мнимая части аналитического сигнала представляют собой вещественнозначные функции, связанные друг с другом преобразованием Гильберта .

Аналитическим представлением функции вещественной является аналитический сигнал , содержащий исходную функцию и ее преобразование Гильберта. Такое представление облегчает многие математические манипуляции. Основная идея состоит в том, что отрицательные частотные компоненты преобразования Фурье (или спектра ) вещественнозначной функции излишни из-за эрмитовой симметрии такого спектра. Эти отрицательные частотные компоненты можно отбросить без потери информации, если вместо этого мы готовы иметь дело с комплексной функцией. Это делает определенные атрибуты функции более доступными и облегчает разработку методов модуляции и демодуляции, таких как однополосный.

Пока управляемая функция не имеет отрицательных частотных составляющих (то есть она по-прежнему аналитична ), преобразование из комплексной обратно в действительную является всего лишь вопросом отбрасывания мнимой части. Аналитическое представление является обобщением концепции вектора : в то время как вектор ограничен неизменными во времени амплитудой, фазой и частотой, аналитический сигнал допускает изменяющиеся во времени параметры.

Определение

Передаточная функция для создания аналитического сигнала

Если $s(t)$ это действительная функция с преобразованием Фурье $S(f)$ (где $f$ — действительное значение, обозначающее частоту), то преобразование обладает эрмитовой симметрией относительно $f=0$ ось:

$S(-f)=S(f)^{*},$

где $S(f)^{*}$ представляет собой сопряжение комплексное $S(f)$.Функция:

${\begin{aligned}S_{\mathrm {a} }(f)&\triangleq {\begin{cases}2S(f),&{\text{for}}\ f>0,\\S(f),&{\text{for}}\ f=0,\\0,&{\text{for}}\ f<0\end{cases}}\\&=\underbrace {2\operatorname {u} (f)} _{1+\operatorname {sgn}(f)}S(f)=S(f)+\operatorname {sgn}(f)S(f),\end{aligned}}$

где

• $\operatorname {u} (f)$ – ступенчатая функция Хевисайда ,
• $\operatorname {sgn}(f)$ это знаковая функция ,

содержит только неотрицательные частотные компоненты $S(f)$. И операция обратима в силу эрмитовой симметрии $S(f)$:

${\begin{aligned}S(f)&={\begin{cases}{\frac {1}{2}}S_{\mathrm {a} }(f),&{\text{for}}\ f>0,\\S_{\mathrm {a} }(f),&{\text{for}}\ f=0,\\{\frac {1}{2}}S_{\mathrm {a} }(-f)^{*},&{\text{for}}\ f<0\ {\text{(Hermitian symmetry)}}\end{cases}}\\&={\frac {1}{2}}[S_{\mathrm {a} }(f)+S_{\mathrm {a} }(-f)^{*}].\end{aligned}}$

Аналитический сигнал ​ $s(t)$ — обратное преобразование Фурье $S_{\mathrm {a} }(f)$:

${\begin{aligned}s_{\mathrm {a} }(t)&\triangleq {\mathcal {F}}^{-1}[S_{\mathrm {a} }(f)]\\&={\mathcal {F}}^{-1}[S(f)+\operatorname {sgn}(f)\cdot S(f)]\\&=\underbrace {{\mathcal {F}}^{-1}\{S(f)\}} _{s(t)}+\overbrace {\underbrace {{\mathcal {F}}^{-1}\{\operatorname {sgn}(f)\}} _{j{\frac {1}{\pi t}}}*\underbrace {{\mathcal {F}}^{-1}\{S(f)\}} _{s(t)}} ^{\text{convolution}}\\&=s(t)+j\underbrace {\left[{1 \over \pi t}*s(t)\right]} _{\operatorname {\mathcal {H}} [s(t)]}\\&=s(t)+j{\hat {s}}(t),\end{aligned}}$

где

• ${\hat {s}}(t)\triangleq \operatorname {\mathcal {H}} [s(t)]$ представляет собой Гильберта преобразование $s(t)$;
• $*$ – оператор бинарной свертки ;
• $j$ это мнимая единица .

отмечая, что $s(t)=s(t)*\delta (t),$ это также можно выразить как операцию фильтрации, которая напрямую удаляет отрицательные частотные составляющие :

$s_{\mathrm {a} }(t)=s(t)*\underbrace {\left[\delta (t)+j{1 \over \pi t}\right]} _{{\mathcal {F}}^{-1}\{2u(f)\}}.$

Отрицательные частотные составляющие

С $s(t)=\operatorname {Re} [s_{\mathrm {a} }(t)]$, восстановление отрицательных частотных составляющих — это простой вопрос отбрасывания $\operatorname {Im} [s_{\mathrm {a} }(t)]$ что может показаться нелогичным. Комплексное сопряжение $s_{\mathrm {a} }^{*}(t)$ содержит только отрицательные частотные составляющие. И поэтому $s(t)=\operatorname {Re} [s_{\mathrm {a} }^{*}(t)]$ восстанавливает подавленные положительные частотные составляющие. Другая точка зрения состоит в том, что мнимая компонента в любом случае представляет собой член, который вычитает частотные компоненты из $s(t).$ $\operatorname {Re}$ оператор удаляет вычитание, создавая видимость добавления новых компонентов.

Примеры

Пример 1

$s(t)=\cos(\omega t),$ где $\omega >0.$

Затем:

${\begin{aligned}{\hat {s}}(t)&=\cos \left(\omega t-{\frac {\pi }{2}}\right)=\sin(\omega t),\\s_{\mathrm {a} }(t)&=s(t)+j{\hat {s}}(t)=\cos(\omega t)+j\sin(\omega t)=e^{j\omega t}.\end{aligned}}$

Последнее равенство — это формула Эйлера которой , следствием является ${\textstyle \cos(\omega t)={\frac {1}{2}}\left(e^{j\omega t}+e^{j(-\omega )t}\right).}$ В общем, аналитическое представление простой синусоиды получается путем выражения ее через комплексную экспоненту, отбрасывания отрицательной частотной составляющей и удвоения положительной частотной составляющей. А аналитическое представление суммы синусоид — это сумма аналитических представлений отдельных синусоид.

Пример 2

Здесь мы используем формулу Эйлера для выявления и отбрасывания отрицательной частоты.

$s(t)=\cos(\omega t+\theta )={\frac {1}{2}}\left(e^{j(\omega t+\theta )}+e^{-j(\omega t+\theta )}\right)$

Затем:

$s_{\mathrm {a} }(t)={\begin{cases}e^{j(\omega t+\theta )}\ \ =\ e^{j|\omega |t}\cdot e^{j\theta },&{\text{if}}\ \omega >0,\\e^{-j(\omega t+\theta )}=\ e^{j|\omega |t}\cdot e^{-j\theta },&{\text{if}}\ \omega <0.\end{cases}}$

Пример 3

Это еще один пример использования метода преобразования Гильберта для удаления отрицательных частотных составляющих. Ничто не мешает нам заниматься вычислениями $s_{\mathrm {a} }(t)$ для комплексного значения $s(t)$. Но это может быть необратимое представление, поскольку исходный спектр вообще не симметричен. Таким образом, за исключением этого примера, общее обсуждение предполагает реальные значения. $s(t)$.

$s(t)=e^{-j\omega t}$, где $\omega >0$.

Затем:

${\begin{aligned}{\hat {s}}(t)&=je^{-j\omega t},\\s_{\mathrm {a} }(t)&=e^{-j\omega t}+j^{2}e^{-j\omega t}=e^{-j\omega t}-e^{-j\omega t}=0.\end{aligned}}$

Свойства

Мгновенная амплитуда и фаза

Функция выделена синим цветом, а величина ее аналитического представления красным, что показывает эффект огибающей.

Аналитический сигнал также может быть выражен в полярных координатах :

$s_{\mathrm {a} }(t)=s_{\mathrm {m} }(t)e^{j\phi (t)},$

где введены следующие изменяющиеся во времени величины:

• $s_{\mathrm {m} }(t)\triangleq |s_{\mathrm {a} }(t)|$ называется мгновенной амплитудой или огибающей ;
• $\phi (t)\triangleq \arg \!\left[s_{\mathrm {a} }(t)\right]$ называется мгновенной фазой или фазовым углом .

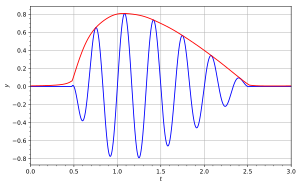
На прилагаемой диаграмме синяя кривая изображает $s(t)$ а красная кривая изображает соответствующий $s_{\mathrm {m} }(t)$.

Производная по времени развернутой мгновенной фазы имеет единицы радиан/секунду и называется мгновенной угловой частотой :

$\omega (t)\triangleq {\frac {d\phi }{dt}}(t).$

( Таким образом, мгновенная частота в герцах ) равна:

$f(t)\triangleq {\frac {1}{2\pi }}\omega (t).$  

Мгновенная амплитуда, мгновенная фаза и частота в некоторых приложениях используются для измерения и обнаружения локальных особенностей сигнала. Другое применение аналитического представления сигнала связано с демодуляцией модулированных сигналов . Полярные координаты удобно разделяют эффекты амплитудной модуляции и фазовой (или частотной) модуляции и эффективно демодулируют определенные виды сигналов.

Сложный конверт/модуль

Аналитические сигналы часто смещаются по частоте (преобразуются с понижением частоты) в сторону 0 Гц, что может создавать [несимметричные] отрицательные частотные компоненты:

$${s_{\mathrm {a} }}_{\downarrow }(t)\triangleq s_{\mathrm {a} }(t)e^{-j\omega _{0}t}=s_{\mathrm {m} }(t)e^{j(\phi (t)-\omega _{0}t)},$$

где $\omega _{0}$ — произвольная опорная угловая частота.

Эта функция имеет разные названия, например, комплексная огибающая и комплексная полоса частот . Сложная оболочка не уникальна; это определяется выбором $\omega _{0}$. Эта концепция часто используется при работе с сигналами полосы пропускания . Если $s(t)$ представляет собой модулированный сигнал, $\omega _{0}$ может быть приравнена к его несущей частоте .

В других случаях $\omega _{0}$ выбирается где-то посередине желаемой полосы пропускания. Затем простой фильтр нижних частот с реальными коэффициентами может исключить интересующую часть. Другой мотив — уменьшить самую высокую частоту, что снижает минимальную частоту выборки без псевдонимов. Сдвиг частоты не подрывает математическую управляемость представления сложного сигнала. Таким образом, в этом смысле преобразованный с понижением частоты сигнал по-прежнему является аналитическим . Однако восстановление вещественного представления уже не является простым вопросом простого извлечения вещественного компонента. Может потребоваться повышающее преобразование, а если сигнал был дискретизирован (дискретное время), интерполяция ( повышающая дискретизация также может потребоваться ), чтобы избежать наложения спектров .

Если $\omega _{0}$ выбирается большей, чем самая высокая частота $s_{\mathrm {a} }(t),$ затем ${s_{\mathrm {a} }}_{\downarrow }(t)$ не имеет положительных частот. В этом случае извлечение реального компонента восстанавливает их, но в обратном порядке; низкочастотные составляющие теперь становятся высокими, и наоборот. Это можно использовать для демодуляции типа однополосного сигнала, называемого нижней боковой полосой или инвертированной боковой полосой .

Иногда рассматриваются другие варианты опорной частоты:

• Иногда $\omega _{0}$ выбран для минимизации
  $$\int _{0}^{+\infty }(\omega -\omega _{0})^{2}|S_{\mathrm {a} }(\omega )|^{2}\,d\omega .$$
• Альтернативно, $\omega _{0}$ может быть выбран так, чтобы минимизировать среднеквадратическую ошибку при линейной аппроксимации развернутой мгновенной фазы $\phi (t)$:
  $$\int _{-\infty }^{+\infty }[\omega (t)-\omega _{0}]^{2}|s_{\mathrm {a} }(t)|^{2}\,dt$$
• или другая альтернатива (для некоторого оптимального $\theta$):
  $$\int _{-\infty }^{+\infty }[\phi (t)-(\omega _{0}t+\theta )]^{2}\,dt.$$

В области частотно-временной обработки сигналов было показано, что аналитический сигнал необходим для определения распределения Вигнера – Вилля , чтобы метод мог иметь желаемые свойства, необходимые для практического применения.

Иногда фразе «комплексная огибающая» придают более простое значение комплексной амплитуды вектора (постоянной частоты); в других случаях сложный конверт $s_{m}(t)$ как определено выше, интерпретируется как зависящее от времени обобщение комплексной амплитуды. Их соотношение мало чем отличается от действительного случая: изменяющаяся огибающая обобщает постоянную амплитуду .

аналитического сигнала на сигналы

Концепция аналитического сигнала четко определена для сигналов одной переменной, которой обычно является время. Для сигналов двух и более переменных аналитический сигнал может быть определен по-разному, и ниже представлены два подхода.

Многомерный аналитический сигнал, основанный на специальном направлении

Прямое обобщение аналитического сигнала можно сделать для многомерного сигнала, как только будет установлено, что подразумевается под отрицательными частотами в этом случае . Это можно сделать, введя единичный вектор ${\boldsymbol {\hat {u}}}$ в области Фурье и обозначьте любой вектор частоты ${\boldsymbol {\xi }}$ как отрицательный, если ${\boldsymbol {\xi }}\cdot {\boldsymbol {\hat {u}}}<0$. Затем аналитический сигнал создается путем удаления всех отрицательных частот и умножения результата на 2 в соответствии с процедурой, описанной для случая сигналов с одной переменной. Однако конкретного направления нет. ${\boldsymbol {\hat {u}}}$ который должен быть выбран, если нет каких-либо дополнительных ограничений. Поэтому выбор ${\boldsymbol {\hat {u}}}$ носит специальный характер или зависит от приложения.

Моногенный сигнал

Действительная и мнимая части аналитического сигнала соответствуют двум элементам моногенного сигнала с векторным знаком , как это определено для сигналов с одной переменной. Однако моногенный сигнал можно напрямую расширить до произвольного числа переменных, создав ( n + 1) -мерную векторную функцию для случая сигналов с n -переменными.

См. также

• Практические соображения по вычислению преобразований Гильберта
• I/Q-данные
• Отрицательная частота

Приложения

• Однополосная модуляция
• Квадратурный фильтр
• Причинный фильтр

Дальнейшее чтение

• Леон Коэн, Частотно-временной анализ , Прентис-Холл, Аппер-Седл-Ривер, 1995.
• Фредерик В. Кинг, Преобразования Гильберта , том. II, Издательство Кембриджского университета, Кембридж, 2009.
• Б. Боашаш, Частотно-временной анализ и обработка сигналов: полный справочник , Elsevier Science, Оксфорд, 2003.

Внешние ссылки

• Аналитические сигналы и фильтры преобразования Гильберта