Группа Коксетера
В математике группа Кокстера , названная в честь HSM Coxeter , представляет собой абстрактную группу , допускающую формальное описание в терминах отражений (или калейдоскопических зеркал ). Действительно, конечные группы Кокстера являются в точности конечными евклидовыми группами отражений ; например, группа симметрии каждого правильного многогранника является конечной группой Кокстера. Однако не все группы Кокстера конечны, и не все можно описать в терминах симметрии и евклидовых отражений. Группы Кокстера были введены в 1934 году как абстракции групп отражения. [1] и конечные группы Кокстера были классифицированы в 1935 году. [2]
Группы Кокстера находят применение во многих областях математики. Примеры конечных групп Кокстера включают группы симметрии правильных многогранников и группы Вейля простых алгебр Ли . Примеры бесконечных групп Кокстера включают группы треугольников, соответствующие регулярным мозаикам евклидовой плоскости и гиперболической плоскости , а также группы Вейля бесконечномерных алгебр Каца – Муди . [3] [4] [5]
Определение [ править ]
Формально группу Кокстера можно определить как группу с представлением
где и является либо целым числом, либо для .Здесь условие означает, что никакое отношение вида для любого целого числа должно быть наложено.
Пара где является группой Кокстера с образующими называется системой Кокстера . Обратите внимание, что в целом не однозначно определяется . Например, группы Кокстера типа и изоморфны, но системы Кокстера не эквивалентны, поскольку первая имеет 3 образующих, а вторая — 1 + 3 = 4 образующих (пояснения к этим обозначениям см. ниже).
Из приведенного выше определения можно сразу сделать ряд выводов.
- Отношение означает, что для всех ; как таковые генераторы являются инволюциями .
- Если , то генераторы и добираться. Это следует из наблюдения, что
- ,
- вместе с
- подразумевает, что
- .
- Альтернативно, поскольку образующие являются инволюциями, , так . есть коммутатор То и равно 1 или, что то же самое, что и добираться.
Причина того, что для в определении предусмотрено, что
- ,
вместе с
уже подразумевает, что
- .
Альтернативным доказательством этого вывода является наблюдение, что и являются сопряженными : действительно .
и Шлефли матрица Матрица Коксетера
Матрица Кокстера – это симметричная матрица с элементами . Действительно, каждая симметричная матрица с диагональными элементами исключительно 1 и недиагональными элементами множества является матрицей Кокстера.
Матрицу Кокстера можно удобно закодировать диаграммой Кокстера согласно следующим правилам.
- Вершины графа помечены индексами генератора.
- Вершины и смежны тогда и только тогда, когда .
- Ребро помечено значением всякий раз, когда значение или больше.
В частности, два генератора коммутируют тогда и только тогда, когда они не соединены ребром. Более того, если граф Кокстера имеет два или более связных компонента , связанная группа является прямым продуктом групп, связанных с отдельными компонентами.Таким образом, дизъюнктное объединение графов Кокстера дает прямое произведение групп Кокстера.
Матрица Кокстера, , связано с Матрица Шлефли с записями , но элементы изменяются, будучи пропорциональными скалярному произведению попарных генераторов. Матрица Шлефли полезна, поскольку ее собственные значения определяют, имеет ли группа Коксетера конечный тип (все положительные), аффинный тип (все неотрицательные, хотя бы один ноль) или неопределенный тип (в противном случае). Неопределенный тип иногда подразделяется, например, на гиперболическую и другие группы Кокстера. Однако существует несколько неэквивалентных определений гиперболических групп Кокстера.
| Группа Коксетера | A 1 ×A 1 | AА2 | BБ2 | Ч 2 | Г 2 | AА3 | BБ3 | Д 4 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Диаграмма Кокстера | ||||||||||
| Матрица Кокстера | ||||||||||
| Матрица Шлефли |
Пример [ править ]
Граф An , в котором вершины с 1 по n расположены в ряд, причем каждая вершина соединена непомеченным ребром со своими непосредственными соседями, представляет собой диаграмму Кокстера симметричной группы Sn 1 + ; образующие (1 2), (2 3 соответствуют транспозициям ), ... , ( n n +1). Любые две непоследовательные транспозиции коммутируют, а умножение двух последовательных транспозиций дает 3-цикл: ( k k +1) ( k +1 k +2) = ( k k +2 k +1). Следовательно, S n+1 является фактором группы Кокстера, имеющей диаграмму An Кокстера . Дальнейшие рассуждения показывают, что это факторотображение является изоморфизмом.
Абстракция групп отражений [ править ]
Группы Кокстера представляют собой абстракцию групп отражения. Группы Кокстера — это абстрактные группы в том смысле, что они задаются посредством представления. С другой стороны, группы отражений конкретны в том смысле, что каждый из ее элементов представляет собой совокупность конечного числа геометрических отражений о линейных гиперплоскостях в некотором евклидовом пространстве. Технически группа отражений — это подгруппа линейной группы (или различных обобщений), порожденная ортогональными матрицами определителя -1. Каждый генератор группы Кокстера имеет порядок 2, что абстрагирует тот геометрический факт, что двукратное отражение является тождественным. Каждое отношение вида , что соответствует геометрическому факту, что для данных двух гиперплоскостей, встречающихся под углом , совокупность двух отражений относительно этих гиперплоскостей представляет собой вращение на , который имеет порядок k .
Таким образом, каждая группа отражений может быть представлена как группа Кокстера. [1] Обратное частично верно: каждая конечная группа Кокстера допускает точное представление как конечная группа отражений некоторого евклидова пространства. [2] Однако не каждая бесконечная группа Кокстера допускает представление в виде группы отражений.
Классифицированы конечные группы Кокстера. [2]
Конечные группы Кокстера [ править ]

Классификация [ править ]
Конечные группы Кокстера классифицируются на основе их диаграмм Кокстера . [2]
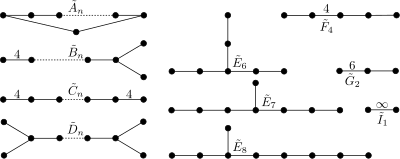
Конечные группы Кокстера со связными диаграммами Кокстера состоят из трех однопараметрических семейств возрастающего ранга. однопараметрическое семейство размерности два, и 6 исключительных групп: и . Каждая конечная группа Кокстера является прямым произведением конечного числа групп Кокстера из приведенного выше списка.
Группы Вейля [ править ]
Многие из них, но не все, являются группами Вейля, и каждую группу Вейля можно реализовать как группу Кокстера. Группы Вейля – это семейства и и исключения и обозначается в обозначениях группы Вейля как
Не-Вейлевские являются исключением. и и те члены семьи которые не являются исключительно изоморфными группе Вейля (а именно и ).
Это можно доказать, сравнив ограничения на (неориентированные) диаграммы Дынкина с ограничениями на диаграммы Кокстера конечных групп: формально граф Кокстера можно получить из диаграммы Дынкина, отбросив направление ребер и заменив каждое двойное ребро на ребро с меткой 4 и каждое тройное ребро с ребром с меткой 6. Также обратите внимание, что каждая конечно порожденная группа Кокстера является автоматической группой . [6] Диаграммы Дынкина имеют дополнительное ограничение: разрешены только метки ребер 2, 3, 4 и 6, что дает вышеизложенное. Геометрически это соответствует кристаллографической ограничительной теореме и тому факту, что исключенные многогранники не заполняют пространство и не мозаично закрывают плоскость – для додекаэдр (двойственно икосаэдр) не заполняет пространство; для 120-ячеечный (дважды 600-ячеечный) не заполняет пространство; для p исключением -угольник не замостит плоскость, за или (треугольные, квадратные и шестиугольные мозаики соответственно).
Обратите внимание далее, что (ориентированные) диаграммы Дынкина B n и C n порождают одну и ту же группу Вейля (следовательно, группу Коксетера), поскольку они различаются как ориентированные графы, но согласуются как неориентированные графы - направление имеет значение для корневых систем, но не для системы Вейля. группа; это соответствует тому, что гиперкуб и кросс-многогранник являются разными правильными многогранниками, но имеют одну и ту же группу симметрии.
Свойства [ править ]
Некоторые свойства конечных неприводимых групп Кокстера приведены в следующей таблице. Порядок приводимой группы можно вычислить как произведение порядков ее неприводимых подгрупп.
| Классифицировать н | Группа символ | Альтернативный символ | Кронштейн обозначение | Коксетер график | Размышления м = 1 ⁄ 2 nh [7] | Номер Кокстера час | Заказ | Структура группы [8] | Связанные многогранники |
|---|---|---|---|---|---|---|---|---|---|
| 1 | А 1 | А 1 | [ ] | 1 | 2 | 2 | { } | ||
| 2 | AА2 | AА2 | [3] | 3 | 3 | 6 | {3} | ||
| 3 | AА3 | AА3 | [3,3] | 6 | 4 | 24 | {3,3} | ||
| 4 | A 4 | A 4 | [3,3,3] | 10 | 5 | 120 | {3,3,3} | ||
| 5 | AА5 | AА5 | [3,3,3,3] | 15 | 6 | 720 | {3,3,3,3} | ||
| н | н | н | [3 п -1 ] | п ( п + 1)/2 | п + 1 | ( п + 1)! | n -симплекс | ||
| 2 | BБ2 | С 2 | [4] | 4 | 4 | 8 | {4} | ||
| 3 | BБ3 | С 3 | [4,3] | 9 | 6 | 48 | {4,3} / {3,4} | ||
| 4 | Б 4 | С 4 | [4,3,3] | 16 | 8 | 384 | {4,3,3} / {3,3,4} | ||
| 5 | Б 5 | С 5 | [4,3,3,3] | 25 | 10 | 3840 | {4,3,3,3} / {3,3,3,4} | ||
| н | Б н | С н | [4,3 п -2 ] | н 2 | 2 н | 2 н н ! | n -куб/ n- ортоплекс | ||
| 4 | Д 4 | Б 4 | [3 1,1,1 ] | 12 | 6 | 192 | ч{4,3,3} / {3,3 1,1 } | ||
| 5 | Д 5 | Б 5 | [3 2,1,1 ] | 20 | 8 | 1920 | ч{4,3,3,3} / {3,3,3 1,1 } | ||
| н | Д н | Б н | [3 п -3,1,1 ] | п ( п - 1) | 2( п - 1) | 2 п -1 н ! | н -демикуб / н -ортоплекс | ||
| 6 | EЕ6 | EЕ6 | [3 2,2,1 ] | 36 | 12 | 51840 (72х6!) | |||
| 7 | E 7 | E 7 | [3 3,2,1 ] | 63 | 18 | 2903040 (72х8!) | 3 21 , 2 31 , 1 32 | ||
| 8 | E8 | E8 | [3 4,2,1 ] | 120 | 30 | 696729600 (192х10!) | 4 21 , 2 41 , 1 42 | ||
| 4 | FF4 | FF4 | [3,4,3] | 24 | 12 | 1152 | {3,4,3} | ||
| 2 | Г 2 | – ( Д 6 2 ) | [6] | 6 | 6 | 12 | {6} | ||
| 2 | Ч 2 | Г 2 | [5] | 5 | 5 | 10 | {5} | ||
| 3 | HH3 | Г 3 | [3,5] | 15 | 10 | 120 | {3,5} / {5,3} | ||
| 4 | Ч 4 | Г 4 | [3,3,5] | 60 | 30 | 14400 | [а] | {5,3,3} / {3,3,5} | |
| 2 | я 2 ( н ) | Д н 2 | [ н ] | н | н | 2 н | когда п = р к + 1, п простое когда п = р к − 1, п простое | { п } |
Группы симметрии правильных многогранников [ править ]
Группа симметрии любого правильного многогранника является конечной группой Кокстера. Обратите внимание, что двойственные многогранники имеют одну и ту же группу симметрии.
Существует три серии правильных многогранников во всех измерениях. Группой симметрии регулярного n -симплекса является симметрическая группа Sn + 1 известная как группа Кокстера типа An , также . Группа симметрии n - куба и его двойственного n -кросс-многогранника равна Bn и известна как гипероктаэдрическая группа .
Исключительные правильные многогранники размерностей два, три и четыре соответствуют другим группам Кокстера. В двух измерениях группы диэдра , которые являются группами симметрии правильных многоугольников , образуют ряд I 2 ( p ) для p ≥ 3. В трех измерениях группа симметрии правильного додекаэдра и его двойственного, правильного икосаэдра , является H 3 , известная как полная группа икосаэдра . В четырех измерениях существуют три исключительных правильных многогранника: 24-ячеечный , 120-ячеечный и 600-ячеечный . Первый имеет группу симметрии F 4 , а два других двойственны и имеют группу симметрии H 4 .
типа Dn , , E6 и . E7 являются группами Группы Кокстера E8 многогранников некоторых полуправильных симметрии
| Таблица семейств неприводимых многогранников | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Семья н | n - симплекс | n - гиперкуб | n - ортоплекс | n - демикуб | 1 к2 | 2 к1 | до 21 числа | пятиугольный многогранник | ||||||||
| Группа | н | Б н |
|
| Ч н | |||||||||||
| 2 |  |  |  п-гон (пример: p=7 ) |  Шестиугольник |  Пентагон | |||||||||||
| 3 |  Тетраэдр | 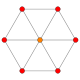 Куб | 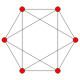 Октаэдр |  Тетраэдр |  Додекаэдр |  Икосаэдр | ||||||||||
| 4 |  5-клеточный |  |  16-ячеечный |  |  24-ячеечный |  120-ячеечный |  600-ячеечный | |||||||||
| 5 |  5-симплекс |  5-куб |  5-ортоплекс |  5-демикуб | ||||||||||||
| 6 |  6-симплекс |  6-куб. |  6-ортоплекс |  6-демикуб |  1 22 |  2 21 | ||||||||||
| 7 |  7-симплекс |  7-куб |  7-ортоплекс |  7-демикуб |  1 32 |  2 31 |  3 21 | |||||||||
| 8 |  8-симплекс |  8-кубовый |  8-ортоплекс |  8-демикуб |  1 42 |  2 41 |  4 21 | |||||||||
| 9 |  9-симплекс |  9-куб |  9-ортоплекс |  9-демикуб | ||||||||||||
| 10 |  10-симплекс |  10-кубовый |  10-ортоплекс |  10-демикуб | ||||||||||||
Аффинные группы Кокстера [ править ]

Аффинные группы Кокстера образуют вторую важную серию групп Кокстера. Они сами по себе не конечны, но каждая содержит нормальную абелеву подгруппу, такую что соответствующая факторгруппа конечна. В каждом случае факторгруппа сама является группой Кокстера, а граф Кокстера аффинной группы Кокстера получается из графа Кокстера факторгруппы путем добавления еще одной вершины и одного или двух дополнительных ребер. Например, при n ≥ 2 граф, состоящий из +1 вершин в окружности, получается из An An таким образом, а соответствующая группа Кокстера является аффинной группой Вейля ( n аффинная симметрическая группа ). При n = 2 это можно представить как подгруппу группы симметрии стандартного замощения плоскости равносторонними треугольниками.
В общем, учитывая корневую систему, можно построить соответствующую Стифеля диаграмму , состоящую из гиперплоскостей, ортогональных корням, а также определенных сдвигов этих гиперплоскостей. Аффинная группа Коксетера (или аффинная группа Вейля) — это группа, порожденная (аффинными) отражениями обо всех гиперплоскостях на диаграмме. [9] Диаграмма Штифеля делит плоскость на бесконечное число компонент связности, называемых альковами , и аффинная группа Коксетера действует свободно и транзитивно на альковах, так же, как обычная группа Вейля действует свободно и транзитивно на камерах Вейля. На рисунке справа показана диаграмма Штифеля для корневая система.
Предполагать является неприводимой корневой системой ранга и пусть быть совокупностью простых корней. Пусть также, обозначают высший корень. Тогда аффинная группа Кокстера порождается обычными (линейными) отражениями относительно гиперплоскостей, перпендикулярных , вместе с аффинным отражением о сдвиге гиперплоскости, перпендикулярной . Граф Кокстера для аффинной группы Вейля представляет собой диаграмму Кокстера – Дынкина для , вместе с одним дополнительным узлом, связанным с . В этом случае одну нишу диаграммы Штифеля можно получить, взяв фундаментальную камеру Вейля и разрезав ее сдвигом гиперплоскости, перпендикулярной . [10]
Список аффинных групп Кокстера следующий:
| Группа символ | Витт символ | Обозначение в скобках | Коксетер график | Связанная однородная тесселяция |
|---|---|---|---|---|
| [3 [ н ] ] | или | Симплектические соты | ||
| [4,3 п - 3 ,3 1,1 ] | Демигиперкубические соты | |||
| [4,3 п -2 ,4] | Гиперкубические соты | |||
| [ 3 1,1 ,3 п -4 ,3 1,1 ] | Демигиперкубические соты | |||
| [3 2,2,2 ] | 2 22 | |||
| [3 3,3,1 ] | 3 31 , 1 33 | |||
| [3 5,2,1 ] | 5 21 , 2 51 , 1 52 | |||
| [3,4,3,3] | 16-ячеечная сотовая связь 24-ячеистые соты | |||
| [6,3] | Шестиугольная плитка и Треугольная плитка | |||
| [∞] | Апейрогон |
Индекс символа группы в каждом случае на единицу меньше количества узлов, поскольку каждая из этих групп была получена путем добавления узла в граф конечной группы.
Кокстера Гиперболические группы
Существует бесконечно много гиперболических групп Кокстера, описывающих группы отражений в гиперболическом пространстве , в том числе гиперболические группы треугольников.
Неприводимые группы Кокстера [ править ]
Группа Кокстера называется неприводимой , если ее диаграмма Кокстера–Дынкина связна. Каждая группа Кокстера является прямым произведением неприводимых групп, соответствующих компонентам ее диаграммы Кокстера – Дынкина.
Частичные заказы [ править ]
Выбор генераторов отражения приводит к возникновению функции длины ℓ в группе Кокстера, а именно минимального количества использований генераторов, необходимых для выражения элемента группы; это именно длина слова метрики в графе Кэли . Выражение для v с использованием генераторов ℓ ( v ) представляет собой сокращенное слово . Например, перестановка (13) в S 3 имеет два сокращенных слова: (12)(23)(12) и (23)(12)(23). Функция определяет карту обобщающее отображение знаков для симметричной группы.
Используя сокращенные слова, можно определить три частичных порядка в группе Коксетера: (правый) слабый порядок , абсолютный порядок и порядок Брюа (названный в честь Франсуа Брюа ). Элемент v превышает элемент u в порядке Брюа, если какое-то (или, что то же самое, любое) сокращенное слово для v содержит сокращенное слово для u в виде подстроки, в которой некоторые буквы (в любой позиции) опущены. В слабом порядке v ≥ u , если некоторое приведенное слово для v содержит приведенное слово для u в качестве начального сегмента. Действительно, длина слова превращает это в градуированное частичное множество . Диаграммы Хассе , соответствующие этим порядкам, являются объектами исследования и связаны с графом Кэли, определяемым генераторами. Абсолютный порядок определяется аналогично слабому порядку, но с порождающим набором/алфавитом, состоящим из всех сопряженных генераторов Кокстера.
Например, перестановка (1 2 3) в S 3 имеет только одно сокращенное слово, (12)(23), поэтому покрывает (12) и (23) в порядке Брюа, но покрывает только (12) в слабом порядке.
Гомология [ править ]
Поскольку группа Кокстера порождается конечным числом элементов порядка 2, ее абелианизация представляет собой элементарную абелеву 2-группу , т. е. изоморфна прямой сумме нескольких копий циклической группы . Это можно переформулировать в терминах первой гомологии группы .
Шура Множитель , равный второй группе гомологий , было вычислено в ( Ihara & Yokonuma 1965 ) для конечных групп отражений и в ( Yokonuma 1965 ) для аффинных групп отражений, с более унифицированным описанием, данным в ( Howlett 1988 ). Во всех случаях мультипликатор Шура также является элементарной абелевой 2-группой. Для каждой бесконечной семьи конечных или аффинных групп Вейля, ранг стабилизируется как уходит в бесконечность.
См. также [ править ]
- Группа Артина-Титса
- Теорема Шевалле – Шепарда – Тодда
- Комплексная группа отражений
- Элемент Кокстера
- Алгебра Ивахори–Хекке , квантовая деформация групповой алгебры
- Kazhdan–Lusztig polynomial
- Самый длинный элемент группы Кокстера
- Параболическая подгруппа группы отражений
- Сверхразрешимая договоренность
Примечания [ править ]
- ^ подгруппа индекса 2
Ссылки [ править ]
- ^ Jump up to: Перейти обратно: а б Коксетер, HSM (1934). «Дискретные группы, порожденные отражениями». Анналы математики . 35 (3): 588–621. CiteSeerX 10.1.1.128.471 . дои : 10.2307/1968753 . JSTOR 1968753 .
- ^ Jump up to: Перейти обратно: а б с д Коксетер, HSM (январь 1935 г.). «Полное перечисление конечных групп вида ". Журнал Лондонского математического общества : 21–25. doi : 10.1112/jlms/s1-10.37.21 .
- ^ Бурбаки, Николя (2002). «4-6». Группы Ли и алгебры Ли . Элементы математики. Спрингер. ISBN 978-3-540-42650-9 . Збл 0983.17001 .
- ^ Хамфрис, Джеймс Э. (1990). Группы отражения и группы Кокстера (PDF) . Кембриджские исследования по высшей математике. Том. 29. Издательство Кембриджского университета. дои : 10.1017/CBO9780511623646 . ISBN 978-0-521-43613-7 . Збл 0725.20028 . Проверено 18 ноября 2023 г.
- ^ Дэвис, Майкл В. (2007). Геометрия и топология групп Кокстера (PDF) . Издательство Принстонского университета. ISBN 978-0-691-13138-2 . Збл 1142.20020 . Проверено 18 ноября 2023 г.
- ^ Бринк, Бриджит; Хоулетт, Роберт Б. (1993). «Свойство конечности и автоматическая структура групп Кокстера». Математические Аннален . 296 (1): 179–190. дои : 10.1007/BF01445101 . S2CID 122177473 . Збл 0793.20036 .
- ^ Коксетер, HSM (январь 1973 г.). «12.6. Число отражений». Правильные многогранники . Курьерская корпорация. ISBN 0-486-61480-8 .
- ^ Уилсон, Роберт А. (2009), «Глава 2», Конечные простые группы , Тексты для аспирантов по математике 251, том. 251, Берлин, Нью-Йорк: Springer-Verlag , номер номера : 10.1007/978-1-84800-988-2 , ISBN. 978-1-84800-987-5
- ^ Зал 2015 г., раздел 13.6.
- ↑ Hall 2015. Глава 13, упражнения 12 и 13.
Библиография [ править ]
- Холл, Брайан С. (2015). Группы Ли, алгебры Ли и представления: элементарное введение . Тексты для аспирантов по математике. Том. 222 (2-е изд.). Спрингер. ISBN 978-3-319-13466-6 .
- Ихара, С.; Ёконума, Такео (1965). «О вторых группах когомологий (мультипликаторах Шура) конечных групп отражений» (PDF) . Дж. Фак. наук. унив. Токио, разд. 1 . 11 : 155–171. Збл 0136.28802 . Архивировано из оригинала (PDF) 23 октября 2013 г.
- Хоулетт, Роберт Б. (1988). «О множителях Шура групп Кокстера». Дж. Лондон Математика. Соц . 2. 38 (2): 263–276. дои : 10.1112/jlms/s2-38.2.263 . Збл 0627.20019 .
- Ёконума, Такео (1965). «О вторых группах когомологий (мультипликаторах Шура) бесконечных дискретных групп отражений». Дж. Фак. наук. унив. Токио, разд. 1 . 11 : 173–186. hdl : 2261/6049 . Збл 0136.28803 .
Дальнейшее чтение [ править ]
- Бьёрнер, Андерс ; Бренти, Франческо (2005). Комбинаторика групп Кокстера . Тексты для аспирантов по математике . Том. 231. Спрингер. ISBN 978-3-540-27596-1 . Збл 1110.05001 .
- Гроув, Ларри К.; Бенсон, Кларк Т. (1985). Группы конечного отражения . Дипломные тексты по математике. Том. 99. Спрингер. ISBN 978-0-387-96082-1 .
- Кейн, Ричард (2001). Группы отражения и теория инвариантов . Книги CMS по математике. Спрингер. ISBN 978-0-387-98979-2 . Збл 0986.20038 .
- Хиллер, Ховард (1982). Геометрия групп Кокстера . Исследования по математике. Том. 54. Питман. ISBN 978-0-273-08517-1 . Збл 0483.57002 .
- Винберг, Эрнест Б. (1984). «Отсутствие кристаллографических групп отражений в пространствах Лобачевского большой размерности». Труды Москов. Мат. Обще . 47 .










































![{\displaystyle \left[{\begin{smallmatrix}1&2\\2&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/054bbfab90f719d0a904fae9292bc247105f789a)
![{\displaystyle \left[{\begin{smallmatrix}1&3\\3&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/505977314de15df7c9fb5096120648c1f861a350)
![{\displaystyle \left[{\begin{smallmatrix}1&4\\4&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4471f2756c83398a1088eebdc9cde8f844d53d08)
![{\displaystyle \left[{\begin{smallmatrix}1&5\\5&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37defa42e8026365fed4a70df36e0fb468b828cd)
![{\displaystyle \left[{\begin{smallmatrix}1&6\\6&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cde9cd6357530022b8322b0a4ca1fcb8f74e9b4)
![{\displaystyle \left[{\begin{smallmatrix}1&\infty \\\infty &1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/192f1fbb798c42ad97af9447fe2ceb270e0bf613)
![{\displaystyle \left[{\begin{smallmatrix}1&3&2\\3&1&3\\2&3&1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf0db9a4f3239c976bce73f78dbf52c9f685a866)
![{\displaystyle \left[{\begin{smallmatrix}1&4&2\\4&1&3\\2&3&1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f41a04f428349f7258e67250191251a6ead6faa)
![{\displaystyle \left[{\begin{smallmatrix}1&3&2&2\\3&1&3&3\\2&3&1&2\\2&3&2&1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae791c94891e9f7294bc6880abf1d12241f13db3)
![{\displaystyle \left[{\begin{smallmatrix}1&3&2&3\\3&1&3&2\\2&3&1&3\\3&2&3&1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/338074fdd929504d5b226bdcb82874c8c454c23e)
![{\displaystyle \left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58d402f7fd38428fe2ac791f5a5d12bf7832c69f)
![{\displaystyle \left[{\begin{smallmatrix} \ \,2&-1\\-1&\ \,2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/201bbc13649b2a1b4b1af0ef827b8aeadf04a234)
![{\displaystyle \left[{\begin{smallmatrix}\ \,2&-{\sqrt {2}} \\-{\sqrt {2}}&\ \,2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb69aeb2e050dce68a86de7ac6439f2c75b4f576)
![{\displaystyle \left[{\begin{smallmatrix}\ \,2&-\phi \\-\phi &\ \,2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ad5939b99970521b908a38c78f758da820c0164)
![{\displaystyle \left[{\begin{smallmatrix}\ \,2&-{\sqrt {3}} \\-{\sqrt {3}}&\ \,2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bed5d4a647d3276389a2dc60ee21b71fc14f55f)
![{\displaystyle \left[{\begin{smallmatrix} \ \,2&-2\\-2&\ \,2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a0cd01abc91870eb2413feaaf4955f830426bb5)
![{\displaystyle \left[{\begin{smallmatrix}\ \,2&-1&\ \,0\\-1&\ \,2&-1\\\ \,0&-1&\ \,2\end{smallmatrix}} \верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b514ed28247e007abf2295bb4de0783bda9ae6fe)
![{\displaystyle \left[{\begin{smallmatrix}\ \,\ \ 2&-{\sqrt {2}}&\ \,0\\-{\sqrt {2}}&\ \,\ \ 2&-1 \\\ \,\ \ 0&\ \,-1&\ \,2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cf1c51c9ec65851aedc0fd2814d6df22557a0a2)
![{\displaystyle \left[{\begin{smallmatrix}\ \,2&-1&\ \,0&\ \,0\\-1&\ \,2&-1&-1\\\ \,0&-1&\ \,2& \ \,0\\\ \,0&-1&\ \,0&\ \,2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09f0c22e8717b8c83373ed2fbfc02c94bb7ba1f0)
![{\displaystyle \left[{\begin{smallmatrix}\ \,2&-1&\ \,0&-1\\-1&\ \,2&-1&\ \,0\\\ \,0&-1&\ \,2& -1\\-1&\ \,0&-1&\ \,2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45799dcc92560648c489533c208311daa848c5d8)












































































