Параболическая подгруппа группы отражений

В математической теории групп отражений параболические подгруппы представляют собой особый вид подгрупп . Точное определение того, какие подгруппы являются параболическими, зависит от контекста — например, обсуждается ли речь об общих группах Кокстера или группах комплексного отражения , — но во всех случаях набор параболических подгрупп демонстрирует важное хорошее поведение. Например, параболические подгруппы группы отражений имеют естественный набор индексов и образуют решетку при упорядочении по включению. Различные определения параболических подгрупп по существу совпадают в случае конечных вещественных групп отражений. Параболические подгруппы возникают в теории алгебраических групп благодаря их связи с группами Вейля .

Предыстория: группы отражения

В евклидовом пространстве (например, евклидова плоскость , обычное трехмерное пространство или многомерные аналоги) отражение — это симметрия пространства по отношению к зеркалу (технически, по подпространству размером на единицу меньше, чем все пространство). который фиксирует векторы, лежащие на зеркале, и отправляет векторы, ортогональные зеркалу, в их отрицательные значения. Конечная вещественная группа отражений W — это конечная группа, порожденная отражениями (т. е. каждое линейное преобразование в W является композицией некоторых отражений в W ). Например, симметрии правильного многоугольника на плоскости образуют группу отражений (называемую группой диэдра ), поскольку каждая симметрия вращения многоугольника представляет собой композицию двух отражений. Конечные группы вещественных отражений можно обобщать различными способами. и определение параболической подгруппы зависит от выбора определения.

Каждая конечная вещественная группа отражений W имеет структуру группы Кокстера : это означает, что W содержит подмножество S отражений (называемых простыми отражениями ), такое что S порождает W , подчиняясь отношениям вида $$W=\langle S\mid (ss')^{m_{s,s'}}=1\rangle ,$$ где 1 обозначает единицу в W , а $m_{s,s'}$ это числа, которые удовлетворяют $m_{s,s}=1$ для $s\in S$ и $m_{s,s'}\in \{2,3,\ldots \}$ для $s\neq s'\in S$. Таким образом, группы Кокстера образуют одно обобщение конечных вещественных групп отражений.

Отдельное обобщение состоит в рассмотрении геометрического действия на векторных пространствах , базовым полем которых не являются действительные числа . В частности, если заменить действительные числа комплексными числами с соответствующим обобщением понятия отражения, можно прийти к определению комплексной группы отражений . Любую действительную группу отражений можно комплексифицировать , чтобы получить комплексную группу отражений, поэтому комплексные группы отражений образуют еще одно обобщение конечных вещественных групп отражений.

В группах Кокстера

Решетка стандартных параболических подгрупп симметрической группы S ₄ , порожденная как группа Кокстера простыми отражениями s ₁ = (1 2) , s ₂ = (2 3) и s ₃ = (3 4) ( смежные транспозиции ), с единичным элементом ι

Предположим, что W — группа Кокстера с конечным множеством S простых отражений. Для каждого подмножества I из S пусть $W_{I}$ обозначим подгруппу W, порожденную $I$. подгруппы называются стандартными параболическими подгруппами группы W. Такие В крайних случаях, $W_{\varnothing }$ - тривиальная подгруппа (содержащая только элемент W единичный ) и $W_{S}=W$.

Пара $(W_{I},I)$ снова группа Кокстера. Более того, групповая структура Кокстера на $W_{I}$ совместимо с этим на W в следующем смысле: если $\ell _{S}$ обозначает функцию длины на W относительно S (так что $\ell _{S}(w)=k$ если элемент w из W можно записать как произведение k элементов из S и не менее), то для каждого элемента w из $W_{I}$, у одного это есть $\ell _{S}(w)=\ell _{I}(w)$. То есть длина w одинакова независимо от того, рассматривается ли она как элемент W или как элемент $W_{I}$. То же самое верно и для порядка Брюа : если u и w — элементы $W_{I}$, затем $u\leq w$ в приказе Брюа о $W_{I}$ тогда и только тогда, когда $u\leq w$ в порядке Брюа на W .

Если I и J — два подмножества S , то $W_{I}=W_{J}$ тогда и только тогда, когда $I=J$, $W_{I}\cap W_{J}=W_{I\cap J}$и самая маленькая группа $\langle W_{I},W_{J}\rangle$ который содержит оба $W_{I}$ и $W_{J}$ является $W_{I\cup J}$. Следовательно, решетка стандартных параболических подгрупп группы W является булевой решеткой .

Дана стандартная параболическая подгруппа $W_{I}$ группы W смежные классы Кокстера $W_{I}$ в W имеют особенно хорошую систему представителей: пусть $W^{I}$ обозначим множество $$W^{I}=\{w\in W\colon \ell _{S}(ws)>\ell _{S}(w){\text{ for all }}s\in I\}$$элементов из W , не имеющих ни одного элемента из I, как прямого спуска. Тогда для каждого $w\in W$, есть уникальные элементы $u\in W^{I}$ и $v\in W_{I}$ такой, что $w=uv$. Причём это аддитивное произведение по длине, т.е. $\ell _{S}(w)=\ell _{S}(u)+\ell _{S}(v)$. Кроме того, u — элемент минимальной длины в смежном классе $wW_{I}$. Аналогичная конструкция справедлива и для правых смежных классов. Совокупность всех левых смежных классов стандартных параболических подгрупп является одной из возможных конструкций комплекса Кокстера .

В терминах диаграммы Кокстера-Дынкина стандартные параболические подгруппы возникают путем взятия подмножества узлов диаграммы и ребер, созданных между этими узлами, стирая все остальные. Единственные нормальные параболические подгруппы возникают в результате объединения связных компонентов диаграммы, а вся группа W является прямым произведением неприводимых групп Кокстера , соответствующих компонентам.

В группах сложных отражений

Решетка параболических подгрупп группы диэдра D _2×4 , представленная как вещественная группа отражений, состоит из тривиальной подгруппы, четырех двухэлементных подгрупп, порожденных одним отражением, и всей группы. Упорядоченные по включению, они дают ту же решетку, что и решетка фиксированных пространств, упорядоченных обратным включением.

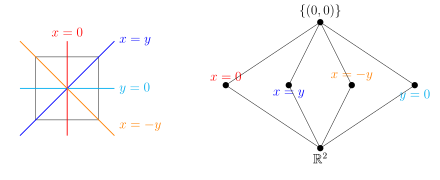
Предположим, что W — комплексная группа отражений, действующая в комплексном векторном пространстве V . Для любого подмножества $A\subseteq V$, позволять $$W_{A}=\{w\in W\colon w(a)=a{\text{ for all }}a\in A\}$$— подмножество W, состоящее из тех элементов W , которые фиксируют каждый элемент A . подгруппа называется параболической подгруппой группы W. Такая В крайних случаях, $W_{\varnothing }=W_{\{0\}}=W$ и $W_{V}$ — тривиальная подгруппа группы W , содержащая только единичный элемент.

Из теоремы Стейнберга (1964) следует , что каждая параболическая подгруппа $W_{A}$ комплексной группы отражений W — это группа отражений, порожденная отражениями в W , которые фиксируют каждую точку в A . Поскольку W действует линейно на V , $W_{A}=W_{\overline {A}}$ где ${\overline {A}}$ является промежутком A линейным (то есть наименьшим подпространством V , содержащим A ). Фактически, существует простой выбор подпространств A , индексирующих параболические подгруппы: каждое отражение в W фиксирует гиперплоскость (то есть подпространство V , размерность которого на 1 меньше, чем у V ) поточечно, а совокупность всех этих гиперплоскости — отражений W. это расположение Совокупность всех пересечений подмножеств этих гиперплоскостей, частично упорядоченный по включению, представляет собой решетку $L_{W}$. Элементами решетки являются в точности фиксированные пространства элементов W (т. е. для каждого пересечения I отражающих гиперплоскостей существует элемент $w\in W$ такой, что $\{v\in V\colon w(v)=v\}=I$). Карта, которая отправляет $I\mapsto W_{I}$ для $I\in L_{W}$ является изменяющей порядок биекцией между подпространствами в $L_{W}$ и параболические подгруппы W .

Согласованность определений в конечных группах вещественных отражений

Пусть W — конечная вещественная группа отражений; то есть W — конечная группа линейных преобразований в конечномерном действительном евклидовом пространстве , порожденная ортогональными отражениями. Как упоминалось выше (см. § Предыстория: группы отражений ), W можно рассматривать как группу Кокстера, так и как комплексную группу отражений. Для реальной группы отражений W параболические подгруппы W (рассматриваемые как комплексная группа отражений) не являются всеми стандартными параболическими подгруппами W (если рассматривать их как группу Кокстера, после указания фиксированного порождающего набора Кокстера S ), поскольку существует множество больше подпространств в решетке пересечений его расположения отражений, чем подмножества S . Однако в конечной вещественной группе отражений W каждая параболическая подгруппа сопряжена стандартной параболической подгруппе относительно S .

Примеры

Решетка параболических подгрупп группы S ^Б
₄ , представленный как знаковые перестановки {−2, −1, 1, 2}, с тождеством ι

Симметричная группа $S_{n}$, который состоит из перестановок всех $\{1,\ldots ,n\}$, является группой Кокстера относительно множества смежных транспозиций $(1\ 2)$, ..., $(n-1\ n)$. Стандартные параболические подгруппы $S_{n}$ (которые также известны как подгруппы Янга ) — это подгруппы вида $S_{a_{1}}\times \cdots \times S_{a_{k}}$, где $a_{1},\ldots ,a_{k}$ — положительные целые числа с суммой n , в которых первый множитель прямого произведения меняет местами элементы $\{1,\ldots ,a_{1}\}$ между собой второй фактор переставляет местами элементы $\{a_{1}+1,\ldots ,a_{1}+a_{2}\}$ между собой и так далее.

Гипероктаэдрическая группа $S_{n}^{B}$, который состоит из всех знаковых перестановок $\{\pm 1,\ldots ,\pm n\}$ (то есть биекции w на этом множестве такие, что $w(-i)=-w(i)$ для всех i ), имеет в качестве максимальных стандартных параболических подгрупп стабилизаторы группы $\{i+1,\ldots ,n\}$ для $i\in \{1,\ldots ,n\}$.

Более общие определения в теории Кокстера

В группе Кокстера, порожденной конечным множеством S простых отражений, можно определить параболическую подгруппу как любую сопряженную стандартную параболическую подгруппу. Согласно этому определению, по-прежнему верно, что пересечение любых двух параболических подгрупп является параболической подгруппой. То же самое , вообще говоря, не справедливо для групп Кокстера бесконечного ранга.

Если W — группа, а T — подмножество W , пара $(W,T)$ называется двойственной системой Кокстера, если существует подмножество S в T такое, что $(W,S)$ представляет собой систему Кокстера и $$T=\{wsw^{-1}\colon w\in W,s\in S\},$$так что T — множество всех отражений (сопряженных с простыми отражениями) W. в Для двойной системы Кокстера $(W,T)$, подгруппа W называется параболической подгруппой, если она является стандартной параболической (как в § В группах Кокстера ) группы $(W,S)$ для некоторого выбора простых отражений S для $(W,T)$.

В некоторых двойственных системах Кокстера все множества простых отражений сопряжены друг с другом; в этом случае параболические подгруппы относительно одной простой системы (т. е. сопряженные стандартным параболическим подгруппам) совпадают с параболическими подгруппами относительно любой другой простой системы. Однако даже в конечных примерах это может не выполняться: например, если W — группа диэдра с 10 элементами, рассматриваемая как симметрии правильного пятиугольника , а T — множество симметрий отражений многоугольника, то любая пара отражений в T образует простую систему для $(W,T)$, но не все пары отражений сопряжены друг с другом. Тем не менее, если W конечна, то параболические подгруппы (в указанном выше смысле) совпадают с параболическими подгруппами в классическом смысле (т. е. сопряженными стандартными параболическими подгруппами относительно одного фиксированного выбора простых отражений S ). Тот же результат, вообще говоря, не верен для бесконечных групп Кокстера.

Аффинные и кристаллографические группы Кокстера

Когда W — аффинная группа Кокстера , ассоциированная конечная группа Вейля всегда является максимальной параболической подгруппой, диаграмма Кокстера-Дынкина которой является результатом удаления одного узла из W. диаграммы В частности, функции длины на конечной и аффинной группах совпадают. Фактически, каждая стандартная параболическая подгруппа аффинной группы Кокстера конечна. Как и в случае конечных вещественных групп отражений, когда мы рассматриваем действие аффинной группы Кокстера W на евклидовом пространстве V , сопряженными стандартными параболическими подгруппами группы W являются в точности подгруппы вида $$\{w\in W\colon w(a)=a{\text{ for all }}a\in A\}$$для некоторого подмножества A из V .

Если W — кристаллографическая группа Кокстера, тогда каждая параболическая подгруппа группы W также является кристаллографической.

Связь с теорией алгебраических групп

Если G — алгебраическая группа , а B — борелевская подгруппа для G , то параболическая подгруппа в G — это любая подгруппа, B. содержащая Если, кроме того, G имеет ( B , N ) пару , то соответствующая факторгруппа $W=B/(B\cap N)$ является группой Кокстера, называемой группой Вейля группы G . Тогда группа G имеет разложение Брюа $G=\bigsqcup _{w\in W}BwB$ на двойные смежные классы (где $\sqcup$ — дизъюнктное объединение ), а параболические подгруппы группы G , содержащие B, — это в точности подгруппы вида $$P_{J}=BW_{J}B$$где $W_{J}$ — стандартная параболическая подгруппа W. группы

Параболические замыкания

Предположим, что W — группа Кокстера конечного ранга (т. е. множество S простых образующих конечно). Учитывая любое подмножество X группы W , можно определить параболическое замыкание X содержащих как пересечение всех параболических подгрупп X. , Как упоминалось выше, в этом случае пересечение любых двух параболических подгрупп группы W снова является параболической подгруппой группы W , и, следовательно, параболическое замыкание группы X является параболической подгруппой группы W ; в частности, это (единственная) минимальная параболическая подгруппа W , содержащая X . Тот же анализ применим к комплексным группам отражений, где параболическое замыкание X также является поточечным стабилизатором пространства неподвижных точек X . Этого нельзя сказать о группах Кокстера бесконечного ранга.

Группы кос

Каждая группа Кокстера связана с другой группой, называемой ее группой Артина-Титса или обобщенной группой кос , которая определяется путем исключения соотношений $s^{2}=1$ для каждого генератора $s\in S$ из презентации в Коксете. Хотя обобщенные группы кос не являются группами отражений, они наследуют понятие параболических подгрупп: стандартная параболическая подгруппа обобщенной группы кос — это подгруппа, порожденная подмножеством стандартного порождающего множества S , а параболическая подгруппа — это любая подгруппа, сопряженная с стандартная параболика.

Говорят, что обобщенная группа кос имеет сферический тип , если связанная с ней группа Кокстера конечна. Если B — обобщенная группа кос сферического типа, то пересечение любых двух параболических подгрупп группы B также является параболической подгруппой. Следовательно, параболические подгруппы группы B образуют решетку по включению.

Для конечной вещественной группы отражений W соответствующая обобщенная группа кос может быть определена на чисто топологическом языке, без ссылки на конкретное представление группы. Это определение естественным образом распространяется на конечные комплексные группы отражений. В этой настройке также можно определить параболические подгруппы.

Ссылки

• Баумайстер, Барбара; Дайер, Мэтью; Стамп, Кристиан; Вегенер, Патрик (2014), «Заметка о транзитивном действии Гурвица на разложение параболических элементов Кокстера», Труды Американского математического общества , серия B, 1 (13): 149–154, arXiv : 1402.2500 , doi : 10.1090/ С2330-1511-2014-00017-1
• Баумайстер, Барбара; Гобе, Томас; Робертс, Киран; Вегенер, Патрик (2017), «О действии Гурвица в конечных группах Кокстера», J. Group Theory , 20 (1): 103–131, arXiv : 1512.04764 , doi : 10.1515/jgth-2016-0025 , S2CID   44035800
• Бьёрнер, Андерс ; Бренти, Франческо (2005), Комбинаторика групп Кокстера , Springer, doi : 10.1007/3-540-27596-7 , ISBN  978-3540-442387 , S2CID   115235335
• Борель, Арманд (2001), Очерки истории групп Ли и алгебраических групп , История математики, том. 21, Американское математическое общество и Лондонское математическое общество, ISBN.  0-8218-0288-7
• Бруэ, Мишель (2010), Введение в группы комплексного отражения и их группы кос , Конспекты лекций по математике, том. 1988, Springer-Verlag, номер документа : 10.1007/978-3-642-11175-4 , ISBN.  978-3-642-11174-7
• Чоу, Тимоти (2010), «Почему параболические подгруппы называются «параболическими подгруппами»?» , MathOverflow и др. , получено 16 февраля 2024 г.
• Камплидо, Мария; Гебхардт, Волкер; Гонсалес-Менесес, Хуан; Вист, Берт (2019), «О параболических подгруппах групп Артина – Титса сферического типа», Advances in Mathematics , 352 : 572–610, arXiv : 1712.06727 , doi : 10.1016/j.aim.2019.06.010
• Динь, Франсуа; Мишель, Жан (1991), Представления конечных групп лиева типа , Студенческие тексты Лондонского математического общества, том. 21, Издательство Кембриджского университета, ISBN  0-521-40117-8
• Гобе, Томас (2017), «О циклических разложениях в группах Кокстера» , Sém. Лотар. Комбинировать. , 78Б : Ст. 45, arXiv : 1611.03442
• Годеман, Роджер (1961), «Линейные алгебраические группы на совершенном поле», Семин. Бурбаки , 13
• Гонсалес-Менесес, Хуан; Марин, Иван (2022), Параболические подгруппы групп комплексных кос I , arXiv : 2208.11938v1
• Хамфрис, Джеймс Э. (1990), Группы отражения и группы Кокстера , Cambridge University Press, doi : 10.1017/CBO9780511623646 , ISBN  0-521-37510-Х , S2CID   121077209
• Кейн, Ричард (2001), Группы отражений и теория инвариантов , Книги CMS по математике/Ouvrages de Mathématiques de la SMC, Springer-Verlag, doi : 10.1007/978-1-4757-3542-0 , ISBN  0-387-98979-Х , S2CID   119694827
• Лерер, Густав И.; Тейлор, Дональд Э. (2009), Унитарные группы отражения , Серия лекций Австралийского математического общества, том. 20, Издательство Кембриджского университета , ISBN  978-0-521-74989-3
• Маккаммонд, Джон; Салуэй, Роберт (2017), «Группы Артина евклидова типа», Invent. Математика. , 210 (1): 231–282, arXiv : 1312.7770 , Bibcode : 2017InMat.210..231M , doi : 10.1007/s00222-017-0728-2 , S2CID   253738806
• Нуида, Кодзи (2012), «Локально параболические подгруппы в группах Кокстера произвольных рангов», Journal of Algebra , 350 : 207–217, arXiv : 1006.4709 , doi : 10.1016/j.jalgebra.2011.11.005
• Орлик, Петр ; Терао, Хироаки (1992), Расположение гиперплоскостей , Основы математических наук, Springer, doi : 10.1007/978-3-662-02772-1 , ISBN  978-3-540-55259-8
• Райнер, Виктор; Риполь, Вивьен; Стамп, Кристиан (2017), «О несопряженных элементах Кокстера в хорошо сгенерированных группах отражений», Math. З. , 285 (3–4): 1041–1062, arXiv : 1404.5522 , doi : 10.1007/s00209-016-1736-4 , S2CID   253752187
• Стейнберг, Роберт (1964), «Дифференциальные уравнения, инвариантные относительно конечных групп отражений», Труды Американского математического общества , 112 (3): 392–400, doi : 10.1090/S0002-9947-1964-0167535-3
• Тейлор, DE (2012), «Подгруппы отражений конечных комплексных групп отражений», Journal of Algebra , 366 : 218–234, arXiv : 1201.1348 , doi : 10.1016/j.jalgebra.2012.04.033