Комплекс Коксетера

В математике комплекс Кокстера , названный в честь HSM Coxeter , представляет собой геометрическую структуру ( симплициальный комплекс ), связанную с группой Кокстера . Комплексы Кокстера являются базовыми объектами, позволяющими возводить здания ; они образуют квартиры здания.

Строительство

Каноническое линейное представление

Первый ингредиент в построении комплекса Кокстера, связанный с системой Кокстера. $(W,S)$ определенным представлением является $W$, называемое каноническим представлением $W$.

Позволять $(W,S)$ быть системой Кокстера с матрицей Кокстера $M=(m(s,t))_{s,t\in S}$. Каноническое представление задается векторным пространством $V$ на основе формальных символов $(e_{s})_{s\in S}$, который имеет симметричную билинейную форму $B(e_{s},e_{t})=-\cos \left({\frac {\pi }{m(s,t)}}\right)$. В частности, $B(e_{s},e_{s})=1$. Действие $W$ на $V$ затем дается $s(v)=v-2B(e_{s},v)e_{s}$.

Это представление имеет несколько фундаментальных свойств в теории групп Кокстера; например, $B$ положительно определен тогда и только тогда, когда $W$ конечно. Это верное представление $W$.

Камеры и конус Титса

Это представление описывает $W$ как группа размышлений , с оговоркой, что $B$ может не быть положительно определенным. Тогда становится важным различать представление $V$ от его двойного $V^{*}$. Векторы $e_{s}$ роды $V$ и иметь соответствующие двойственные векторы $e_{s}^{\vee }$ в $V^{*}$ данный

$\langle e_{s}^{\vee },v\rangle =2B(e_{s},v),$

где угловые скобки указывают на естественное спаривание между $V^{*}$ и $V$.

Сейчас $W$ действует на $V^{*}$ и действие задается

$s(f)=f-\langle f,e_{s}\rangle e_{s}^{\vee },$

для $s\in S$ и любой $f\in V^{*}$. Затем $s$ это отражение в гиперплоскости $H_{s}=\{f\in V^{*}:\langle f,e_{s}\rangle =0\}$. У одного есть основная камера ${\mathcal {C}}=\{f\in V^{*}:\langle f,e_{s}\rangle >0\ \forall s\in S\}$; это лица так называемых стен, $H_{s}$. Остальные камеры можно получить из ${\mathcal {C}}$ в переводе: они $w{\mathcal {C}}$ для $w\in W$.

Конус Титса ​ $X=\bigcup _{w\in W}w{\overline {\mathcal {C}}}$. Это не обязательно должно быть все $V^{*}$. Большое значение имеет тот факт, что $X$ является выпуклым. Закрытие ${\overline {\mathcal {C}}}$ из ${\mathcal {C}}$ является фундаментальной областью действия $W$ на $X$.

Комплекс Кокстера

Комплекс Кокстера $\Sigma (W,S)$ из $W$ относительно $S$ является $\Sigma (W,S)=(X\setminus \{0\})/\mathbb {R} _{+}$, где $\mathbb {R} _{+}$ — это мультипликативная группа положительных реалий.

Примеры

Конечные диэдральные группы

Группы диэдра $D_{n}$ (порядка 2 n ) являются группами Кокстера соответствующего типа $\mathrm {I} _{2}(n)$. У них есть презентация $\left\langle s,t\,\left|\,s^{2},t^{2},(st)^{n}\right\rangle \right.$.

Каноническое линейное представление $\mathrm {I} _{2}(n)$ - это обычное отражение группы диэдра, действующей на $n$-гон в плоскости (так $V=\mathbb {R} ^{2}$ в этом случае). Например, в случае $n=3$ получаем группу Кокстера типа $\mathrm {I} _{2}(3)=\mathrm {A} _{2}$, действующий на равносторонний треугольник в плоскости. Каждое отражение $s$ имеет связанную гиперплоскость $H_{s}$ в двойственном векторном пространстве (которое можно канонически отождествить с самим векторным пространством, используя билинейную форму $B$, который в данном случае является внутренним продуктом, как отмечалось выше); это стены. Вырезали камеры, как показано ниже:

Комплекс Кокстера тогда является соответствующим $2n$-gon, как на изображении выше. Это симплициальный комплекс размерности 1, и его можно раскрасить по котипу.

Бесконечная группа диэдра

Другой мотивирующий пример — бесконечная группа диэдра. $D_{\infty }$. Это можно рассматривать как группу симметрий вещественной прямой, которая сохраняет набор точек с целочисленными координатами; оно порождается отражениями в $x=0$ и $x={1 \over 2}$. В этой группе есть презентация Кокстера. $\left\langle s,t\,\left|\,s^{2},t^{2}\right\rangle \right.$.

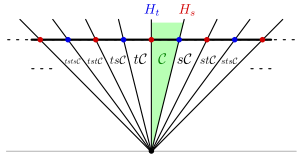
В этом случае уже невозможно идентифицировать $V$ с его двойным пространством $V^{*}$, как $B$ является вырожденным. Тогда лучше работать исключительно с $V^{*}$, где определяются гиперплоскости. Тогда получается следующая картина:

В этом случае конус Титса — это не вся плоскость, а только верхняя полуплоскость. При частном по положительным числам получается еще одна копия действительной линии с отмеченными точками на целых числах. Это комплекс Кокстера бесконечной группы диэдра.

Альтернативное строительство комплекса Коксетера

В другом описании комплекса Кокстера используются стандартные классы группы Кокстера. $W$. Стандартный смежный класс - это смежный класс вида $wW_{J}$, где $W_{J}=\langle J\rangle$ для некоторого правильного подмножества $J$ из $S$. Например, $W_{S}=W$ и $W_{\emptyset }=\{1\}$.

Комплекс Кокстера $\Sigma (W,S)$ тогда является ЧУМ стандартных смежных классов, упорядоченных обратным включением. Он имеет каноническую структуру симплициального комплекса, как и все частично упорядоченные множества, удовлетворяющие:

• Любые два элемента имеют максимальную нижнюю границу.
• ЧУ-множество элементов, меньших или равных любому данному элементу, изоморфно ЧУ-множеству подмножеств $\{1,2,\ldots ,n\}$ для некоторого целого числа n .

Характеристики

Комплекс Кокстера, связанный с $(W,S)$ имеет размерность $|S|-1$. Он гомеоморфен $(|S|-1)$-сфера, если W конечна, и сжимаема , если W бесконечна.

Каждая квартира сферического здания Титса представляет собой комплекс Кокстера.

См. также

• Здания
• Группа Вейля
• Корневая система

Источники

• Питер Абраменко и Кеннет С. Браун , Здания, теория и приложения . Спрингер, 2008.