Гипероктаэдрическая группа

Группа $C 2$ имеет порядок 8, как показано на этом кружке.	Группа $C 3$ ( $Oh) имеет порядок 48 ,$ как показано этими сферическими треугольными областями отражения .

В математике гипероктаэдрическая группа важный тип группы , который может быть реализован как группа симметрий гиперкуба — или перекрестного многогранника . Название ему дал Альфред Янг в 1930 году. Группы этого типа идентифицируются параметром $n$ — размерностью гиперкуба.

Как группа Кокстера она имеет тип $Bn группа = Cn,$ а как Вейля она связана с симплектическими группами и с ортогональными группами в нечетных размерностях. Как изделие венок это $S_{2}\wr S_{n}$ где $Sn n$ — группа степени $симметрическая$ . Как группа перестановок , группа представляет собой знаковую симметрическую группу перестановок π либо из множества $\{-n,-n+1,\cdots ,-1,1,2,\cdots ,n\}$ или из множества $\{-n,-n+1,\cdots ,n\}$ такой, что $\pi (i)=-\pi (-i)$ для всех $я$ . Как группу матриц , ее можно описать как группу $n \times n,$ ортогональных матриц размера все элементы которых являются целыми числами . Эквивалентно, это набор $матриц размера n \times n$ с элементами только 0, 1 или –1, которые являются обратимыми и имеют ровно один ненулевой элемент в каждой строке или столбце. Теория представлений гипероктаэдрической группы была описана ( Янг 1930 ) согласно ( Кербер 1971 , стр. 2).

В трех измерениях гипероктаэдрическая группа известна как $O \times S 2$ , где $O ≅ S 4$ — октаэдрическая группа , а $S 2$ — симметричная группа (здесь циклическая группа ) порядка 2. Геометрические фигуры в трех измерениях с этой группой симметрии. Говорят, что они обладают октаэдрической симметрией , названной в честь правильного октаэдра , или 3- ортоплекса . В 4-х измерениях это называется гексадекахорной симметрией , в честь обычного 16-ячеечного или 4- ортоплекса . В двух измерениях структура гипероктаэдрической группы представляет собой абстрактную группу диэдра восьмого порядка , описывающую симметрию квадрата или 2-ортоплекса.

По размеру [ править ]

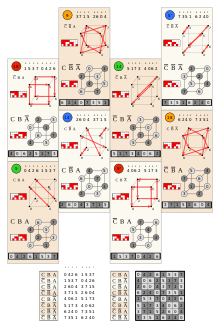
Гипероктаэдрические группы могут быть названы как B _n , в скобках или как граф группы Кокстера:

н	Симметрия группа	Б _н	Обозначение Кокстера		Заказ	Зеркала	Структура	Связанные правильные многогранники
2	Д ₄ (*4•)	B_Б2	[4]		2 ²2! = 8	4	$Dih_{4}$ $\cong S_{2}\wr S_{2}$	Квадрат , восьмиугольник
3	О _ч ( *432 )	B_Б3	[4,3]		2 ³3! = 48	3+6	$S_{4}\times S_{2}$ $\cong S_{2}\wr S_{3}$	Куб , октаэдр
4	± ¹/ ₆[OxO].2 ^[1] (O/V;O/V) ^* ^[2]	Б ₄	[4,3,3]		2 ⁴4! = 384	4+12	$S_{2}\wr S_{4}$	Тессеракт , 16-ячеечный , 24-ячеечный
5		Б ₅	[4,3,3,3]		2 ⁵5! = 3840	5+20	$S_{2}\wr S_{5}$	5-куб , 5-ортоплекс
6		Б ₆	[4,3 ⁴]		2 ⁶6! = 46080	6+30	$S_{2}\wr S_{6}$	6-куб , 6-ортоплекс
...н		Б _н	[4,3 ^n-2]	...	2 ^нн ! = (2n ) !!	н ²	$S_{2}\wr S_{n}$	гиперкуб , ортоплекс

Подгруппы [ править ]

Существует примечательная подгруппа индекса два, соответствующая группе Кокстера D _n и симметриям полугиперкуба . Если рассматривать его как сплетение, то существуют два естественных отображения гипероктаэдрической группы в циклическую группу порядка 2: одно отображение, возникающее в результате «перемножения знаков всех элементов» (в n копиях $\{\pm 1\}$ ), и одна карта, полученная из четности перестановки. Умножив их вместе, получим третью карту. $C_{n}\to \{\pm 1\}$ . Ядро первого отображения — группа Коксетера. $D_{n}.$ С точки зрения знаковых перестановок , рассматриваемых как матрицы, эта третья карта является просто определителем, в то время как первые две соответствуют «умножению ненулевых записей» и «четности базовой (беззнаковой) перестановки», которые в целом не имеют смысла. для матриц, но находятся в корпусе из-за совпадения со сплетением.

Ядрами этих трех отображений являются все три подгруппы индекса два гипероктаэдрической группы, как обсуждается в H1 _{разделе} : Абелианизация ниже, а их пересечение является производной подгруппой индекса 4 (факторизируем 4-группу Клейна), что соответствует вращательная симметрия демигиперкуба.

В другом направлении центром является подгруппа скалярных матриц {±1}; геометрически факторизация по этому соответствует переходу к проективной ортогональной группе .

В размерности 2 эти группы полностью описывают гипероктаэдрическую группу, которая представляет собой группу диэдра Dih ₄ порядка 8 и является расширением 2.V (4-группы циклической группой порядка 2). В общем случае переход к подфактору (производная подгруппа, mod-центр) — это группа симметрии проективного демигиперкуба.

Гипероктаэдрическая n подгруппа, D _по размерности:

н	Симметрия группа	Д _н	Обозначение Кокстера		Заказ	Зеркала	Связанные многогранники
2	Д ₂ (*2•)	D_Д2	[2] = [ ]×[ ]		4	2	Прямоугольник
3	Т _д ( *332 )	Д ₃	[3,3]		24	6	тетраэдр
4	± ¹/ ₃[Tx T ].2 ^[1] (T/V;T/V) ₋^* ^[3]	Д ₄	[3 ^1,1,1]		192	12	16-ячеечный
5		Д ₅	[3 ^2,1,1]		1920	20	5-демикуб
6		Д ₆	[3 ^3,1,1]		23040	30	6-демикуб
...н		Д _н	[3 ^н-3,1,1]	...	2 ^n-1н!	п(п-1)	полугиперкуб

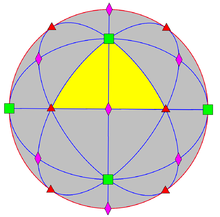
Киральная гипероктаэдрическая симметрия — прямая подгруппа гипероктаэдрической симметрии с индексом 2.

н	Симметрия группа	Обозначение Кокстера		Заказ
2	С ₄ (4•)	[4] ⁺		4
3	О ( 432 )	[4,3] ⁺		24
4	¹/ ₆[O×O].2 ^[1] (O/V;O/V) ^[4]	[4,3,3] ⁺		192
5		[4,3,3,3] ⁺		1920
6		[4,3,3,3,3] ⁺		23040
...н		[4,(3 ^n-2) ⁺]	...	2 ^n-1н!

Еще одну заметную подгруппу индекса 2 можно назвать гиперпиритоэдрической симметрией по размерности: ^[5] Эти группы имеют n ортогональных зеркал в n -мерностях.

н	Симметрия группа	Обозначение Кокстера		Заказ	Зеркала	Связанные многогранники
2	Д ₂ (*2•)	[4,1 ⁺]=[2]		4	2	Прямоугольник
3	Т _ч ( 3*2 )	[4,3 ⁺]		24	3	курносый октаэдр
4	± ¹/ ₃[T×T].2 ^[1] (T/V;T/V) ^* ^[6]	[4,(3,3) ⁺]		192	4	курносый 24-клеточный
5		[4,(3,3,3) ⁺]		1920	5
6		[4,(3,3,3,3) ⁺]		23040	6
...н		[4,(3 ^n-2) ⁺]	...	2 ^n-1н!	н

Гомология [ править ]

Групповая гомология гипероктаэдрической группы аналогична гомологии симметричной группы и демонстрирует стабилизацию в смысле стабильной теории гомотопий .

H ₁ : абелианизация [ править ]

Первая группа гомологий, которая согласуется с абелианизацией , стабилизируется в четырехгруппе Клейна и определяется выражением:

H_{1}(C_{n},\mathbf {Z} )={\begin{cases}0&n=0\\\mathbf {Z} /2&n=1\\\mathbf {Z} /2\times \mathbf {Z} /2&n\geq 2\end{cases}}.

Это легко увидеть непосредственно: $-1$ элементы имеют порядок 2 (который непустой для $n\geq 1$ ), и все они сопряжены, как и транспозиции в $S_{n}$ (который непуст для $n\geq 2$ ), и это два отдельных класса. Эти элементы порождают группу, поэтому единственные нетривиальные абелианизации относятся к 2-группам, и любой из этих классов может быть отправлен независимо в $-1\in \{\pm 1\},$ поскольку это два отдельных класса. Карты явно даны как «произведение знаков всех элементов» (в n экземплярах $\{\pm 1\}$ ) и знак перестановки. Умножение их вместе дает третью нетривиальную карту ( определитель матрицы, который отправляет оба этих класса в $-1$ ), и вместе с тривиальным отображением они образуют 4-группу.

H ₂ : Множители Шура [ править ]

Вторые группы гомологии, классически известные как множители Шура , были вычислены в ( Ihara & Yokonuma 1965 ).

Они есть:

H_{2}(C_{n},\mathbf {Z} )={\begin{cases}0&n=0,1\\\mathbf {Z} /2&n=2\\(\mathbf {Z} /2)^{2}&n=3\\(\mathbf {Z} /2)^{3}&n\geq 4\end{cases}}.

Примечания [ править ]

^ Jump up to: Перейти обратно: ^а ^б ^с ^д Конвей и Смит, 2003 г.
^ Выборы 1964 , № 47
^ du Election 1964 , № 42
^ Выборы 1964 , № 27
^ Коксетер 1999 , с. 121, Сочинение 5 Правильные перекошенные многогранники
^ du Election 1964 , № 41

Ссылки [ править ]

Миллер, Джорджия (1918). «Группы, образованные специальными матрицами» . Бык. Являюсь. Математика. Соц . 24 (4): 203–6. дои : 10.1090/S0002-9904-1918-03043-7 .
дю Валь, П. (1964). Гомографии, кватернионы и вращения . Оксфордские математические монографии. Кларендон Пресс. ОСЛК 904102141 .
Ихара, Син-итиро; Йоконума, Такео (1965), «О вторых группах когомологий (мультипликаторах Шура) конечных групп отражений», Журнал факультета естественных наук. Токийский университет. Раздел ИА. Математика , 11 : 155–171, ISSN 0040-8980 , МР 0190232.
Кербер, Адальберт (1971), Представления групп перестановок. I , Конспект лекций по математике, вып. 240, Springer-Verlag , номер документа : 10.1007/BFb0067943 , ISBN. 978-3-540-05693-5 , МР 0325752
Кербер, Адальберт (1975), Представления групп перестановок. II , Конспекты лекций по математике, вып. 495, Springer-Verlag , номер домена : 10.1007/BFb0085740 , ISBN. 978-3-540-07535-6 , МР 0409624
Янг, Альфред (1930), «О количественном анализе замещения 5» , Труды Лондонского математического общества , серия 2, 31 : 273–288, doi : 10.1112/plms/s2-31.1.273 , ISSN 0024-6115 , JFM 56.0135 .02
Коксетер, HSM; Мозер, WOJ (2013) [1980]. Генераторы и отношения для дискретных групп (4-е изд.). Спрингер. п. 92 §7.4 Линейные дробные группы, с. 122 §9.3 Конечные группы. ISBN 978-3-662-21943-0 .
Бааке, М. (1984). «Структура и представления гипероктаэдрической группы». Дж. Математика. Физ . 25 (11): 3171. Бибкод : 1984JMP....25.3171B . дои : 10.1063/1.526087 .
Стембридж, Джон Р. (1992). «Проективные представления гипероктаэдрической группы». Дж. Алгебра . 145 (2): 396–453. дои : 10.1016/0021-8693(92)90110-8 . hdl : 2027.42/30235 .
Коксетер, HSM (1999). Красота геометрии: двенадцать эссе . Дувр. ISBN 0-486-40919-8 . LCCN 99035678 .
Конвей, Джон Х .; Смит, Дерек А. (2003). О кватернионах и октонионах . ЦРК Пресс. ISBN 978-1-000-68777-4 .

[Conway03-1] Jump up to: Перейти обратно: ^а ^б ^с ^д Конвей и Смит, 2003 г.

[2] Выборы 1964 , № 47

[3] u Election 1964 , № 42

[4] Выборы 1964 , № 27

[5] Коксетер 1999 , с. 121, Сочинение 5 Правильные перекошенные многогранники

[6] u Election 1964 , № 41

[1]

[2]

[3]

[4]

[5]

[6]