7-симплекс

Обычный октаэксон (7-симплекс)
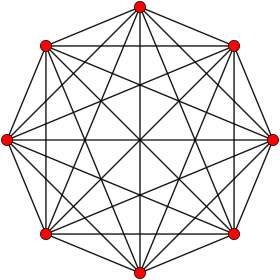Ортогональная проекция внутри многоугольника Петри
Тип	Правильный 7-многогранник
Семья	симплекс
Символ Шлефли	{3,3,3,3,3,3}
Диаграмма Кокстера-Динкина
6-гранный	8 6-симплекс
5-гранный	28 5-симплекс
4-ликий	56 5-клеточный
Клетки	70 тетраэдр
Лица	56 треугольник
Края	28
Вершины	8
Вершинная фигура	6-симплекс
Полигон Петри	восьмиугольник
Группа Коксетера	A ₇ [3,3,3,3,3,3]
Двойной	Самодвойственный
Характеристики	выпуклый

В 7-мерной геометрии 7- симплекс — это самодвойственный правильный 7-многогранник . Он имеет 8 вершин , 28 ребер треугольников , 56 граней , 70 тетраэдрических ячеек , 56 5-клеточных 5-граней, 28 5-симплексных 6-граней и 8 6-симплексных 7-граней. Его двугранный угол равен cos ⁻¹(1/7), или примерно 81,79°.

Альтернативные названия [ править ]

Его также можно назвать октаэксоном или окта-7-топом , как 8- гранный многогранник в 7-мерном пространстве. Название , октаексон происходит от Octa, обозначающего восемь граней греческого слова , и -ex обозначающего шестимерные грани, и -on . Джонатан Бауэрс дает октаексону аббревиатуру oca . ^[1]

В качестве конфигурации [ править ]

Эта матрица конфигурации представляет 7-симплекс. Строки и столбцы соответствуют вершинам, ребрам, граням, ячейкам, 4-граням, 5-граням и 6-граням. Диагональные числа показывают, сколько каждого элемента встречается во всем 7-симплексе. Недиагональные числа показывают, сколько элементов столбца встречается в элементе строки или рядом с ним. Матрица этого самодвойственного симплекса идентична его повороту на 180 градусов. ^[2]^[3]

${\begin{bmatrix}{\begin{matrix}8&7&21&35&35&21&7\\2&28&6&15&20&15&6\\3&3&56&5&10&10&5\\4&6&4&70&4&6&4\\5&10&10&5&56&3&3\\6&15&20&15&6&28&2\\7&21&35&35&21&7&8\end{matrix}}\end{bmatrix}}$

Симметрия [ править ]

7-симплекс как соединение двух ортогональных тетраэдров в симметричном двумерном орфографическом проекте: 2⋅{3,3} или {3,3}∨{3,3}, 6 красных ребер, 6 синих ребер и 16 желтых поперечных ребер. .	7-симплекс как объединение 4 ортогональных сегментов, спроецированных в трехмерный куб: 4⋅{ } = { }∨{ }∨{ }∨{ }. 28 ребер показаны как 12 желтых ребер куба, 12 диагоналей граней куба светло-зеленого цвета и 4 полных диагонали красного цвета. Эту перегородку можно считать тетрадисфеноидом или соединением двух дисфеноидов .

Существует множество конструкций 7-симплекса с более низкой симметрией.

Некоторые из них выражаются в виде разделов соединения двух или более нижних симплексов. Порядок симметрии каждого соединения является произведением порядка симметрии элементов и увеличивается еще больше, если идентичные элементы можно менять местами.

Присоединиться	Символ	Симметрия	Заказ	Расширенные f-векторы (факторизация)
Обычный 7-симплекс	{3,3,3,3,3,3}	[3,3,3,3,3,3]	8! = 40320	( 1 ,8,28,56,70,56,28,8, 1 )
6-симплексное соединение точек (пирамида)	{3,3,3,3,3}∨( )	[3,3,3,3,3,1]	7!×1! = 5040	( 1 ,7,21,35,35,21,7, 1 )*( 1 , 1 )
5-симплексное сегментное соединение	{3,3,3,3}∨{ }	[3,3,3,3,2,1]	6!×2! = 1440	( 1 ,6,15,20,15,6, 1 )*( 1 ,2, 1 )
5-ячеечное соединение треугольника	{3,3,3}∨{3}	[3,3,3,2,3,1]	5!×3! = 720	( 1 ,5,10,10,5, 1 )*( 1 ,3,3, 1 )
Соединение треугольник-треугольник-сегмент	{3}∨{3}∨{ }	[[3,2,3],2,1,1]	((3!) ²×2!)×2! = 144	( 1 ,3,3, 1 ) ²*( 1 ,2, 1 )
Тетраэдр - соединение тетраэдра	2⋅{3,3} = {3,3}∨{3,3}	[[3,3,2,3,3],1]	(4!) ²×2! = 1052	( 1 ,4,6,4, 1 ) ²
4-сегментное соединение	4⋅{ } = { }∨{ }∨{ }∨{ }	[4[2,2,2],1,1,1]	(2!) ⁴×4! = 384	( 1 ,2, 1 ) ⁴
соединение по 8 точкам	8⋅( )	[8[1,1,1,1,1,1]]	(1!) ⁸×8! = 40320	( 1 , 1 ) ⁸

Координаты [ править ]

Декартовы координаты вершин правильного октаэксона с центром в начале координат и длиной ребра 2:

\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ {\sqrt {1/3}},\ \pm 1\right)

\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ -2{\sqrt {1/3}},\ 0\right)

\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ -{\sqrt {3/2}},\ 0,\ 0\right)

\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ -2{\sqrt {2/5}},\ 0,\ 0,\ 0\right)

\left({\sqrt {1/28}},\ {\sqrt {1/21}},\ -{\sqrt {5/3}},\ 0,\ 0,\ 0,\ 0\right)

\left({\sqrt {1/28}},\ -{\sqrt {12/7}},\ 0,\ 0,\ 0,\ 0,\ 0\right)

\left(-{\sqrt {7/4}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)

Проще говоря, вершины 7-симплекса можно расположить в 8-мерном пространстве как перестановки (0,0,0,0,0,0,0,1). Эта конструкция основана на гранях ортоплекса 8- .

Изображения [ править ]

7-Симплекс в 3D
Модель шара и стержня в триакиса тетраэдрической оболочке	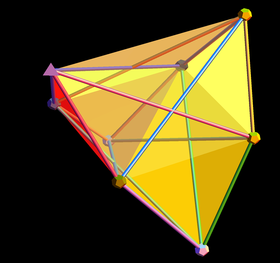7-симплекс как амплитуэдра поверхность	От 7-симплексного к 3D с перспективой камеры, показывающей намеки на 2D-проекцию Петри.

Орфографические проекции [ править ]

орфографические проекции
АК _{Коксетера} Самолет	A ₇	А ₆	A_А5
График
Двугранная симметрия	[8]	[7]	[6]
А.К.Коксетера План	A ₄	A_А3	A_А2
График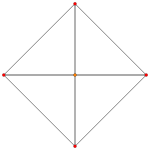
Двугранная симметрия	[5]	[4]	[3]

Связанные многогранники [ править ]

Этот многогранник является гранью однородной мозаики 3 ₃₁ с диаграммой Кокстера-Динкина :

Этот многогранник является одним из 71 однородных 7-многогранников с симметрией A ₇ .

Многогранники А7
t₀	t₁	t₂	t₃	t_0,1	t_0,2	t_1,2	t_0,3
t_1,3	t_2,3	t_0,4	t_1,4	t_2,4	t_0,5	t_1,5	t_0,6
t_0,1,2	t_0,1,3	t_0,2,3	t_1,2,3	t_0,1,4	t_0,2,4	t_1,2,4	t_0,3,4
t_1,3,4	t_2,3,4	t_0,1,5	t_0,2,5	t_1,2,5	t_0,3,5	t_1,3,5	t_0,4,5
t_0,1,6	t_0,2,6	t_0,3,6	t_0,1,2,3	t_0,1,2,4	t_0,1,3,4	t_0,2,3,4	t_1,2,3,4
t_0,1,2,5	t_0,1,3,5	t_0,2,3,5	t_1,2,3,5	t_0,1,4,5	t_0,2,4,5	t_1,2,4,5	t_0,3,4,5
t_0,1,2,6	t_0,1,3,6	t_0,2,3,6	t_0,1,4,6	t_0,2,4,6	t_0,1,5,6	t_0,1,2,3,4	t_0,1,2,3,5
t_0,1,2,4,5	t_0,1,3,4,5	t_0,2,3,4,5	t_1,2,3,4,5	t_0,1,2,3,6	t_0,1,2,4,6	t_0,1,3,4,6	t_0,2,3,4,6
t_0,1,2,5,6	t_0,1,3,5,6	t_0,1,2,3,4,5	t_0,1,2,3,4,6	t_0,1,2,3,5,6	t_0,1,2,4,5,6	t_{0,1,2,3,4,5,6}

Примечания [ править ]

^ Клитцинг, Ричард. «7D однородные многогранники (polyexa) x3o3o3o3o3o3o — oca» .
^ Коксетер, HSM (1973). «§1.8 Конфигурации». Правильные многогранники (3-е изд.). Дувр. ISBN 0-486-61480-8 .
^ Коксетер, HSM (1991). Правильные комплексные многогранники (2-е изд.). Издательство Кембриджского университета. п. 117. ИСБН 9780521394901 .

Внешние ссылки [ править ]

Глоссарий по гиперпространству , Георгий Ольшевский.
Многогранники различных размерностей
Многомерный глоссарий

v т и Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
Семья	н	Б _н	И ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ж ₄ / Г ₂	Ч _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16 ячеек • Тессеракт	Демитессеракт	24-ячеечный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Равномерный n - многогранник	n - симплекс	n - ортоплекс • n - куб	n - демикуб	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.

[1] Клитцинг, Ричард. «7D однородные многогранники (polyexa) x3o3o3o3o3o3o — oca» .

[2] Коксетер, HSM (1973). «§1.8 Конфигурации». Правильные многогранники (3-е изд.). Дувр. ISBN 0-486-61480-8 .

[3] Коксетер, HSM (1991). Правильные комплексные многогранники (2-е изд.). Издательство Кембриджского университета. п. 117. ИСБН 9780521394901 .

[1]

[2]

[3]