Шестигранные 7-симплексы
 7-симплекс | 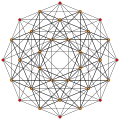 Шестигранный 7-симплекс |  Шестиусеченный 7-симплекс |  Шестикантеллярный 7-симплекс |
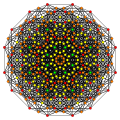 Шестиструнный 7-симплекс |  Гексикантиусеченный 7-симплекс |  Шестиусеченный 7-симплекс |  Шестигранникантеллированный 7-симплекс |
 Гексистериусеченный 7-симплекс |  Гексистерикантеллированный 7-симплекс |  Гексипентиусеченный 7-симплекс |  Шестигранно-усеченный 7-симплекс |
 Гексистерический усеченный 7-симплекс |  Гексистерирундусеченный 7-симплекс |  Гексистерирунчикантеллированный 7-симплекс |  Гексипентикантитусеченный 7-симплекс |
 Шестипериусеченный 7-симплекс | 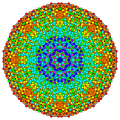 Гексистерирунсикантиусеченный 7-симплекс |  Гексипентирунсикантиусеченный 7-симплекс |  Гексипентистерикантиусеченный 7-симплекс |
 Гексипентистерирунцикантиусеченный 7-симплекс (Всеусеченный 7-симплекс) | |||
| Ортогональные проекции в A 7. плоскости Кокстера | |||
|---|---|---|---|
В семимерной геометрии гексикированный 7-симплекс — это выпуклый однородный 7-многогранник , включая усечения 6-го порядка (гексикация) от правильного 7-симплекса .
Для 7-симплекса существует 20 уникальных гексикаций, включая все перестановки усечений, кантелляций, рансинаций, стерикаций и пентелляций.
Простой шестигранный 7-симплекс также называется расширенным 7-симплексом , в котором только первый и последний узлы окольцованы, и создается с помощью операции расширения, примененной к обычному 7-симплексу . Высшую форму, гексипентистерирунсицантитусеченный 7-симплекс , проще назвать омниусеченным 7-симплексом со всеми узлами, окольцованными.
Шестигранный 7-симплекс
[ редактировать ]| Шестигранный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | 254: 8+8 {3 5 } 28+28 {}x{3 4 } 56+56 {3}х{3,3,3} 70 {3,3}х{3,3} |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 336 |
| Вершины | 56 |
| Вершинная фигура | 5-симплексная антипризма |
| Группа Коксетера | A 7 ×2, [[3 6 ]], заказ 80640 |
| Характеристики | выпуклый |
В семимерной геометрии шестигранный 7-симплекс представляет собой выпуклый однородный 7-многогранник , гексакцию (усечение 6-го порядка) регулярного 7-симплекса или, альтернативно, можно рассматривать как операцию расширения .

Корневые векторы
[ редактировать ]Его 56 вершин представляют корневые векторы простой группы Ли A 7 .
Альтернативные названия
[ редактировать ]- Расширенный 7-симплекс
- Маленький петированный гексадекаексон (аббревиатура: suph) (Джонатан Бауэрс) [1]
Координаты
[ редактировать ]Вершины шестигранного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,1,1,1,1,2). Эта конструкция основана на гранях шестигранного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Вторая конструкция в 8-мерном пространстве из центра выпрямленного 8-ортоплекса задается координатными перестановками:
- (1,-1,0,0,0,0,0,0)
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График | 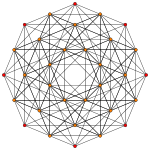 |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Шестиусеченный 7-симплекс
[ редактировать ]| шестиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 1848 |
| Вершины | 336 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петитусеченный октаексон (аббревиатура: путо) (Джонатан Бауэрс) [2]
Координаты
[ редактировать ]Вершины шестиусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,1,1,1,2,3). Эта конструкция основана на гранях шестиусеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График | 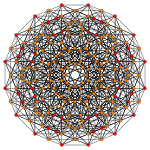 |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Шестикантеллярный 7-симплекс
[ редактировать ]| Шестикантеллярный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,2,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 5880 |
| Вершины | 840 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петиромбатированный октаэксон (аббревиатура: пуро) (Джонатан Бауэрс) [3]
Координаты
[ редактировать ]Вершины шестикантеллированного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,1,1,2,2,3). Эта конструкция основана на гранях шестикантеллярного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Шестиструнный 7-симплекс
[ редактировать ]| Шестиструнный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,3,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 8400 |
| Вершины | 1120 |
| Вершинная фигура | |
| Группа Коксетера | A 7 ×2, [[3 6 ]], заказ 80640 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петипризматический гексадекаексон (аббревиатура: puph) (Джонатан Бауэрс) [4]
Координаты
[ редактировать ]Вершины шестиструнного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,1,2,2,2,3). Эта конструкция основана на гранях шестиспиралевидного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  | 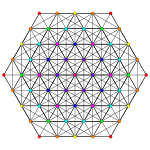 |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Гексикантиусеченный 7-симплекс
[ редактировать ]| Гексикантиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 8400 |
| Вершины | 1680 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петигреаторомбатированный октаэксон (аббревиатура: пугро) (Джонатан Бауэрс) [5]
Координаты
[ редактировать ]Вершины гексикантиусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,1,1,2,3,4). Эта конструкция основана на гранях гексикантиусеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Шестиусеченный 7-симплекс
[ редактировать ]| Шестиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,3,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 20160 |
| Вершины | 3360 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петипризматоусеченный октаексон (аббревиатура: pupato) (Джонатан Бауэрс) [6]
Координаты
[ редактировать ]Вершины шестиусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,1,2,2,3,4). Эта конструкция основана на гранях шестиусеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Шестигранникантеллированный 7-симплекс
[ редактировать ]| Шестигранникантеллированный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,2,3,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 16800 |
| Вершины | 3360 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
В семимерной геометрии шестисвеченный 7-симплекс представляет собой однородный 7-многогранник .
Альтернативные названия
[ редактировать ]- Петипризматоромбатированный октаэксон (аббревиатура: пупро) (Джонатан Бауэрс) [7]
Координаты
[ редактировать ]Вершины шестиграннокантеллированного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,1,2,3,3,4). Эта конструкция основана на гранях шестиграннокантеллированного 8-ортоплекса . ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Гексистериусеченный 7-симплекс
[ редактировать ]| гексистеритусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,4,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 20160 |
| Вершины | 3360 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петицеллитусеченный октаэксон (аббревиатура: пукто) (Джонатан Бауэрс) [8]
Координаты
[ редактировать ]Вершины гексистериусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,2,2,2,3,4). Эта конструкция основана на гранях гексистериусеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Гексистерикантеллированный 7-симплекс
[ редактировать ]| шестистериконтеллярный 7-симплексный | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,2,4,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | т 0,2,4 {3,3,3,3,3} {}хт 0,2,4 {3,3,3,3} |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 30240 |
| Вершины | 5040 |
| Вершинная фигура | |
| Группа Коксетера | A 7 ×2, [[3 6 ]], заказ 80640 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петицеллиромбигексадекаексон (аббревиатура: пукрох) (Джонатан Бауэрс) [9]
Координаты
[ редактировать ]Вершины шестистерикантеллированного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,2,2,3,3,4). Эта конструкция основана на гранях гексистерикантеллированного 8-ортоплекса . ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Гексипентиусеченный 7-симплекс
[ редактировать ]| Гексипентиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,5,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 8400 |
| Вершины | 1680 |
| Вершинная фигура | |
| Группа Коксетера | A 7 ×2, [[3 6 ]], заказ 80640 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петитертусеченный гексадекаексон (аббревиатура: путат) (Джонатан Бауэрс) [10]
Координаты
[ редактировать ]Вершины шестипентитусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,2,2,2,2,3,4). Эта конструкция основана на гранях шестипентитусеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Шестигранно-усеченный 7-симплекс
[ редактировать ]| Шестигранно-усеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,3,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 30240 |
| Вершины | 6720 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петигреатопризматический октаэксон (аббревиатура: пугопо) (Джонатан Бауэрс) [11]
Координаты
[ редактировать ]Вершины шестигранно-усеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,2,2,3,4,5). Эта конструкция основана на гранях шестиспиралевидноусеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Гексистерический усеченный 7-симплекс
[ редактировать ]| Гексистерический усеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,4,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 50400 |
| Вершины | 10080 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петичеллигреаторомбатированный октаэксон (аббревиатура: пукагро) (Джонатан Бауэрс) [12]
Координаты
[ редактировать ]Вершины гексистерически-усеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,2,2,3,4,5). Эта конструкция основана на гранях гексистерического -усеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Гексистерирундусеченный 7-симплекс
[ редактировать ]| Гексистерирундусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,3,4,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 45360 |
| Вершины | 10080 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петицеллипризматоусеченный октаэксон (аббревиатура: pucpato) (Джонатан Бауэрс) [13]
Координаты
[ редактировать ]Вершины шестигранно-усеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,2,3,3,4,5). Эта конструкция основана на гранях гексистерически- усеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График | 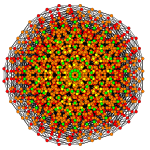 |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Гексистерирунчикантеллированный 7-симплекс
[ редактировать ]| Гексистерирунчикантеллированный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,2,3,4,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 45360 |
| Вершины | 10080 |
| Вершинная фигура | |
| Группа Коксетера | A 7 ×2, [[3 6 ]], заказ 80640 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петицеллипризматоромбигексадекаэксон (аббревиатура: pucproh) (Джонатан Бауэрс) [14]
Координаты
[ редактировать ]Вершины шестигранно-усеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,2,3,4,4,5). Эта конструкция основана на гранях гексистерически- усеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Гексипентикантитусеченный 7-симплекс
[ редактировать ]| гексипентикантитусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,5,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 30240 |
| Вершины | 6720 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Petiterigreatorhombated октаэксон (аббревиатура: putagro) (Джонатан Бауэрс) [15]
Координаты
[ редактировать ]Вершины гексипентикантитусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,2,2,2,3,4,5). Эта конструкция основана на гранях гексипентикантиусеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Шестипериусеченный 7-симплекс
[ редактировать ]| Шестипериусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,3,5,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | |
| Вершины | 10080 |
| Вершинная фигура | |
| Группа Коксетера | A 7 ×2, [[3 6 ]], заказ 80640 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Petiteriprismatoусеченный гексадекаэксон (аббревиатура: putpath) (Джонатан Бауэрс) [16]
Координаты
[ редактировать ]Вершины шестипериусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,2,2,3,4,4,5). Эта конструкция основана на гранях шестиперикрученного усеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Гексистерирунсикантиусеченный 7-симплекс
[ редактировать ]| Гексистерирунсикантиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,3,4,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 80640 |
| Вершины | 20160 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петигреатоцеллированный октаэксон (аббревиатура: pugaco) (Джонатан Бауэрс) [17]
Координаты
[ редактировать ]Вершины шестигранного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,1,2,3,4,5,6). Эта конструкция основана на гранях гексистерирунсикантиусеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График | 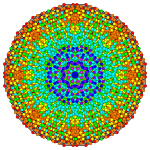 |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Гексипентирунсикантиусеченный 7-симплекс
[ редактировать ]| Гексипентирунсикантиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,3,5,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 80640 |
| Вершины | 20160 |
| Вершинная фигура | |
| Группа Коксетера | A 7 , [3 6 ], заказ 40320 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Петеригреатопризматический октаексон (аббревиатура: путгапо) (Джонатан Бауэрс) [18]
Координаты
[ редактировать ]Вершины шестигранно-усеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,2,2,3,4,5,6). Эта конструкция основана на гранях гексипентирунсикантиусеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Гексипентистерикантиусеченный 7-симплекс
[ редактировать ]| Гексипентистерикантиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,4,5,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 80640 |
| Вершины | 20160 |
| Вершинная фигура | |
| Группа Коксетера | A 7 ×2, [[3 6 ]], заказ 80640 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Petitericelligreatorhombihexadecaexon (аббревиатура: putcagroh) (Джонатан Бауэрс) [19]
Координаты
[ редактировать ]Вершины гексипентистерикоантитусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,2,3,3,4,5,6). Эта конструкция основана на гранях гексипентистерикоантитусеченного 8-ортоплекса , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Всеусеченный 7-симплекс
[ редактировать ]| Всеусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,3,4,5,6 {3 6 } |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | 254 |
| 5-гранный | 5796 |
| 4-ликий | 40824 |
| Клетки | 126000 |
| Лица | 191520 |
| Края | 141120 |
| Вершины | 40320 |
| Вершинная фигура | Ирр. 6-симплекс |
| Группа Коксетера | A 7 ×2, [[3 6 ]], заказ 80640 |
| Характеристики | выпуклый |
Всеусеченный 7-симплекс состоит из 40320 (8 факториалов ) вершин и является крупнейшим однородным 7-многогранником в симметрии A 7 обычного 7-симплекса. Его также можно назвать гексипентистерирунцикантиусеченным 7-симплексом , что является длинным названием омнитуркеции для 7 измерений со всеми активными отражающими зеркалами.
Пермутоэдр и связанная с ним мозаика
[ редактировать ]Омниусеченный 7-симплекс — это пермутоэдр 8-го порядка. Омниусеченный 7-симплекс — это зонотоп , сумма Минковского восьми отрезков, параллельных восьми прямым, проходящим через начало координат, и восьми вершинам 7-симплекса.
Как и все однородные всеусеченные n-симплексы, всеусеченный 7-симплекс может мозаично представлять собой сам по себе пространство, в данном случае 7-мерное пространство с тремя гранями вокруг каждого гребня . Имеется Кокстера-Динкина . диаграмма ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Альтернативные названия
[ редактировать ]- Большой петированный гексадекаексон (аббревиатура: гуф) (Джонатан Бауэрс) [20]
Координаты
[ редактировать ]Вершины всеусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,1,2,3,4,5,6,7). Эта конструкция основана на гранях гексипентистерирунсикантиусеченного 8-ортоплекса , t 0,1,2,3,4,5,6 {3 6 ,4}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Связанные многогранники
[ редактировать ]Эти многогранники являются частью 71 однородного 7-многогранника с симметрией A 7 .
| Многогранники А7 |
|---|
Примечания
[ редактировать ]- ^ Клитцинг, (x3o3o3o3o3o3x - супф)
- ^ Клитцинг, (x3x3o3o3o3o3x-puto)
- ^ Клитцинг, (x3o3x3o3o3o3x - пуро)
- ^ Клитцинг, (x3o3o3x3o3o3x - пуф)
- ^ Клитцинг, (x3o3o3o3x3o3x - пугро)
- ^ Клитцинг, (x3x3x3o3o3o3x - куколка)
- ^ Клитцинг, (x3o3x3x3o3o3x - пупро)
- ^ Клитцинг, (x3x3o3o3x3o3x - пукто)
- ^ Клитцинг, (x3o3x3o3x3o3x - пукрох)
- ^ Клитцинг, (x3x3o3o3o3x3x - путат)
- ^ Клитцинг, (x3x3x3x3o3o3x - пугопо)
- ^ Клитцинг, (x3x3x3o3x3o3x - пукагро)
- ^ Клитцинг, (x3x3o3x3x3o3x - pucpato)
- ^ Клитцинг, (x3o3x3x3x3o3x - pucproh)
- ^ Клитцинг, (x3x3x3o3o3x3x - putagro)
- ^ Клитцинг, (x3x3o3x3o3x3x - путь пути)
- ^ Клитцинг, (x3x3x3x3x3o3x - пугако)
- ^ Клитцинг, (x3x3x3x3o3x3x - путгапо)
- ^ Клитцинг, (x3x3x3o3x3x3x - putcagroh)
- ^ Клитцинг, (x3x3x3x3x3x3x - гаф)
Ссылки
[ редактировать ]- ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 , Wiley.com
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии (1966)
- Клитцинг, Ричард. «7Д» . х3о3о3о3о3о3х - супх, х3х3о3о3о3о3х- путо, х3о3х3о3о3о3х - пуро, х3о3о3х3о3о3х - пуф, х3о3о3о3х3о3х - пугро, х3х3х3о3о3о3х - куколка, х3х3о3о3х3о3х - пукто, x3o3x3o3x3o3x - пукрох, x3x3o3o3o3x3x - путат, x3x3x3x3o3o3x - пугопо, x3x3x3o3x3o3x - пукагро, x3x3o3x3x3o3x - pucpato, x3o3x3x3x3o3x - pucproh, x3x3x3o3o3x3x - putagro, x3x3x3x3o3x3x - putpath, x3x3x3x3x3o3x - pugaco, x3x3x3x3o3x3x - putgapo, x3x3x3o3x3x3x - putcagroh, x3x3x3x3x 3x3x - guph






































































