Пятеричные 7-симплексы
 7-симплекс |  Пятеричный 7-симплекс |  Пятиусеченный 7-симплекс |  Пятиконтеллярный 7-симплекс |
 Пентикантиусеченный 7-симплекс |  Пятислойный 7-симплекс |  Пятикруглый усеченный 7-симплекс |  Пятирунчикантеллированный 7-симплекс |
 Пентирунсикантиусеченный 7-симплекс |  Пентистерифицированный 7-симплекс |  Пентистеритусеченный 7-симплекс |  Пентистерикантеллированный 7-симплекс |
 Пентистерикантиусеченный 7-симплекс |  Пентистерирцинтированный 7-симплекс |  Пентистерирундусеченный 7-симплекс |  Пентистерирунцикантеллярный 7-симплекс |
 Пентистерирунцикантиусеченный 7-симплекс | |||
В семимерной геометрии пятимерный 7-симплекс — это выпуклый однородный 7-многогранник с усечениями ( пентелляцией ) 5-го порядка правильного 7-симплекса .
Существует 16 уникальных пентелляций 7-симплекса с перестановками усечений, кантелляций, рансинаций и стерикаций.
Пятеричный 7-симплекс
[ редактировать ]| Пятеричный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 1260 |
| Вершины | 168 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Малый терированный октаэксон (аббревиатура: сето) (Джонатан Бауэрс) [1]
Координаты
[ редактировать ]Вершины пятиугольного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,1,1,1,1,2). Эта конструкция основана на гранях пятиугольного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пятиусеченный 7-симплекс
[ редактировать ]| пятиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 5460 |
| Вершины | 840 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Теритусеченный октаэксон (аббревиатура: тето) (Джонатан Бауэрс) [2]
Координаты
[ редактировать ]Вершины пятиусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,1,1,1,2,3). Эта конструкция основана на гранях пятиусеченного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пятиконтеллярный 7-симплекс
[ редактировать ]| Пятиконтеллярный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,2,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 11760 |
| Вершины | 1680 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Териромбированный октаэксон (аббревиатура: теро) (Джонатан Бауэрс) [3]
Координаты
[ редактировать ]Вершины пятизубчатого 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,1,1,2,2,3). Эта конструкция основана на гранях пятизубчатого 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пентикантиусеченный 7-симплекс
[ редактировать ]| пентикантиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | |
| Вершины | |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Теригреаторомбатированный октаэксон (аббревиатура: тегро) (Джонатан Бауэрс) [4]
Координаты
[ редактировать ]Вершины пятиантиусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,1,1,2,3,4). Эта конструкция основана на гранях пентикантиусеченного 8-ортоплекса .
| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  | 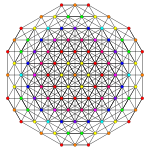 |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пятислойный 7-симплекс
[ редактировать ]| пятиструнный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,3,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 10920 |
| Вершины | 1680 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Терипризматический октаэксон (аббревиатура: тепо) (Джонатан Бауэрс) [5]
Координаты
[ редактировать ]Вершины пятистержневого 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,1,2,2,2,3). Эта конструкция основана на гранях пятистержневого 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пятикруглый усеченный 7-симплекс
[ редактировать ]| пятиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,3,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 27720 |
| Вершины | 5040 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Териприсматоусеченный октаэксон (аббревиатура: тапто) (Джонатан Бауэрс) [6]
Координаты
[ редактировать ]Вершины пятиусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,1,2,2,3,4). Эта конструкция основана на гранях пятиусеченного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пятирунчикантеллированный 7-симплекс
[ редактировать ]| пятигранный 7-симплексный | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,2,3,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 25200 |
| Вершины | 5040 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Терипризматоромбатированный октаэксон (аббревиатура: тапро) (Джонатан Бауэрс) [7]
Координаты
[ редактировать ]Вершины пятиграннокантеллированного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,1,2,3,3,4). Эта конструкция основана на гранях пятигранно- пятнистого 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пентирунсикантиусеченный 7-симплекс
[ редактировать ]| пятигранныйусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,3,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 45360 |
| Вершины | 10080 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Теригреатопризматический октаэксон (аббревиатура: тегапо) (Джонатан Бауэрс) [8]
Координаты
[ редактировать ]Вершины пятиусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,1,2,3,4,5). Эта конструкция основана на гранях пятиусеченного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пентистерифицированный 7-симплекс
[ редактировать ]| пентистеризованный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,4,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 4200 |
| Вершины | 840 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Терицеллярный октаэксон (аббревиатура: теко) (Джонатан Бауэрс) [9]
Координаты
[ редактировать ]Вершины пентистеризованного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,0,1,2,2,2,3). Эта конструкция основана на гранях пентистеризованного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  | 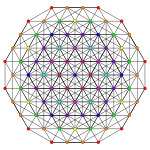 |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пентистеритусеченный 7-симплекс
[ редактировать ]| пентистеритусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,4,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 15120 |
| Вершины | 3360 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Терицеллитусеченный октаэксон (аббревиатура: текто) (Джонатан Бауэрс) [10]
Координаты
[ редактировать ]Вершины пентистеритусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,2,2,3,4,4). Эта конструкция основана на гранях пентистеритусеченного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пентистерикантеллированный 7-симплекс
[ редактировать ]| пентистерикантеллированный, 7-симплексный | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,2,4,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 25200 |
| Вершины | 5040 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Терицеллиромбированный октаэксон (аббревиатура: текро) (Джонатан Бауэрс) [11]
Координаты
[ редактировать ]Вершины пентистерикантеллированного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,2,2,3,3,4). Эта конструкция основана на гранях пентистерикантеллированного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пентистерикантиусеченный 7-симплекс
[ редактировать ]| пентистерикантиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,4,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 40320 |
| Вершины | 10080 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Tericelligreatorhombated октаэксон (аббревиатура: tecagro) (Джонатан Бауэрс) [12]
Координаты
[ редактировать ]Вершины пентистерико-усеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,2,2,3,4,5). Эта конструкция основана на гранях пентистерикантитусеченного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пентистерирцинтированный 7-симплекс
[ редактировать ]| Пентистерирцинтированный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,3,4,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 15120 |
| Вершины | 3360 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Бипентикантиусеченный 7-симплекс как t 1,2,3,6 {3,3,3,3,3,3}
- Терицеллипризматический октаэксон (аббревиатура: tacpo) (Джонатан Бауэрс) [13]
Координаты
[ редактировать ]Вершины пентистерекулярного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,2,3,3,3,4). Эта конструкция основана на гранях пентистерекулярного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [7] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [5] | [4] | [3] |
Пентистерирундусеченный 7-симплекс
[ редактировать ]| пентистерирундусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,3,4,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 40320 |
| Вершины | 10080 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Терицеллипризматоусеченный октаэксон (аббревиатура: tacpeto) (Джонатан Бауэрс) [14]
Координаты
[ редактировать ]Вершины пентистериро-усеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,2,3,3,4,5). Эта конструкция основана на гранях пентистериро -усеченного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Пентистерирунцикантеллярный 7-симплекс
[ редактировать ]| пентистерирунчикантеллированный, 7-симплексный | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,2,3,4,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 40320 |
| Вершины | 10080 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Бипентирунцикантиусеченный 7-симплекс как т 1,2,3,4,6 {3,3,3,3,3,3}
- Терицеллипризматоромбатированный октаэксон (аббревиатура: tacpro) (Джонатан Бауэрс) [15]
Координаты
[ редактировать ]Вершины пентистерирунцикантеллированного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,2,3,4,4,5). Эта конструкция основана на гранях пентистерирунцикантеллярного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Пентистерирунцикантиусеченный 7-симплекс
[ редактировать ]| пентистерирунсикантиусеченный 7-симплекс | |
|---|---|
| Тип | однородный 7-многогранник |
| Символ Шлефли | т 0,1,2,3,4,5 {3,3,3,3,3,3} |
| Диаграммы Кокстера-Динкина | |
| 6-гранный | |
| 5-гранный | |
| 4-ликий | |
| Клетки | |
| Лица | |
| Края | 70560 |
| Вершины | 20160 |
| Вершинная фигура | |
| Группы Кокстера | A 7 , [3,3,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Большой терированный октаэксон (аббревиатура: гето) (Джонатан Бауэрс) [16]
Координаты
[ редактировать ]Вершины пентистерирунсикантиусеченного 7-симплекса проще всего расположить в 8-мерном пространстве как перестановки (0,0,1,2,3,4,5,6). Эта конструкция основана на гранях пентистерирунцикантиусеченного 8-ортоплекса .
Изображения
[ редактировать ]| АК Коксетера Самолет | A 7 | А 6 | AА5 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [[7]] | [6] |
| А.К.Коксетера План | A 4 | AА3 | AА2 |
| График |  |  |  |
| Двугранная симметрия | [[5]] | [4] | [[3]] |
Связанные многогранники
[ редактировать ]Эти многогранники являются частью набора из 71 однородного 7-многогранника с симметрией A 7 .
| Многогранники А7 |
|---|
Примечания
[ редактировать ]- ^ Клитцинг, (x3o3o3o3o3x3o - сето)
- ^ Клитцинг, (x3x3o3o3o3x3o - тето)
- ^ Клитцинг, (x3o3x3o3o3x3o - теро)
- ^ Клитцинг, (x3x3x3oxo3x3o - тегро)
- ^ Клитцинг, (x3o3o3x3o3x3o - тепо)
- ^ Клитцинг, (x3x3o3x3o3x3o - тапто)
- ^ Клитцинг, (x3o3x3x3o3x3o - тапро)
- ^ Клитцинг, (x3x3x3x3o3x3o - тегапо)
- ^ Клитцинг, (x3o3o3o3x3x3o - теко)
- ^ Клитцинг, (x3x3o3o3x3x3o - текто)
- ^ Клитцинг, (x3o3x3o3x3x3o - текро)
- ^ Клитцинг, (x3x3x3o3x3x3o - tecagro)
- ^ Клитцинг, (x3o3o3x3x3x3o - такпо)
- ^ Клитцинг, (x3x3o3x3x3x3o - такпето)
- ^ Клитцинг, (x3o3x3x3x3x3o - tacpro)
- ^ Клитцинг, (x3x3x3x3x3x3o - получить)
Ссылки
[ редактировать ]- ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
- Клитцинг, Ричард. «7D однородные многогранники (полиекса)» . х3о3о3о3о3х3о - сето, х3х3о3о3о3х3о - тето, х3о3х3о3о3х3о - теро, х3х3х3оксо3х3о - тегро, х3о3о3х3о3х3о - тепо, х3х3о3х3о3х3о - тапто, х3о3х3х3о3х3о - тапро, х 3х3х3х3о3х3о - тегапо, х3о3о3о3х3х3о - теко, х3х3о3о3х3х3о - текто, х3о3х3о3х3х3о - текро, х3х3х3о3х3х3о - текагро, х3о3о3х3х3х3о - tacpo, x3x3o3x3x3x3o - tacpeto, x3o3x3x3x3x3o - tacpro, x3x3x3x3x3x3o - geto






































































