9-куб
Эта статья включает список литературы , связанную литературу или внешние ссылки , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . ( сентябрь 2017 г. ) |
| 9-куб Эннеракт | |
|---|---|
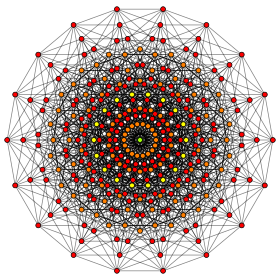 Ортогональная проекция внутри многоугольника Петри Оранжевые вершины удвоены, желтые — 4, а зеленый центр — 8. | |
| Тип | Правильный 9-многогранник |
| Семья | гиперкуб |
| Символ Шлефли | {4,3 7 } |
| Диаграмма Кокстера-Динкина | |
| 8-гранный | 18 {4,3 6 } |
| 7-гранный | 144 {4,3 5 } |
| 6-гранный | 672 {4,3 4 } |
| 5-гранный | 2016 {4,3 3 } |
| 4-ликий | 4032 {4,3,3} |
| Клетки | 5376 {4,3} |
| Лица | 4608 {4} |
| Края | 2304 |
| Вершины | 512 |
| Вершинная фигура | 8-симплекс |
| Полигон Петри | восьмиугольник |
| Группа Коксетера | С 9 , [3 7 ,4] |
| Двойной | 9-ортоплекс |
| Характеристики | выпуклый многогранник Ханнера |
В геометрии 9 -куб — это девятимерный гиперкуб с 512 вершинами , 2304 ребрами , 4608 квадратными гранями , 5376 кубическими ячейками , 4032 тессерактом с 4 гранями , 2016 5-кубом с 5 гранями , 672 6-кубами с 6 гранями , 144 7-кубов с 7 гранями и 18 8-кубов с 8 гранями .
Его можно назвать по символу Шлефли {4,3 7 }, состоящего из трёх восьмёрок вокруг каждой 7-грани. Его также называют эннерактом , сумкой из тессеракта ( четырехкуба ) и энне, обозначающего девять (измерений) на греческом языке . Его также можно назвать правильным октадека-9-топом или октадекайоттоном , как девятимерный многогранник, построенный с 18 правильными гранями .
Он является частью бесконечного семейства многогранников, называемых гиперкубами. Двойственный 9-кубу можно назвать 9-ортоплексом и является частью бесконечного семейства перекрестных многогранников .
Декартовы координаты [ править ]
Декартовы координаты вершин 9-куба с центром в начале координат и длиной ребра 2 равны
- (±1,±1,±1,±1,±1,±1,±1,±1,±1)
в то время как его внутренняя часть состоит из всех точек ( x 0 , x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 , x 8 ) с −1 < x i < 1.
Прогнозы [ править ]
 Этот граф из 9 кубов является ортогональной проекцией . Эта ориентация показывает столбцы вершин, расположенные на расстоянии вершина-ребро-вершина от одной вершины слева до одной вершины справа, а также ребра, соединяющие соседние столбцы вершин. Количество вершин в каждом столбце представляет собой строки в треугольнике Паскаля и составляет 1:9:36:84:126:126:84:36:9:1. |
Изображения [ править ]
| BБ9 | Б 8 | Б 7 | |||
|---|---|---|---|---|---|
 |  | 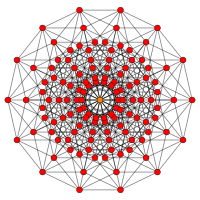 | |||
| [18] | [16] | [14] | |||
| Б 6 | Б 5 | ||||
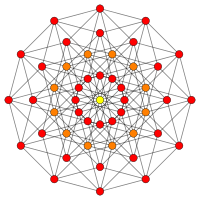 | 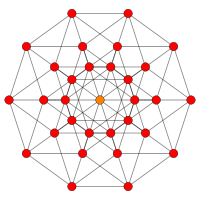 | ||||
| [12] | [10] | ||||
| Б 4 | BБ3 | BБ2 | |||
 |  |  | |||
| [8] | [6] | [4] | |||
| A 7 | AА5 | AА3 | |||
 |  |  | |||
| [8] | [6] | [4] | |||
Производные многогранники [ править ]
Применение операции чередования , удаляющей чередующиеся вершины 9-куба , создает другой однородный многогранник , называемый 9-демикубом (часть бесконечного семейства, называемого демигиперкубами ), который имеет 18 8-демикубов и 256 8-симплексных граней.
Примечания [ править ]
Ссылки [ править ]
- ХСМ Коксетер :
- Коксетер, Правильные многогранники (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 , с. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерностях (n≥5).
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973, стр. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерностях (n≥5).
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии. (1966)
- Клитцинг, Ричард. «9D однородные многогранники (полийотта) o3o3o3o3o3o3o3o4x - enne» .
Внешние ссылки [ править ]
- Вайсштейн, Эрик В. «Гиперкуб» . Математический мир .
- Ольшевский, Георгий. «Измерить многогранник» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
- Многомерный глоссарий: гиперкуб Гаррета Джонса