Чередование (геометрия)

Чередование куба создает тетраэдр .

Чередование усеченного кубооктаэдра создает неоднородный курносый куб .

В геометрии чередование или частичное усечение — это операция над многоугольником , многогранником , мозаикой или многогранником более высокой размерности , которая удаляет альтернативные вершины.

Коксетер обозначает чередование префиксом h , обозначающим полу или половину . Поскольку чередование уменьшает количество сторон всех многоугольников вдвое, его можно применять только к многогранникам со всеми четными гранями. Чередованная квадратная грань становится двуугольником и , будучи вырожденной, обычно сводится к одному ребру.

любой вершинно-однородный многогранник или мозаику с конфигурацией вершин , состоящей из всех элементов с четными номерами В более общем смысле можно чередовать . Например, чередование вершинной фигуры с 2a.2b.2c — это a.3.b.3.c.3 , где тройка — количество элементов в этой вершинной фигуре. Особый случай — квадратные грани, порядок которых делится пополам на вырожденные двуугольники . Так, например, куб 4.4.4 чередуется с 2.3.2.3.2.3 , который сокращается до 3.3.3, являясь тетраэдром , и все 6 ребер тетраэдров также можно рассматривать как вырожденные грани исходного куба.

Пренебрежение

Дополнительная информация: Курносый (геометрия).

Курносый терминологии в Коксетера ) можно рассматривать как чередование усеченного ( правильного или усеченного квазиправильного многогранника. В общем случае многогранник можно обойти, если его усечение имеет только четные грани. Все усеченные выпрямленные многогранники могут быть удалены не только из правильных многогранников.

Курносая квадратная антипризма является примером общей курносой и может быть представлена ​​как ss{2,4} с квадратной антипризмой s{2,4}.

Альтернативные многогранники

Эта операция чередования также применима к многогранникам и сотам более высокой размерности, но в целом большинство результатов этой операции не будут однородными. Пустоты, созданные удаленными вершинами, обычно не создают однородных граней, и обычно не хватает степеней свободы для соответствующего изменения масштаба новых ребер. Однако существуют исключения, такие как получение курносых 24-элементных из усеченных 24-элементных .

Примеры:

• Соты
  1. Чередованными кубическими сотами являются тетраэдрально-октаэдрические соты .
  2. Перемежающиеся шестиугольные призматические соты представляют собой вращающиеся перемежающиеся кубические соты .
• 4-многогранник
  1. Альтернативно усеченные 24 ячейки представляют собой курносые 24 ячейки .
• 4-соты:
  1. Чередованные усеченные соты из 24 ячеек представляют собой курносые соты из 24 ячеек .
• Гиперкуб полугиперкубом можно чередовать с однородным . всегда
  1. Куб → Тетраэдр (правильный)
     • →
  2. Тессеракт ( 8 ячеек ) → 16 ячеек (обычный)
     • →
  3. Пентеракт → демипентеракт (полурегулярный)
  4. Гексеракт → полугексеракт (униформа)
  5. ...

Видоизмененные многогранники

Коксетер также использовал оператор a , который содержит обе половины, поэтому сохраняет исходную симметрию. Для четносторонних правильных многогранников a{2p,q} представляет собой составной многогранник с двумя противоположными копиями h{2p,q}. Для нечетных, больше 3, правильных многогранников a{p,q} становится звездчатым многогранником .

Норман Джонсон расширил использование измененного оператора a {p,q}, b {p,q} для смешанного и c {p,q} для преобразованного , как , , и соответственно.

Составной многогранник, известный как звездчатый октаэдр, может быть представлен как {4,3} (измененный куб ), и , .

Звездчатый многогранник, известный как малый дитригональный икосододекаэдр, может быть представлен как {5,3} (измененный додекаэдр ) и , . Здесь все пятиугольники чередовались в пентаграммы, а треугольники вставлялись, чтобы занять образовавшиеся свободные края.

Звездный многогранник, известный как большой дитригональный икосододекаэдр, может быть представлен как {5/2,3} (измененный большой звездчатый додекаэдр ) и , . Здесь все пентаграммы снова превратились в пятиугольники, а образовавшиеся свободные края были вставлены в треугольники.

Альтернативные сокращения

Подобная операция может усекать альтернативные вершины, а не просто удалять их. Ниже представлен набор многогранников, которые можно сгенерировать из каталонских тел . Они имеют два типа вершин, которые можно поочередно обрезать. Усечение вершин «высшего порядка» и обоих типов вершин дает следующие формы:

Имя	Оригинал	Чередование усечение	Усечение	Сокращенное имя
Куб Двойник выпрямленного тетраэдра				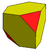Альтернативный усеченный куб
Ромбический додекаэдр Двойник кубооктаэдра		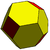		Усеченный ромбдодекаэдр
Ромбический триаконтаэдр Двойник икосододекаэдра				Усеченный ромбический триаконтаэдр
Тетраэдр Триакиса Двойник усеченного тетраэдра				Усеченный триакис тетраэдр
Октаэдр Триакиса Двойник усеченного куба				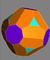Усеченный триакисоктаэдр
Триакис икосаэдр Двойник усеченного додекаэдра				Усеченный триакисикосаэдр

См. также

• Обозначение многогранников Конвея
• Строительство Витхоффа

Ссылки

• Коксетер, Правильные многогранники HSM (3-е издание, 1973 г.), Дуврское издание, ISBN   0-486-61480-8
• Нормана Джонсона Равномерные многогранники , Рукопись (1991)
  • Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
• Вайсштейн, Эрик В. «Кнобификация» . Математический мир .
• Ричард Клитцинг, Снабс, чередующиеся грани и диаграммы Стотта-Коксетера-Динкина , Симметрия: Культура и Наука, Том. 21, №4, 329-344, (2010) [1]

Внешние ссылки

• Ольшевский, Георгий. «Чередование» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
• Имена многогранников, курносые

Операторы многогранника

Семя	Усечение	Исправление	Биусечение	Двойной	Расширение	Всеобрезание	Чередования
т 0 { п , q } { п , q }	т 01 { п , q } т { п , q }	т 1 { п , q } р { п , q }	т 12 { п , q } 2t{ п , q }	т 2 { п , q } 2r{ п , q }	т 02 { п , q } рр { п , q }	т 012 { п , q } тр { п , q }	чт 0 { п , q } ч { q , п }	чт 12 { п , q } с { q , п }	чт 012 { п , q } ср { п , q }