Усечение (геометрия)

Усеченный квадрат представляет собой правильный восьмиугольник: т{4} = {8} 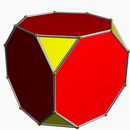=	Усеченный куб t{4,3} или	Усеченные кубические соты т{4,3,4} или

В геометрии усечение — это операция в любом измерении, которая разрезает вершины многогранника , создавая новую фасет вместо каждой вершины. Этот термин происходит от архимедовых названия Кеплером тел .

Равномерное усечение

В общем, любой многогранник (или многогранник) также может быть усечен с определенной степенью свободы относительно глубины разреза, как показано в нотации многогранника Конвея операции усечения .

Особый вид усечения, обычно подразумеваемый, — это равномерное усечение , оператор усечения, применяемый к правильному многограннику (или правильному многограннику ), который создает в результате однородный многогранник ( однородный многогранник ) с равными длинами ребер. Здесь нет степеней свободы, и он представляет собой фиксированную геометрическую форму, как и правильные многогранники.

В общем, все однокольцевые однородные многогранники имеют равномерное усечение. Например, икосододекаэдр , представленный в виде символов Шлефли r{5,3} или ${\begin{Bmatrix}5\\3\end{Bmatrix}}$ и диаграмма Кокстера-Динкина или имеет равномерное усечение, усеченный икосододекаэдр , представленный как tr{5,3} или $t{\begin{Bmatrix}5\\3\end{Bmatrix}}$ , . На диаграмме Кокстера-Динкина эффект усечения заключается в том, чтобы окольцевать все узлы, соседние с окольцованным узлом.

Равномерное усечение, выполненное на регулярной треугольной мозаике {3,6}, приводит к правильной шестиугольной мозаике {6,3}.

Усечение полигонов

Усеченный n-сторонний многоугольник будет иметь 2n сторон (ребер). Правильный многоугольник, равномерно усеченный, станет другим правильным многоугольником: t{n} равно {2n}. Полное усечение (или исправление ) r{3} — это еще один правильный многоугольник в его двойственном положении.

Правильный многоугольник также можно представить с помощью диаграммы Кокстера-Динкина : и его равномерное усечение и его полное усечение . График представляет группу Коксетера I ₂ (n), где каждый узел представляет собой зеркало, а край представляет угол π/ n между зеркалами, а вокруг одного или обоих зеркал дан круг, чтобы показать, какие из них активны.

Параметрические усечения треугольника
{3}		т{3} = {6}		г{3} = {3}

Звездчатые многоугольники также можно обрезать. Усеченная пентаграмма {5/2} будет выглядеть как пятиугольник , но на самом деле представляет собой дважды покрытый (вырожденный) десятиугольник ({10/2}) с двумя наборами перекрывающихся вершин и ребер. Усеченная большая гептаграмма {7/3} дает тетрадекаграмму {14/3}.

Равномерное усечение в правильных многогранниках и мозаиках и выше.

Когда «усечение» применяется к платоновым телам или правильным мозаикам , обычно подразумевается «равномерное усечение», что означает усечение до тех пор, пока исходные грани не станут правильными многоугольниками с вдвое большим количеством сторон, чем исходная форма.

Эта последовательность показывает пример усечения куба с использованием четырех шагов непрерывного процесса усечения между полным кубом и исправленным кубом. Конечный многогранник — кубооктаэдр . Среднее изображение — равномерный усеченный куб ; он представлен символом Шлефли t { p , q ,...}.

Битовое усечение — это более глубокое усечение, при котором удаляются все исходные ребра, но остается внутренняя часть исходных граней. Пример: усеченный октаэдр — это усеченный побитно куб: t{3,4} = 2t{4,3}.

Полное усечение битов, называемое биректификацией , сводит исходные грани к точкам. Для многогранников это становится двойственным многогранником . Пример: октаэдр — это биректификация куба : {3,4} = 2r{4,3}.

Другой тип усечения, кантелляция , обрезает ребра и вершины, удаляет исходные ребра, заменяет их прямоугольниками, удаляет исходные вершины и заменяет их гранями двойственных исходным правильным многогранникам или замощению.

Многогранники более высокой размерности имеют более высокие усечения. Ранцинация режет грани, ребра и вершины. В пяти измерениях стерилизация разрезает клетки, грани и края.

Усечение края

Усечение ребер куба, создание куба со скошенной фаской.

Усечение ребер — это скос или фаска многогранников, аналогичный кантелляции, но с сохранением исходных вершин и заменой ребер шестиугольниками. В 4-многогранниках при усечении ребер ребра заменяются вытянутыми ячейками бипирамиды .

Чередование или частичное усечение

Равномерное чередование усеченного кубооктаэдра дает неоднородный курносый куб .

Чередование или частичное усечение удаляет только некоторые исходные вершины.

При частичном усечении или чередовании половина вершин и соединительных ребер полностью удаляются. Операция применима только к многогранникам с четными гранями. Грани уменьшаются вдвое, а квадратные грани вырождаются в ребра. Например, тетраэдр — это чередующийся куб h{4,3}.

Уменьшение — это более общий термин, используемый в отношении тел Джонсона для удаления одной или нескольких вершин, ребер или граней многогранника, не нарушая при этом другие вершины. Например, трехмерный икосаэдр начинается с правильного икосаэдра с удаленными тремя вершинами.

Другие частичные усечения основаны на симметрии; например, тетраэдрически уменьшенный додекаэдр .

Обобщенные усечения

Процесс линейного усечения можно обобщить, разрешив параметрические усечения, которые являются отрицательными или выходят за пределы средней точки ребер, вызывая самопересекающиеся звездчатые многогранники, и могут параметрически относиться к некоторым правильным звездчатым многоугольникам и однородным звездчатым многогранникам .

Неглубокое усечение — длина ребер уменьшается, грани усекаются, чтобы иметь вдвое больше сторон, при этом новые грани с центром в старых вершинах. формируются
Равномерное усечение является частным случаем этого случая с одинаковой длиной ребер. Усеченный куб t{4,3}, квадратные грани которого становятся восьмиугольниками, а новые треугольные грани являются вершинами.
Антиусечение Обратное неглубокое усечение , усекающее исходные края наружу, а не внутрь. В результате получается многогранник, который выглядит как оригинал, но части двойника свисают с его углов, а не разрезаются на собственные углы.
Полное усечение или исправление . Предел неглубокого усечения, при котором края сводятся к точкам. r {4,3}. кубооктаэдр Примером может служить
Гиперусечение. Форма усечения, проходящая после исправления, инвертирующая исходные края и вызывающая появление самопересечений.
Квазиусечение. Форма усечения, заходящая даже дальше, чем гиперусечение, при которой инвертированное ребро становится длиннее исходного. Его можно сгенерировать из исходного многогранника, рассматривая все грани как ретроградные, то есть идущие назад вокруг вершины. Например, квазиусечение квадрата дает правильную октаграмму (t{4,3}={8/3}), а квазиусечение куба дает однородный звездчатый усеченный шестигранник t{4/3,3}.

Усечения на квадрате
Типы усечения квадрата {4}: исходные края показаны красным, а новые усеченные края — голубым. Равномерный усеченный квадрат — это правильный восьмиугольник, t{4}={8}. Полный усеченный квадрат становится новым квадратом с диагональной ориентацией. Вершины располагаются по порядку против часовой стрелки, 1–4, с усеченными парами вершин как a и b .

Усечение куба
⇨ t _aC	Куб {4,3} С	⇨ tC	Усечение t{4,3} tC	⇨ tC	Полное усечение г{4,3} до н.э.	⇩ t _hC
Антиусечение t _a C						Гиперусечение t _h C
⇧ t _aC	Полное квазиусечение а _q C	⇦	Квазиусечение t{4/3,3} t _q C	⇦ t _qC	Полное гиперусечение a _h C	⇦ t _hC

См. также

Ссылки

Коксетер, Правильные многогранники HSM (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 (стр. 145–154, глава 8: Усечение)
Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.

Внешние ссылки

Вайсштейн, Эрик В. «Усечение» . Математический мир .
Ольшевский, Георгий. «Усечение» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
Имена многогранников, усечение

Операторы многогранника
v
т
и
Семя	Усечение	Исправление	Биусечение	Двойной	Расширение	Всеобрезание	Чередования


$т 0 {п, q} {п, q}$	$т 01 {п, q} т {п, q}$	$т 1 {п, q} р {п, q}$	$т 12 {п, q} 2t{п, q}$	$т 2 {п, q} 2r{п, q}$	$т 02 {п, q} рр {п, q}$	$т 012 {п, q} тр {п, q}$	$чт 0 {п, q} ч {q, п}$	$чт 12 {п, q} с {q, п}$	$чт 012 {п, q} ср {п, q}$