Кантелляция (геометрия)

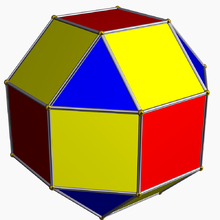
Зубчатые . кубические соты - Фиолетовые кубики имеют зубчатую форму Края скошены, образуя новые синие кубические ячейки. Вершины усекаются, образуя новые красные выпрямленные ячейки куба .

В геометрии кантелляция в любом 2-го порядка — это усечение измерении, которое скашивает по правильный многогранник его краям , и вершинам создавая новую грань вместо каждого ребра и каждой вершины. Кантелляция также применима к обычным плиткам и сотам . Кантелляция многогранника — это также спрямление его спрямления .

Кантелляция (для многогранников и мозаик) также называется расширением Алисии Буль Стотт : она соответствует перемещению граней правильной формы от центра и заполнению новой грани в зазоре для каждого открытого ребра и для каждой открытой вершины.

Обозначения

Согнутый многогранник представляется расширенным символом Шлефли t _0,2 { p , q ,...} или r ${\begin{Bmatrix}p\\q\\...\end{Bmatrix}}$ или rr { p , q ,...}.

Для многогранников кантелляция предлагает прямую последовательность от правильного многогранника к его двойственному .

Пример: последовательность сопряжений между кубом и октаэдром:

Пример: кубооктаэдр — это согнутый тетраэдр .

Для многогранников более высокой размерности кантелляция предлагает прямую последовательность от правильного многогранника к его биректифицированной форме.

Примеры: сочленяющиеся многогранники, мозаики.

Правильные многогранники, правильные мозаики
Форма	Многогранники			плитки
Коксетер	РТТ	rCO	избавлять	rQQ	rHΔ
Конвей обозначение	И	ЭК = еО	еI = еD	эквалайзер	еН = еΔ
Многогранники быть расширен	Тетраэдр	Куб или октаэдр	Икосаэдр или додекаэдр	Квадратная плитка	Шестиугольная плитка Треугольная плитка
Многогранники быть расширен
Изображение
Анимация

Однородные многогранники или их двойники.
Коксетер	ррт{2,3}	ррс{2,6}	rrCO	ррИД
Конвей обозначение	EP3	еА4	еаО = еаС	eaI = eaD
Многогранники быть расширен	Треугольная призма или треугольная бипирамида	Квадратная антипризма или тетрагональный трапецоэдр	Кубооктаэдр или ромбический додекаэдр	Икосидодекаэдр или ромбический триаконтаэдр
Многогранники быть расширен
Изображение
Анимация

См. также

Ссылки

Коксетер, Правильные многогранники HSM (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 (стр. 145–154, глава 8: Усечение, стр. 210, расширение)
Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.

Внешние ссылки

Вайсштейн, Эрик В. «Расширение» . Математический мир .

Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее .