Курносый многогранник

Многогранник
Сорт	Количество и свойства
Платоновые тела	( 5 , выпуклый, правильный)
Архимедовы тела	( 13 , выпуклый, однородный)
Многогранники Кеплера – Пуансо	( 4 , правильный, невыпуклый)
Однородные многогранники	( 75 , униформа)
Призматоид : призмы , антипризмы и т. д.	( 4 бесконечных однородных класса)
Замощения многогранников	( 11 обычных , в самолете)
Квазиправильные многогранники	( 8 )
Твердые вещества Джонсона	( 92 , выпуклая, неоднородная)
Бипирамиды	( бесконечный )
Пирамиды	( бесконечный )
Звездочки	Звездочки
Полиэдрические соединения	( 5 обычных )
Дельтаэдры	( Дельтаэдры , грани равностороннего треугольника)
Курносые многогранники	( 12 униформ , не зеркальное отображение)
Зоноэдр	( Зоноэдры , грани имеют симметрию 180°)
Двойной многогранник
Самодвойственный многогранник	( бесконечный )
Каталонский солид	( 13 , архимедово двойственное)

В геометрии — курносый многогранник это многогранник, полученный выполнением операции курносого : чередования соответствующего всеусеченного или усеченного многогранника, в зависимости от определения. Некоторые, но не все, авторы относят антипризмы к курносым многогранникам, поскольку они получаются в результате этой конструкции из вырожденного «многогранника» только с двумя гранями ( диэдра ).

Киральные курносые многогранники не всегда обладают зеркальной симметрией и поэтому иногда имеют две энантиоморфные (лево- и правостороннюю) формы, которые являются отражением друг друга. Их группы симметрии — все точечные группы .

Например, курносый куб :

Курносые многогранники имеют символ Витхоффа | pqr и, как следствие, конфигурация вершин 3. p .3. д .3. р . Многогранники с ретро-взносом (подмножество курносого многогранника, содержащее большой икосаэдр , малый икосикосододекаэдр с ретро-взносом и большой икосододекаэдр с ретро-взносом ) по-прежнему имеют эту форму символа Витхоффа, но вместо этого их конфигурации вершин ⁠ ${\frac {(3.-p.3.-q.3.-r)}{2}}.$⁠

Список курносых многогранников

Униформа

Существует 12 однородных курносых многогранников, не считая антипризм, икосаэдра как курносого тетраэдра , большого икосаэдра как ретровзносого тетраэдра и большого несплюснутого диромбидодекаэдра , также известного как фигура Скиллинга .

Когда треугольник Шварца курносого многогранника равнобедренный , курносый многогранник не является киральным. Это относится к антипризмам, икосаэдру , большому икосаэдру , малому курносому икосикосододекаэдру и малому ретровзносому икосикосододекаэдру .

На изображениях курносого вывода (показывающих искаженный курносый многогранник, топологически идентичный однородной версии, полученный в результате геометрического чередования родительского однородного всеусеченного многогранника), где зеленый цвет отсутствует, грани, полученные в результате чередования, окрашены в красный и желтый цвета, а курносые треугольники синие. Там, где присутствует зеленый цвет (только для курносого икосододекадодекаэдра и большого курносого додецикозододекаэдра ), грани, полученные в результате чередования, имеют красный, желтый и синий цвет, а курносые треугольники - зеленый.

Курносый многогранник	Изображение	Исходный всеусеченный многогранник	Изображение	Курносое происхождение	Группа симметрии	Символ Витхоффа Описание вершины
Икосаэдр ( курносый тетраэдр )		Усеченный октаэдр			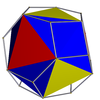Я ч ( Т ч	| 3 3 2 3.3.3.3.3
Большой икосаэдр ( взносносый тетраэдр )		Усеченный октаэдр			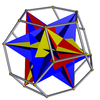Я ч ( Т ч	| 2 3 / 2 3 / 2 (3.3.3.3.3) / 2
Курносый куб или курносый кубооктаэдр		Усеченный кубооктаэдр			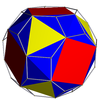ТО	| 4 3 2 3.3.3.3.4
Курносый додекаэдр или курносый икосододекаэдр		Усеченный икосододекаэдр			я	| 5 3 2 3.3.3.3.5
Маленький курносый икосикосидодекаэдр		Двукратно покрытый усеченный икосаэдр			I h	| 3 3 5 / 2 3.3.3.3.3. 5 / 2
Курносый додекадодекаэдр		Маленький ромбидодекаэдр с дополнительным 12{ 10 / 2 } лица			я	| 5 5 / 2 2 3.3. 5 / 2 .3.5
Курносый икосододекадодекаэдр		Икосусеченный додекадодекаэдр			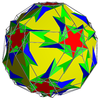я	| 5 3 5 / 3 3. 5 / 3 .3.3.3.5
Большой курносый икосододекаэдр		Ромбикосаэдр с дополнительным 12{ 10 / 2 } лица			я	| 3 5 / 2 2 3.3. 5 / 2 .3.3
Перевернутый курносый додекадодекаэдр		Усеченный додекадодекаэдр			я	| 5 2 5 / 3 3. 5 / 3 .3.3.3.5
Большой курносый додецикосододекаэдр		Большой додетикосаэдр с дополнительным 12{ 10 / 2 } лица		изображения пока нет	я	| 3 5 / 2 5 / 3 3. 5 / 3 .3. 5 / 2 .3.3
Большой перевернутый курносый икосододекаэдр.		Большой усеченный икосододекаэдр			я	| 3 2 5 / 3 3. 5 / 3 .3.3.3
Малый ретровзносый икосикосододекаэдр		Двукратно покрытый усеченный икосаэдр		изображения пока нет	I h	| 5 / 2 3 / 2 3 / 2 (3.3.3.3.3. 5 / 2 ) / 2
Большой ретроносый икосододекаэдр		Большой ромбидодекаэдр с дополнительными 20{ 6 / 2 } лица		изображения пока нет	я	| 2 5 / 3 3 / 2 (3.3.3. 5 / 2 .3) / 2
Большой диромбикосидодекаэдр		—	—	—	I h	| 3 / 2 5 / 3 3 5 / 2 (4. 3 / 2 .4. 5 / 3 .4.3.4. 5 / 2 ) / 2
Большой диснуб диромбидодекаэдр		—	—	—	I h	| ( 3 / 2 ) 5 / 3 (3) 5 / 2 ( 3 / 2 . 3 / 2 . 3 / 2 .4. 5 / 3 .4.3.3.3.4. 5 / 2 .4) / 2

Примечания:

• Икосаэдр и , курносый куб курносый додекаэдр — единственные три выпуклые . Они получены взносом усеченного октаэдра , усеченного кубооктаэдра и усеченного икосододекаэдра — трех выпуклых усеченных квазиправильных многогранников .
• Единственный курносый многогранник с киральной октаэдрической группой симметрий — это курносый куб .
• Только икосаэдр и большой икосаэдр также являются правильными многогранниками . Они также являются дельтаэдрами .
• Только икосаэдр, большой икосаэдр, малый курносый икосикосододекаэдр , малый ретроносый икосикосододекаэдр , большой диромбикосододекаэдр и большой курносый диромбидодекаэдр также обладают отражательной симметрией.

Существует также бесконечное множество антипризм . Они образуются из призм , представляющих собой усеченные осоэдры , вырожденные правильные многогранники . Те, что до шестиугольной формы, перечислены ниже. На рисунках, показывающих курносое отведение, грани, полученные в результате чередования (оснований призм), окрашены в красный цвет, а курносые треугольники - в желтый цвет. Исключением является тетраэдр, у которого все грани представляют собой красные курносые треугольники, поскольку чередование квадратных оснований куба приводит к вырождению двуугольников в качестве граней.

Курносый многогранник	Изображение	Исходный всеусеченный многогранник	Изображение	Курносое происхождение	Группа симметрии	Символ Витхоффа Описание вершины
Тетраэдр		Куб		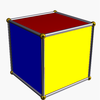	Т д ( Д 2д )	| 2 2 2 3.3.3
Октаэдр		Шестиугольная призма		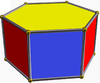	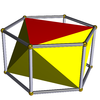Ох ​ ( D 3d )	| 3 2 2 3.3.3.3
Квадратная антипризма		Восьмиугольная призма			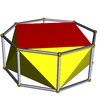Д 4д	| 4 2 2 3.4.3.3
Пятиугольная антипризма		Десятиугольная призма			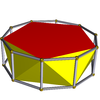Д 5д	| 5 2 2 3.5.3.3
Пентаграмматическая антипризма		с двойным покрытием Пятиугольная призма			Д 5ч	| 5 / 2 2 2 3. 5 / 2 .3.3
Пентаграмматическая скрещенная антипризма		Декаграммная призма			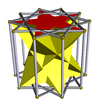Д 5д	| 2 2 5 / 3 3. 5 / 3 .3.3
Шестиугольная антипризма		Додекагональная призма		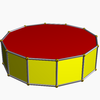	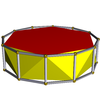Д 6д	| 6 2 2 3.6.3.3

Примечания:

• Два из этих многогранников могут быть построены из первых двух курносых многогранников в списке, начиная с икосаэдра : пятиугольная антипризма представляет собой парабидоуменьшенный икосаэдр , а пентаграммная скрещенная антипризма представляет собой парабидиуменьшенный большой икосаэдр, также известный как парабидополненный большой икосаэдр .

Неравномерный

Два тела Джонсона представляют собой курносые многогранники: курносый дисфеноид и курносая квадратная антипризма . Ни один из них не является хиральным.

Курносый многогранник	Изображение	Оригинальный многогранник	Изображение	Группа симметрии
Курносый дисфеноид		дисфеноид		Д 2д
Курносая квадратная антипризма		Квадратная антипризма		Д 4д

Ссылки

• Коксетер, Гарольд Скотт Макдональд ; Лонге-Хиггинс, MS; Миллер, JCP (1954), «Равномерные многогранники», Философские труды Лондонского королевского общества. Series A. Mathematical and Physical Sciences , 246 (916): 401–450, doi : 10.1098/rsta.1954.0003 , ISSN   0080-4614 , JSTOR   91532 , MR   0062446 , S2CID   202575183
• Веннингер, Магнус (1974). Модели многогранников . Издательство Кембриджского университета. ISBN  0-521-09859-9 .
• Скиллинг, Дж. (1975), «Полный набор однородных многогранников», Философские труды Лондонского королевского общества. Series A. Mathematical and Physical Sciences , 278 (1278): 111–135, doi : 10.1098/rsta.1975.0022 , ISSN   0080-4614 , JSTOR   74475 , MR   0365333 , S2CID   122634260
• Мэдер Р.Э. Равномерные многогранники. Математика Дж. 3, 48–57, 1993.

Операторы многогранника

Семя	Усечение	Исправление	Биусечение	Двойной	Расширение	Всеобрезание	Чередования
т 0 { п , q } { п , q }	т 01 { п , q } т { п , q }	т 1 { п , q } р { п , q }	т 12 { п , q } 2t{ п , q }	т 2 { п , q } 2r{ п , q }	т 02 { п , q } рр { п , q }	т 012 { п , q } тр { п , q }	чт 0 { п , q } ч { q , п }	чт 12 { п , q } с { q , п }	чт 012 { п , q } ср { п , q }