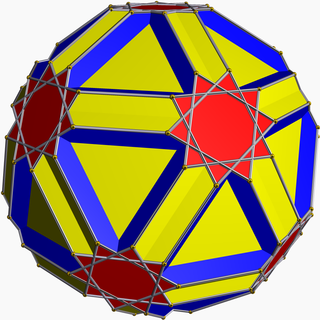
Икосусеченный додекадодекаэдр

Икосусеченный додекадодекаэдр
Тип	Однородный звездчатый многогранник
Элементы	Ф = 44, Е = 180 V = 120 (χ = −16)
Лица по сторонам	20{6}+12{10}+12{10/3}
Диаграмма Кокстера
Символ Витхоффа	3 5 5/3 |
Группа симметрии	I h , [5,3], *532
Ссылки на индексы	Ю 45 , С 57 , Ж 84
Двойной многогранник	Тридьякис икосаэдр
Вершинная фигура	6.10.10/3
Аббревиатура Бауэрса	Идди

3D-модель икосусеченного додекадодекаэдра

В геометрии или икосусеченный додекадодекаэдр икосидодекадодекаэдр представляет собой невыпуклый однородный многогранник , обозначаемый как U ₄₅ .

Выпуклая оболочка

Его выпуклая оболочка представляет собой неоднородный усеченный икосододекаэдр .

Усеченный икосододекаэдр

Выпуклая оболочка

Икосусеченный додекадодекаэдр

Декартовы координаты

Декартовы координаты вершин икосусеченного додекадодекаэдра — это все четные перестановки $${\begin{array}{crrlc}{\Bigl (}&\pm {\bigl [}2-{\frac {1}{\varphi }}{\bigr ]},&\pm \,1,&\pm {\bigl [}2+\varphi {\bigr ]}&{\Bigr )},\\{\Bigl (}&\pm \,1,&\pm \,{\frac {1}{\varphi ^{2}}},&\pm {\bigl [}3\varphi -1{\bigr ]}&{\Bigr )},\\{\Bigl (}&\pm \,2,&\pm \,{\frac {2}{\varphi }},&\pm \,2\varphi &{\Bigr )},\\{\Bigl (}&\pm \,3,&\pm \,{\frac {1}{\varphi ^{2}}},&\pm \,\varphi ^{2}&{\Bigr )},\\{\Bigl (}&\pm \,\varphi ^{2},&\pm \,1,&\pm {\bigl [}3\varphi -2{\bigr ]}&{\Bigr )},\end{array}}$$

где $\varphi ={\tfrac {1+{\sqrt {5}}}{2}}$ это золотое сечение .

Связанные многогранники

Тридьякис икосаэдр

Тридьякис икосаэдр
Тип	Звездный многогранник
Лицо
Элементы	Ф = 120, Е = 180 V = 44 (χ = −16)
Группа симметрии	I h , [5,3], *532
Ссылки на индексы	ДУ 45
двойной многогранник	Икосусеченный додекадодекаэдр

— Икосаэдр тридиакис это двойственный многогранник икосусеченного додекадодекаэдра. Он имеет 44 вершины, 180 ребер и 120 разносторонних треугольных граней.

См. также

• Каталонские сплошные двойники к выпуклым однородным многогранникам
• Однородные многогранники
• Список однородных многогранников

Ссылки

• Веннингер, Магнус (1983), Двойные модели , Издательство Кембриджского университета , ISBN  978-0-521-54325-5 , MR   0730208 Фотография на стр. 96, построение Дормана Люка и звездчатый узор на стр. 97.

Внешние ссылки

• Вайсштейн, Эрик В. «Икосусеченный додекадодекаэдр» . Математический мир .