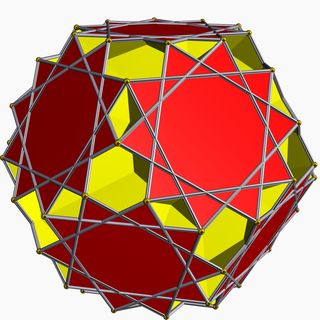
Большой додекикосаэдр

Большой додекикосаэдр
Тип	Однородный звездчатый многогранник
Элементы	Ф = 32, Е = 120 V = 60 (χ = −28)
Лица по сторонам	20{6}+12{10/3}
Диаграмма Кокстера	(с дополнительными треугольниками с двойным покрытием) (с дополнительными пятиугольниками с двойным покрытием)
Символ Витхоффа	3 5/3 (3/2 5/2) |
Группа симметрии	I h , [5,3], *532
Ссылки на индексы	Ю 63 , С 79 , Ж 101
Двойной многогранник	Большой додецикосакрон
Вершинная фигура	6.10/3.6/5.10/7
Аббревиатура Бауэрса	Головокружительный

3D-модель большого додетикосаэдра

В геометрии большой додекикосаэдр (или большой додекикосаэдр ) представляет собой невыпуклый однородный многогранник , имеющий индекс _U63 . У него 32 грани (20 шестиугольников и 12 декаграмм ), 120 ребер и 60 вершин. Его вершинная фигура представляет собой перекрещенный четырехугольник .

Он имеет составной символ Витхоффа , 3 5 ⁄ 3 ( 3 ⁄ 2 5 ⁄ 2 ) |, требуются два разных треугольника Шварца : (3 для создания которого 5 ⁄ 3 3 ⁄ 2 ) и (3 5 ⁄ 3 5 ⁄ 2 ). ( 3 5 ⁄ 3 3 ⁄ 2 | представляет собой большой додетикосаэдр с дополнительным 12 { 10 ⁄ 2 } пятиугольника и 3 5 ⁄ 3 5 ⁄ 2 | представляет его с дополнительными 20 { 6 ⁄ 2 } треугольников.)

Его вершина рисунок 6. 10 ⁄ 3 . 6 ⁄ 5 . 10 ⁄ 7 также неоднозначно: вокруг каждой вершины имеется две грани по часовой стрелке и две грани против часовой стрелки.

Связанные многогранники

Он разделяет расположение вершин с усеченным додекаэдром . Кроме того, он имеет такое же расположение ребер, что и большой икосикосододекаэдр (имеющий общие шестиугольные грани) и большой дитригональный додецикосододекаэдр (имеющий общие декаграммные грани).

Усеченный додекаэдр

Большой икосикосододекаэдр

Большой дитригональный додецикосододекаэдр

Большой додекикосаэдр

Галерея

Традиционная начинка

Заполнение по модулю-2

См. также

• Список однородных многогранников

Внешние ссылки

• Вайсштейн, Эрик В. «Большой додетикосаэдр» . Математический мир .