Курносые 24-ячеистые соты

Курносые 24-ячеистые соты
(Нет изображения)
Тип	Униформа 4-сотовая
Символы Шлефли	с{3,4,3,3} ср{3,3,4,3} 2ср{4,3,3,4} 2ср{4,3,3 ^1,1} с{3 ^1,1,1,1}
Диаграммы Кокстера	=
4-гранный тип	курносый 24-клеточный 16-ячеечный 5-клеточный
Тип ячейки	{3,3} {3,5}
Тип лица	треугольник {3}
Вершинная фигура	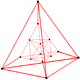Неправильный декахорон
Симметрии	[3 ⁺,4,3,3] [3,4,(3,3) ⁺] [4,(3,3) ⁺,4] [4,(3,3 ^1,1) ⁺] [3 ^1,1,1,1] ⁺
Характеристики	Вершина транзитивная , невитоффова

В четырехмерной евклидовой геометрии курносые соты из 24 ячеек или курносые икоситетрахорические соты представляют собой однородную мозаику (или соты ), заполняющую пространство, состоящую из курносых 24 ячеек , 16 ячеек и 5 ячеек . Он был открыт Торольдом Госсетом в его статье 1900 года о полуправильных многогранниках. Он не полуправильный по определению правильных граней Госсетом, но все его ячейки ( гребни ) правильные, либо тетраэдры , либо икосаэдры .

Его можно рассматривать как чередование усеченных сот из 24 ячеек и представить символом Шлефли s{3,4,3,3}, s{3 ^1,1,1,1} и 3 другие курносые конструкции.

Он определяется неправильной фигурой вершины декахорона (10-клеточный 4-клеточный многогранник), ограненной четырьмя курносыми 24-ячеечными , одной 16-ячеечной и пятью 5-ячеечными . Фигуру вершины топологически можно рассматривать как модифицированную тетраэдрическую призму , где один из тетраэдров разделен на средних гранях на центральный октаэдр и четыре угловых тетраэдра. Тогда четыре боковые грани призмы, треугольные призмы, превращаются в трехмерные икосаэдры .

Симметричные конструкции

Существует пять различных конструкций симметрии этой мозаики. Каждая симметрия может быть представлена различным расположением цветных курносых 24- , 16- и 5-ячеечных граней. Во всех случаях в каждой вершине встречаются четыре курносых 24-клетки, пять 5-клеток и одна 16-клетка , но вершинные фигуры имеют разные генераторы симметрии.

Симметрия	Коксетер Шлефли	Фасеты (на фигуре вершины )
Симметрия	Коксетер Шлефли	Курносый 24-клеточный (4)	16-ячеечный (1)	5-клеточный (5)
[3 ⁺,4,3,3]	с{3,4,3,3}	4:
[3,4,(3,3) ⁺]	ср{3,3,4,3}	3: 1:
[[4,(3,3) ⁺,4]]	2ср{4,3,3,4}	2,2:
[(3 ^1,1,3) ⁺,4]	2ср{4,3,3 ^1,1}	1,1: 2:
[3 ^1,1,1,1] ⁺	с{3 ^1,1,1,1}	1,1,1,1:

См. также

Правильные и однородные соты в 4-мерном пространстве:

Ссылки

Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики , Макмиллан, 1900 г.
Коксетер, Правильные многогранники HSM (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 стр. 296, Таблица II: Обычные соты
Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
Георгий Ольшевский, Равномерные паноплоидные тетракомбы , Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб) Модель 133
Клитцинг, Ричард. «4D евклидовы мозаики» . , о4с3с3с4о, с3с3с *б3с4о, с3с3с *б3с *б3с, о3о3о4с3с, с3с3с4о3о - садит - О133

v т и Основные выпуклые правильные и однородные соты размеров 2–9.
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
И ²	Равномерная укладка плитки	{3 ^[3]}	д ₃	HD ₃	квартал ₃	Шестиугольный
И ³	Равномерные выпуклые соты	{3 ^[4]}	д ₄	HD ₄	4 _{квартала}
И ⁴	Униформа 4-сотовая	{3 ^[5]}	д ₅	hδ ₅	qδ ₅	24-ячеистые соты
И ⁵	Униформа 5-сотовая	{3 ^[6]}	д ₆	HD ₆	qδ ₆
И ⁶	Униформа 6-сотовая	{3 ^[7]}	д ₇	hδ ₇	qδ ₇	2 ₂₂
И ⁷	Униформа 7-сотовая	{3 ^[8]}	д ₈	hδ ₈	8 _{кварталов}	1 ₃₃ • 3 ₃₁
И ⁸	Униформа 8-сотовая	{3 ^[9]}	д ₉	HD ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
И ⁹	Униформа 9-сотовая	{3 ^[10]}	д ₁₀	HD ₁₀	10 _{кварталов}
И ¹⁰	Униформа 10-сотовая	{3 ^[11]}	д ₁₁	HD ₁₁	qδ ₁₁
И ^{п -1}	Равномерный ( n -1)- сотовый	{3 ^[н]}	δ _н	hδ _н	qδ _н	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁