Альтернативные гиперкубические соты

Чередование квадратной плитки или шахматной доски . или	Расширенная квадратная плитка.
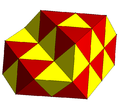Частично заполненные чередующиеся кубические соты с тетраэдрическими и октаэдрическими ячейками. 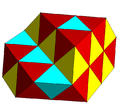или	Субсимметричные цветные чередующиеся кубические соты.

В геометрии ( чередующиеся соты гиперкуба или демикубические соты ) — это размерная бесконечная серия сот , основанная на сотах гиперкуба с операцией чередования . Дан символ Шлефли h{4,3...3,4}, представляющий правильную форму с удаленной половиной вершин и содержащий симметрию группы Коксетера. ${\tilde {B}}_{n-1}$ для n ≥ 4. Форма нижней симметрии ${\tilde {D}}_{n-1}$ четвертого порядка можно создать, удалив еще одно зеркало на пике .

Перемежающиеся фасеты гиперкуба становятся полугиперкубами , а удаленные вершины создают новые ортоплекса фасеты . Вершинной фигурой сот этого семейства являются выпрямленные ортоплексы.

Их также называют hδ _n, что означает (n-1)-мерные соты.

hδ н	Имя	Шлефли символ	Семья симметрии
			${\tilde {B}}_{n-1}$ [4,3 n-4 ,3 1,1 ]	${\tilde {D}}_{n-1}$ [3 1,1 ,3 n-5 ,3 1,1 ]
			Диаграммы Кокстера-Динкина по семействам
hδ 2	Апейрогон	{∞}
HD 3	Чередование квадратной плитки (То же, что и {4,4})	ч{4,4}=т 1 {4,4} т 0,2 {4,4}
HD 4	Переменные кубические соты	ч{4,3,4} {3 1,1 ,4}
hδ 5	16-ячеечный тетракомб (То же, что и {3,3,4,3})	ч{4,3 2 ,4} {3 1,1 ,3,4} {3 1,1,1,1 }
HD 6	5-кубовые соты	ч{4,3 3 ,4} {3 1,1 ,3 2 ,4} {3 1,1 ,3,3 1,1 }
hδ 7	6-кубовые соты	ч{4,3 4 ,4} {3 1,1 ,3 3 ,4} {3 1,1 ,3 2 ,3 1,1 }
hδ 8	7-кубовые соты	ч{4,3 5 ,4} {3 1,1 ,3 4 ,4} {3 1,1 ,3 3 ,3 1,1 }
HD 9	8-кубовые соты	ч{4,3 6 ,4} {3 1,1 ,3 5 ,4} {3 1,1 ,3 4 ,3 1,1 }
hδ н	n-демикубические соты	ч{4,3 n-3 ,4} {3 1,1 ,3 n-4 ,4} {3 1,1 ,3 n-5 ,3 1,1 }	...

Ссылки

• Коксетер, Правильные многогранники HSM (3-е издание, 1973 г.), Дуврское издание, ISBN   0-486-61480-8
  1. С. 122–123, 1973. (Решетка гиперкубов γ _n образует кубические соты , δ _n+1 )
  2. стр. 154–156: Частичное усечение или чередование, представленное префиксом h : h{4,4}={4,4}; ч{4,3,4}={3 ^1,1 ,4}, ч{4,3,3,4}={3,3,4,3}
  3. п. 296, Таблица II: Правильные соты, δ _n+1
• Калейдоскопы: избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
  • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]

скрывать Основные выпуклые правильные и однородные соты размеров 2–9.
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
И 2	Равномерная укладка плитки	{3 [3] }	д 3	HD 3	квартал 3	Шестиугольный
И 3	Равномерные выпуклые соты	{3 [4] }	д 4	HD 4	4 квартала
И 4	Униформа 4-сотовая	{3 [5] }	д 5	hδ 5	qδ 5	24-ячеистые соты
И 5	Униформа 5-сотовая	{3 [6] }	д 6	HD 6	qδ 6
И 6	Униформа 6-сотовая	{3 [7] }	д 7	hδ 7	qδ 7	2 22
И 7	Униформа 7-сотовая	{3 [8] }	д 8	hδ 8	8 кварталов	1 33 • 3 31
И 8	Униформа 8-сотовая	{3 [9] }	д 9	HD 9	qδ 9	1 52 • 2 51 • 5 21
И 9	Униформа 9-сотовая	{3 [10] }	д 10	HD 10	10 кварталов
И 10	Униформа 10-сотовая	{3 [11] }	д 11	HD 11	qδ 11
И п -1	Равномерный ( n -1)- сотовый	{3 [н] }	δ н	hδ н	qδ н	1 лиц 2 • 2 лиц 1 • лиц 21