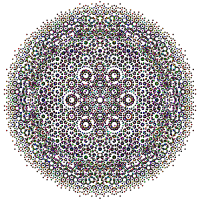
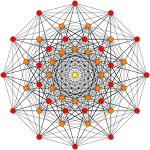
4 21 многогранник

4 21	1 42	2 41
Исправлено 4 21	Исправлено 1 42	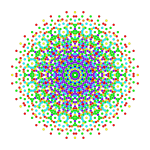Исправлено 2 41
Биректифицированный 4 21	Триректифицированный 4 21
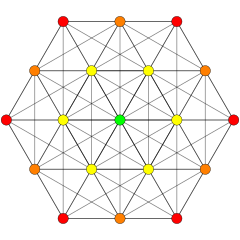
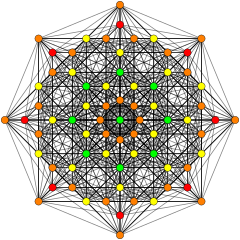
Ортогональные проекции в E 6 плоскости Кокстера

В 8-мерной 21 представляет геометрии 4 _собой полуправильный однородный 8-многогранник , построенный в рамках симметрии E ₈ группы . Он был открыт Торольдом Госсетом и опубликован в его статье 1900 года. Он назвал ее 8-й полуправильной фигурой .

Его символ Кокстера — 4 ₂₁ , описывающий его разветвляющуюся диаграмму Кокстера-Динкина с одним кольцом на конце 4-узловой последовательности, .

Выпрямленный 4 ₂₁ строится по точкам на средних краях 4 ₂₁ . Биректифицированное число 4 ₂₁ строится из точек в центрах граней треугольника 4 ₂₁ . Триректифицированное число 4 ₂₁ построено точками в центрах тетраэдра 4 ₂₁ .

Эти многогранники являются частью семейства 255 = 2. ⁸ − 1 выпуклый однородный 8-многогранник , состоящий из однородных 7-многогранников и вершинных фигур , определяемый всеми перестановками одного или нескольких колец в этой диаграмме Кокстера-Динкина: .

4 ₂₁ многогранник

4 21
Тип	Равномерный 8-многогранник
Семья	к 21 многогранник
Символ Шлефли	{3,3,3,3,3 2,1 }
Символ Коксетера	4 21
Диаграммы Кокстера	=
7-гранный	19440 всего: 2160 4 11 17280 {3 6 }
6-гранный	207360: 138240 {3 5 } 69120 {3 5 }
5-гранный	483840 {3 4 }
4-ликий	483840 {3 3 }
Клетки	241920 {3,3}
Лица	60480 {3}
Края	6720
Вершины	240
Вершинная фигура	3 21 многогранник
Полигон Петри	30-угольник
Группа Коксетера	Е 8 , [3 4,2,1 ], заказ 696729600
Характеристики	выпуклый

Многогранник 4 ₂₁ имеет 17 280 7-симплексных и 2160 7-ортоплексных граней и 240 вершин. Его вершинная фигура — многогранник 3 ₂₁ . Поскольку его вершины представляют собой векторы простой группы Ли E8 _{корневые} , этот многогранник иногда называют E8 _{многогранником} корневым .

Вершины этого многогранника также можно получить, взяв 240 целых октонионов нормы 1. Поскольку октонионы представляют собой неассоциативную нормированную алгебру с делением , эти 240 точек подвергаются операции умножения, превращающей их не в группу, а в петлю , фактически в петлю. Петля Муфанг .

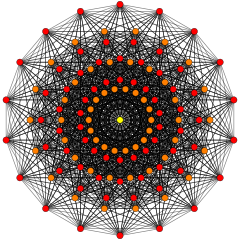
Для визуализации этот 8-мерный многогранник часто отображается в специальном наклоненном ортогональном направлении проекции, которое помещает его 240 вершин в правильный триаконтагон (называемый многоугольником Петри ). Его 6720 ребер нарисованы между 240 вершинами. На этой проекции также можно выделить и нарисовать конкретные высшие элементы (грани, ячейки и т.п.).

Альтернативные названия

• Этот многогранник был открыт Торольдом Госсетом , который описал его в своей статье 1900 года как 8-мерную полуправильную фигуру . Это последняя конечная полуправильная фигура в его перечислении, полуправильная для него означает, что она содержит только правильные грани.
• Э. Л. Эльте назвал его V ₂₄₀ (из-за 240 вершин) в своем списке полуправильных многогранников 1912 года.
• HSM Coxeter назвал его 4 ₂₁ , потому что его диаграмма Кокстера-Динкина имеет три ветви длиной 4, 2 и 1 с единственным узлом на конечном узле 4-й ветви.
• Dischiliahectoexpata-myriaheptachiliadiacosioctaconta-zetton (аббревиатура Fy) - 2160-17280 граненый полизеттон (Джонатан Бауэрс)

Он создан с помощью конструкции Витгофа на основе набора из 8 гиперплоских зеркал в 8-мерном пространстве.

240 вершин многогранника 4 ₂₁ можно составить в два набора: 112 ( 2 ² × ⁸ C ₂ ) с координатами, полученными из $(\pm 2,\pm 2,0,0,0,0,0,0)\,$ взяв произвольную комбинацию знаков и произвольную перестановку координат, и 128 корней (2 ⁷ ) с координатами, полученными из $(\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1)\,$ взяв четное количество знаков минус (или, что то же самое, потребовав, чтобы сумма всех восьми координат была кратна 4).

Каждая вершина имеет 56 ближайших соседей; например, ближайшие соседи вершины $(1,1,1,1,1,1,1,1)$ - это те, чьи координаты в сумме равны 4, а именно 28, полученные перестановкой координат $(2,2,0,0,0,0,0,0)\,$ и 28, полученные перестановкой координат $(1,1,1,1,1,1,-1,-1)$. Эти 56 точек являются вершинами многогранника 3 ₂₁ в 7 измерениях.

Каждая вершина имеет 126 вторых ближайших соседей: например, ближайшие соседи вершины $(1,1,1,1,1,1,1,1)$ - это те, чьи координаты в сумме равны 0, а именно 56, полученные перестановкой координат $(2,-2,0,0,0,0,0,0)\,$ и 70, полученные перестановкой координат $(1,1,1,1,-1,-1,-1,-1)$. Эти 126 точек являются вершинами многогранника 2 ₃₁ в 7 измерениях.

Каждая вершина также имеет 56 третьих ближайших соседей, которые являются отрицательными по отношению к ее ближайшим соседям, и одну антиподальную вершину, всего $1+56+126+56+1=240$ вершины.

Другая конструкция заключается в использовании знаковой комбинации из 14 кодовых слов 8-битного расширенного кода Хэмминга (8,4), что дает 14 × 2 ⁴ = 224 вершины и добавление тривиальной оси со знаком $(\pm 2,0,0,0,0,0,0,0)$ для последних 16 вершин. В этом случае вершины представляют собой расстояние ${\sqrt {4}}$ от происхождения, а не ${\sqrt {8}}$.

 Hamming 8-bit Code
 0  0 0 0 0 0 0 0 0
 1  1 1 1 1 0 0 0 0   ⇒   ± ± ± ± 0 0 0 0
 2  1 1 0 0 1 1 0 0   ⇒   ± ± 0 0 ± ± 0 0
 3  0 0 1 1 1 1 0 0   ⇒   0 0 ± ± ± ± 0 0
 4  1 0 1 0 1 0 1 0   ⇒   ± 0 ± 0 ± 0 ± 0        ±2 0 0 0 0 0 0 0
 5  0 1 0 1 1 0 1 0   ⇒   0 ± 0 ± ± 0 ± 0        0 ±2 0 0 0 0 0 0
 6  0 1 1 0 0 1 1 0   ⇒   0 ± ± 0 0 ± ± 0        0 0 ±2 0 0 0 0 0
 7  1 0 0 1 0 1 1 0   ⇒   ± 0 0 ± 0 ± ± 0        0 0 0 ±2 0 0 0 0
 8  0 1 1 0 1 0 0 1   ⇒   0 ± ± 0 ± 0 0 ±        0 0 0 0 ±2 0 0 0
 9  1 0 0 1 1 0 0 1   ⇒   ± 0 0 ± ± 0 0 ±        0 0 0 0 0 ±2 0 0
 A  1 0 1 0 0 1 0 1   ⇒   ± 0 ± 0 0 ± 0 ±        0 0 0 0 0 0 ±2 0
 B  0 1 0 1 0 1 0 1   ⇒   0 ± 0 ± 0 ± 0 ±        0 0 0 0 0 0 0 ±2
 C  1 1 0 0 0 0 1 1   ⇒   ± ± 0 0 0 0 ± ±
 D  0 0 1 1 0 0 1 1   ⇒   0 0 ± ± 0 0 ± ±
 E  0 0 0 0 1 1 1 1   ⇒   0 0 0 0 ± ± ± ±
 F  1 1 1 1 1 1 1 1
                          ( 224 vertices     +     16 vertices )

Другое разложение дает 240 точек в 9 измерениях в виде расширенного 8-симплекса . и два противоположных биректифицированных 8-симплекса , и .

⁠ $(3,-3,0,0,0,0,0,0,0)$⁠ : 72 вершины

⁠ $(-2,-2,-2,1,1,1,1,1,1)$⁠ : 84 вершины

⁠ $(2,2,2,-1,-1,-1,-1,-1,-1)$⁠ : 84 вершины

Это возникает аналогично связи решетки A8 и решетки E8 , имеющих 8 зеркал A8: .

A7 Проекции плоскости Кокстера

Имя	4 21	расширенный 8-симплекс	биректифицированный 8-симплекс	биректифицированный 8-симплекс
Вершины	240	72	84	84
Изображение

Мозаика

Этот многогранник является вершинной фигурой равномерной мозаики 8-мерного пространства, представленной символом 5 ₂₁ и диаграммой Кокстера-Динкина:

Конструкция и лица

Информацию о фасетах этого многогранника можно извлечь из его диаграммы Кокстера-Динкина :

Удаление узла на короткой ветви оставляет 7-симплекс :

Удаление узла на конце ветви длиной 2 оставляет 7-ортоплекс в его чередующейся форме ( 4 ₁₁ ):

Каждая 7-симплексная фасета касается только 7-ортоплексных фасетов, в то время как альтернативные фасеты ортоплексной фасета касаются либо симплекса, либо другого ортоплекса. Всего имеется 17 280 симплексных фасетов и 2160 ортоплексных фасетов.

Поскольку каждый 7-симплекс имеет 7 6-симплексных граней, каждая из которых не инцидентна ни одному другому 6-симплексу, многогранник 4 ₂₁ имеет 120 960 (7 × 17 280) 6-симплексных граней, которые являются гранями 7-симплексов. Поскольку каждый 7-ортоплекс имеет 128 (2 ⁷ ) 6-симплексных граней, половина из которых не инцидентны 7-симплексам, многогранник 4 ₂₁ имеет 138 240 (2 ⁶ ×2160) 6-симплексные грани, не являющиеся гранями 7-симплексов. Таким образом, многогранник 4 ₂₁ имеет два типа 6-симплексных граней, не взаимозаменяемых симметриями этого многогранника. Общее количество 6-симплексных граней равно 259200 (120960+138240).

Фигура вершины однокольцевого многогранника получается путем удаления окольцованного узла и окольцовывания его соседей. Это делает многогранник 3 ₂₁ .

В матрице конфигурации количество элементов может быть получено путем удаления зеркал и соотношений групповых порядков Кокстера .

show		Матрица конфигурации
E8		k-face	fk	f0	f1	f2	f3	f4	f5	f6		f7		k-figure	notes
E7		( )	f0	240	56	756	4032	10080	12096	4032	2016	576	126	3_21 polytope	E8/E7 = 192×10!/(72×8!) = 240
A1E6		{ }	f1	2	6720	27	216	720	1080	432	216	72	27	2_21 polytope	E8/A1E6 = 192×10!/(2×72×6!) = 6720
A2D5		{3}	f2	3	3	60480	16	80	160	80	40	16	10	5-demicube	E8/A2D5 = 192×10!/(6×24×5!) = 60480
A3A4		{3,3}	f3	4	6	4	241920	10	30	20	10	5	5	Rectified 5-cell	E8/A3A4 = 192×10!/(4!×5!) = 241920
A4A2A1		{3,3,3}	f4	5	10	10	5	483840	6	6	3	2	3	Triangular prism	E8/A4A2A1 = 192×10!/(5!×3!×2) = 483840
A5A1		{3,3,3,3}	f5	6	15	20	15	6	483840	2	1	1	2	Isosceles triangle	E8/A5A1 = 192×10!/(6!×2) = 483840
A6		{3,3,3,3,3}	f6	7	21	35	35	21	7	138240	*	1	1	{ }	E8/A6 = 192×(10!×7!) = 138240
A6A1				7	21	35	35	21	7	*	69120	0	2		E8/A6A1 = 192×10!/(7!×2) = 69120
A7		{3,3,3,3,3,3}	f7	8	28	56	70	56	28	8	0	17280	*	( )	E8/A7 = 192×10!/8! = 17280
D7		{3,3,3,3,3,4}		14	84	280	560	672	448	64	64	*	2160		E8/D7 = 192×10!/(26×7!) = 2160

Прогнозы

График 4 21, созданный в виде стринг-арта .

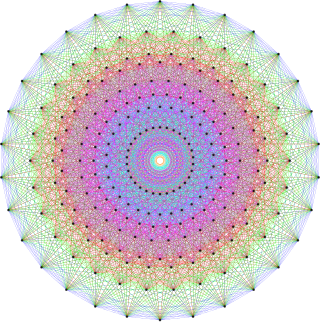E 8 Проекция плоскости Кокстера

3D

Математическое представление физической модели Зоме, изоморфной (?) E8. Он построен на основе VisibLie_E8 , изображенного со всеми 3360 ребрами длины √ 2 ( √ 5 −1) из двух концентрических ячеек по 600 (в золотом сечении) с ортогональными проекциями на перспективное трехмерное пространство.

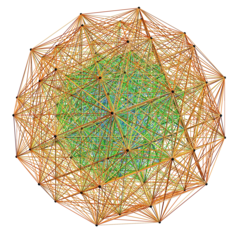Фактический разделенный реальный четный многогранник E8 4 21 , спроецированный в перспективное трехмерное пространство, изображенный со всеми 6720 ребрами длины √ 2

E8 повернута в H4+H4φ, спроецирована в 3D, преобразована в STL и напечатана на нейлоновом пластике. Использованная основа прогноза: х = {1, φ, 0, −1, φ, 0,0,0} y = {φ, 0, 1, φ, 0, −1,0,0} z = {0, 1, φ, 0, −1, φ,0,0}

2D

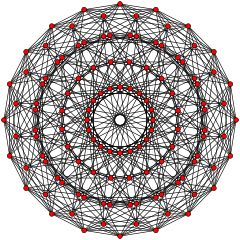
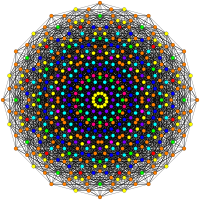
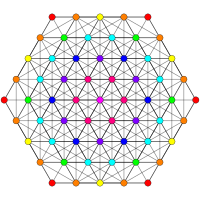
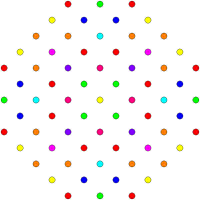
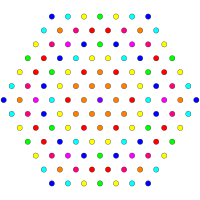
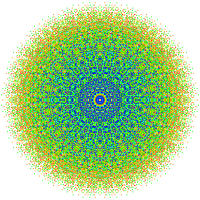
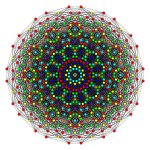
Эти графики представляют собой ортогональные проекции в _E8 , _E7 , _E6 и _B8 , _D8 , _D7 , _D6 , _D5 , _D4 D3 _, A7 _, , _A5 плоскостях Кокстера . Цвета вершин определяются перекрывающейся кратностью в проекции: они окрашиваются в порядке возрастания кратности: красный, оранжевый, желтый, зеленый.

showОртогональные проекции
E8 / H4 [30]	[20]	[24]
(Colors: 1)	(Colors: 1)	(Colors: 1)
E7 [18]	E6 / F4 [12]	[6]
(Colors: 1,3,6)	(Colors: 1,8,24)	(Colors: 1,2,3)
D3 / B2 / A3 [4]	D4 / B3 / A2 / G2 [6]	D5 / B4 [8]
(Colors: 1,12,32,60)	(Colors: 1,27,72)	(Colors: 1,8,24)
D6 / B5 / A4 [10]	D7 / B6 [12]	D8 / B7 / A6 [14]
(Colors: 1,5,10,20)	(Colors: 1,3,9,12)	(Colors: 1,2,3)
B8 [16/2]	A5 [6]	A7 [8]
(Colors: 1)	(Colors: 3,8,24,30)	(Colors: 1,2,4,8)

к ₂₁ семья

Многогранник 4 ₂₁ является последним в семействе, называемом k ₂₁ многогранниками . Первый многогранник в этом семействе — полуправильная треугольная призма , составленная из трёх квадратов (2-ортоплексов) и двух треугольников (2-симплексов).

Геометрическое складывание

Многогранник 4 ₂₁ можно спроецировать в трехмерное пространство как физическую модель ребер вершин. Здесь изображены две концентрические ячейки по 600 (в золотом сечении) с использованием инструментов Zome . (Не все из 3360 ребер длины √ 2 ( √ 5 -1) представлены.)

Число 4 ₂₁ связано с числом 600 ячеек геометрическим сворачиванием диаграмм Кокстера-Дынкина . Это можно увидеть на проекциях плоскости Кокстера E8/H4 . 240 вершин многогранника 4 ₂₁ проецируются в 4-мерное пространство как две копии 120 вершин 600-ячеечного многогранника, одна копия меньше (масштабируется золотым сечением ), чем другая с той же ориентацией. Если рассматривать 2D ортогональную проекцию на плоскость Коксетера E8/H4, 120 вершин 600-ячеистой ячейки проецируются в тех же четырех кольцах, что и в 4 ₂₁ . Остальные 4 кольца графа 4 ₂₁ также соответствуют уменьшенной копии четырех колец 600-ячейки.

showE8/H4 Складки плоскости Кокстера
E8	H4
421	600-cell
[20] symmetry planes
421	600-cell

Связанные многогранники

В 4-мерной комплексной геометрии правильный комплексный многогранник ₃ {3} ₃ {3} ₃ {3} ₃ и диаграмма Кокстера существует с тем же расположением вершин, что и многогранник 4 ₂₁ . Оно самодвойственно. Коксетер назвал его многогранником Уиттинга в честь Александра Уиттинга . Коксетер выражает симметрию группы Шепарда как ₃ [3] ₃ [3] ₃ [3] ₃ .

4 ₂₁ является шестым в размерной серии полуправильных многогранников . Каждый прогрессивный однородный многогранник является вершинной фигурой предыдущего многогранника. Торольд Госсет определил эту серию в 1900 году как содержащую все правильные многогранные грани, содержащие все симплексы и ортоплексы .

показывать k 21 фигура в n измерениях
Space	Finite						Euclidean	Hyperbolic
En	3	4	5	6	7	8	9	10
Coxeter group	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9 = ${\tilde {E}}_{8}$ = E8+	E10 = ${\bar {T}}_{8}$ = E8++
Coxeter diagram
Symmetry	[3−1,2,1]	[30,2,1]	[31,2,1]	[32,2,1]	[33,2,1]	[34,2,1]	[35,2,1]	[36,2,1]
Order	12	120	1,920	51,840	2,903,040	696,729,600	∞
Graph							-	-
Name	−121	021	121	221	321	421	521	621

Выпрямленный многогранник 4_21

Исправлено 4 21
Тип	Равномерный 8-многогранник
Символ Шлефли	т 1 {3,3,3,3,3 2,1 }
Символ Коксетера	т 1 (4 21 )
Диаграмма Кокстера
7-гранный	19680 всего: 240 3 21 17280 т 1 {3 6 } 2160 т 1 {3 5 ,4}
6-гранный	375840
5-гранный	1935360
4-ликий	3386880
Клетки	2661120
Лица	1028160
Края	181440
Вершины	6720
Вершинная фигура	2 21 призма
Группа Коксетера	Е 8 , [3 4,2,1 ]
Характеристики	выпуклый

Выпрямленный 4 ₂₁ можно рассматривать как выпрямление многогранника 4 ₂₁ , создающее новые вершины в центре ребер 4 ₂₁ .

Альтернативные названия

• Ректифицированный дисхилиахектогексаконта-мириагептачилиадиакозиоктаконта-зеттон для ректифицированного полизеттона 2160-17280 (аббревиатура Риффи) (Джонатан Бауэрс)

Строительство

Он создан с помощью конструкции Витгофа на основе набора из 8 гиперплоских зеркал в 8-мерном пространстве. Он назван в честь ректификации числа 4 ₂₁ . Вершины располагаются в середине всех ребер 4 ₂₁ и новых ребер, соединяющих их.

Информацию о фасетах можно извлечь из диаграммы Кокстера-Динкина .

Удаление узла на короткой ветви оставляет исправленный 7-симплекс :

Удаление узла на конце ветви длиной 2 оставляет выпрямленный 7-ортоплекс в его чередующейся форме:

Удаление узла на конце ветки длиной 4 оставляет 3 ₂₁ :

Фигура вершины определяется удалением окольцованного узла и добавлением кольца к соседнему узлу. Получается призма 2 ₂₁ .

Координаты

Декартовы координаты 6720 вершин выпрямленного 4 ₂₁ задаются всеми перестановками координат из трех других однородных многогранников:

• шестигранный 8-куб - нечетные отрицания: ½(±1,±1,±1,±1,±1,±1,±3,±3) - 3584 вершины
• биректифицированный 8-куб - (0,0,±1,±1,±1,±1,±1,±1) - 1792 вершины
• зубчатый 8-ортоплекс - (0,0,0,0,0,0,±1,±1,±2) - 1344 вершины

D8 Проекции плоскости Кокстера

Имя	Исправлено 4 21	биректифицированный 8-куб =	шестигранный 8-кубический =	кантеллированный 8-ортоплекс =
Вершины	6720	1792	3584	1344
Изображение

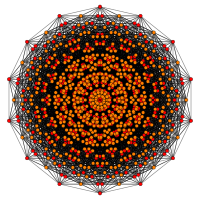
Прогнозы

2D

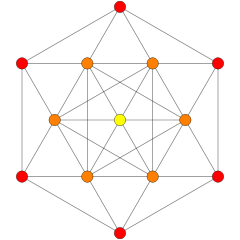
Эти графики представляют собой ортогональные проекции в _E8 , _E7 , _E6 и _B8 , _D8 , _D7 , _D6 , _D5 , _D4 D3 _, A7 _, , _A5 плоскостях Кокстера . Цвета вершин определяются перекрывающейся кратностью в проекции: они окрашиваются в порядке возрастания кратности: красный, оранжевый, желтый, зеленый.

showОртогональные проекции
E8 / H4 [30]	[20]	[24]
E7 [18]	E6 / F4 [12]	[6]
D3 / B2 / A3 [4]	D4 / B3 / A2 / G2 [6]	D5 / B4 [8]
D6 / B5 / A4 [10]	D7 / B6 [12]	D8 / B7 / A6 [14]
B8 [16/2]	A5 [6]	A7 [8]

Биректифицированный многогранник 4_21

Биректифицированный 4 21 многогранник
Тип	Равномерный 8-многогранник
Символ Шлефли	т 2 {3,3,3,3,3 2,1 }
Символ Коксетера	т 2 (4 21 )
Диаграмма Кокстера
7-гранный	19680 всего: 17280 т 2 {3 6 } 2160 т 2 {3 5 ,4} 240 т 1 (3 21 )
6-гранный	382560
5-гранный	2600640
4-ликий	7741440
Клетки	9918720
Лица	5806080
Края	1451520
Вершины	60480
Вершинная фигура	5-полукубическая — треугольная дуопризма
Группа Коксетера	Е 8 , [3 4,2,1 ]
Характеристики	выпуклый

Двуисправленный 4 ₂₁ можно рассматривать как второе выпрямление однородного многогранника 4 ₂₁ . Вершины этого многогранника расположены в центрах всех 60480 треугольных граней 4 ₂₁ .

Альтернативные названия

• Биректифицированный дисхилиахектогексаконта-мириагептачилиадиакозиоктаконта-зеттон для биректифицированного 2160-17280 полизеттона (аббревиатура borfy) (Джонатан Бауэрс)

Строительство

Он создан с помощью конструкции Витгофа на основе набора из 8 гиперплоских зеркал в 8-мерном пространстве. Он назван в честь биректификации числа 4 ₂₁ . Вершины расположены в центре всех граней треугольника 4 ₂₁ .

Информацию о фасетах можно извлечь из диаграммы Кокстера-Динкина .

Удаление узла на короткой ветви оставляет биректифицированный 7-симплекс . Таких граней 17280.

Удаление узла на конце ветви длиной 2 оставляет биректифицированный 7-ортоплекс в его чередующейся форме. Таких граней 2160.

Удаление узла на конце ветви длиной 4 оставляет выпрямленный 3 ₂₁ . Таких граней 240.

Фигура вершины определяется удалением окольцованного узла и добавлением колец к соседним узлам. Получается 5-полукубическая дуопризма треугольной формы.

Прогнозы

2D

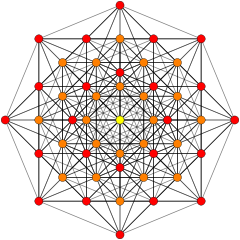
Эти графики представляют собой ортогональные проекции в _E8 , _E7 , _E6 и _B8 , _D8 , _D7 , _D6 , _D5 , _D4 D3 _, A7 _, , _A5 плоскостях Кокстера . Края не прорисованы. Цвета вершин определяются перекрывающейся кратностью в проекции: они окрашиваются в порядке возрастания кратности: красный, оранжевый, желтый, зеленый и т. д.

showОртогональные проекции
E8 / H4 [30]	[20]	[24]
E7 [18]	E6 / F4 [12]	[6]
D3 / B2 / A3 [4]	D4 / B3 / A2 / G2 [6]	D5 / B4 [8]
D6 / B5 / A4 [10]	D7 / B6 [12]	D8 / B7 / A6 [14]
B8 [16/2]	A5 [6]	A7 [8]

Триректифицированный многогранник 4_21

4 21 Триректифицированный многогранник
Тип	Равномерный 8-многогранник
Символ Шлефли	т 3 {3,3,3,3,3 2,1 }
Символ Коксетера	т 3 (4 21 )
Диаграмма Кокстера
7-гранный	19680
6-гранный	382560
5-гранный	2661120
4-ликий	9313920
Клетки	16934400
Лица	14515200
Края	4838400
Вершины	241920
Вершинная фигура	тетраэдр - выпрямленная 5-ячеечная дуопризма
Группа Коксетера	Е 8 , [3 4,2,1 ]
Характеристики	выпуклый

Альтернативные названия

• Триректифицированный дисхилиагектогексаконта-мириагептахилиадиакозиоктаконта-зеттон для триректифицированного 2160-17280 полизеттона (аббревиатура торфи) (Джонатан Бауэрс)

Строительство

Он создан с помощью конструкции Витгофа на основе набора из 8 гиперплоских зеркал в 8-мерном пространстве. Он назван в честь биректификации числа 4 ₂₁ . Вершины расположены в центре всех граней треугольника 4 ₂₁ .

Информацию о фасетах можно извлечь из диаграммы Кокстера-Динкина .

Удаление узла на короткой ветви оставляет триисправленный 7-симплекс :

Удаление узла на конце ветви длиной 2 оставляет триректифицированный 7-ортоплекс в его чередующейся форме:

Удаление узла на конце ветки длиной 4 оставляет биректифицированный 3 ₂₁ :

Фигура вершины определяется путем удаления окольцованного узла и окольцовывания соседних узлов. Получается тетраэдр – выпрямленная 5-ячеечная дуопризма.

Прогнозы

2D

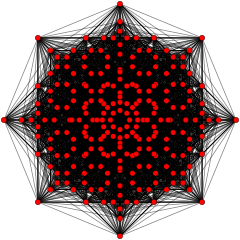
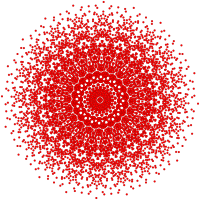
Эти графики представляют собой ортогональные проекции в _E7 , _E6 , _B8 , _D8 , _D7 , _D6 , _D5 , _D4 , _D3 , _A7 и _A5 плоскостях Кокстера . Цвета вершин определяются перекрывающейся кратностью в проекции: они окрашиваются в порядке возрастания кратности: красный, оранжевый, желтый, зеленый.

(E ₈ и B ₈ были слишком большими для отображения)

showОртогональные проекции
E7 [18]	E6 / F4 [12]	D4 - E6 [6]
D3 / B2 / A3 [4]	D4 / B3 / A2 / G2 [6]	D5 / B4 [8]
D6 / B5 / A4 [10]	D7 / B6 [12]	D8 / B7 / A6 [14]
A5 [6]	A7 [8]

См. также

• Список многогранников E8

Ссылки

• Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900 г.
• Эльте, EL (1912), Полуправильные многогранники гиперпространств , Гронинген: Гронингенский университет.
• Коксетер, HSM , Правильные комплексные многогранники , Издательство Кембриджского университета, (1974).
• Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена , Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
  • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45] См. стр. 347 (рисунок 3.8c) Питера Макмаллена : (30-угольный граф узлов и ребер из 4 ₂₁ )
• Клитцинг, Ричард. «8D однородные многогранники (polyzetta)» . o3o3o3o *c3o3o3o3x - фй, o3o3o3o *c3o3o3x3o - риффи, o3o3o3o *c3o3x3o3o - борфи, o3o3o3o *c3x3o3o3o - торфий