1 22 многогранник
 1 22 |  Исправлено 1 22 | 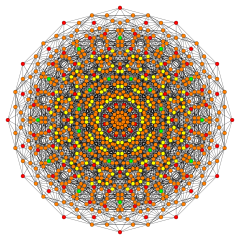 Биректифицированный 1 22 |
 2 21 | 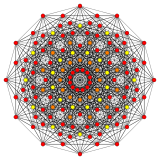 Исправлено 2 21 | |
| ортогональные проекции в E 6 плоскости Кокстера | ||
|---|---|---|
В 6-мерной геометрии многогранник 1 22 — это однородный многогранник , построенный из группы E 6 . Впервые он был опубликован в списке полуправильных многогранников Э. Л. Эльте в 1912 году, названном V 72 (из-за 72 вершин). [1]
Его символ Кокстера — 1 22 , описывающий его разветвляющуюся диаграмму Кокстера-Динкина с одним кольцом на конце последовательности из 1 узла. Имеются два ректификации числа 1 22 , построенные по положениям точек на элементах числа 1 22 . Выпрямленный 1 22 строится по точкам на средних краях 1 22 . Биректифицированное 1 22 строится точками в центрах треугольных граней 1 22 .
Эти многогранники входят в семейство из 39 выпуклых однородных многогранников в 6-мерном измерении , состоящих из однородных фасет многогранников и фигур вершин , определяемых всеми перестановками колец в этой диаграмме Кокстера-Дынкина : ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
1 22 многогранник
[ редактировать ]| 1 22 многогранник | |
|---|---|
| Тип | Равномерный 6-многогранник |
| Семья | 1 k2 многогранник |
| Символ Шлефли | {3,3 2,2 } |
| Символ Коксетера | 1 22 |
| Диаграмма Кокстера-Динкина | |
| 5-гранный | 54: 27 1 21 27 1 21 |
| 4-ликий | 702: 270 1 11 432 1 20 |
| Клетки | 2160: 1080 1 10 1080 {3,3} |
| Лица | 2160 {3} |
| Края | 720 |
| Вершины | 72 |
| Вершинная фигура | Биректифицированный 5-симплекс : 0 22  |
| Полигон Петри | Додекагон |
| Группа Коксетера | Е 6 , [[3,3 2,2 ]], заказ 103680 |
| Характеристики | выпуклый , изотопный |
Многогранник 1 22 содержит 72 вершины и 54 5-демикубических грани. Он имеет биректифицированную 5-симплексную вершинную фигуру . Его 72 вершины представляют собой корневые векторы простой группы Ли E 6 .
Альтернативные названия
[ редактировать ]- Пентаконтатетра-петон (Акроним Мо) — 54-гранный полипетон (Джонатан Бауэрс) [2]
Изображения
[ редактировать ]| Е6 [12] | Д5 [8] | Д4/А2 [6] | |
|---|---|---|---|
 (1,2) | 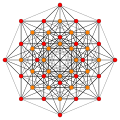 (1,3) |  (1,9,12) | |
| Б6 [12/2] | А5 [6] | A4 [[5]] = [10] | А3/Д3 [4] |
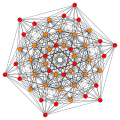 (1,2) | 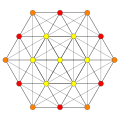 (2,3,6) | 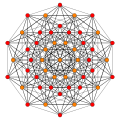 (1,2) | 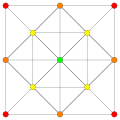 (1,6,8,12) |
Строительство
[ редактировать ]Он создан с помощью конструкции Витхоффа на основе набора из 6 гиперплоских зеркал в 6-мерном пространстве.
Информацию о фасетах можно извлечь из диаграммы Кокстера-Динкина . ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Удаление узла на любой из ветвей длиной 2 оставляет 5-полукуб , 1 31 , ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Фигура вершины определяется путем удаления окольцованного узла и окольцовывания соседнего узла. Это делает биректифицированный 5-симплекс , 0 22 , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
В матрице конфигурации количество элементов может быть получено путем удаления зеркал и соотношений групповых порядков Кокстера . [3]
| EЕ6 | k-лицо | ж к | ж 0 | ж 1 | ff2 | f 3 | ж 4 | ж 5 | к -фигура | примечания | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AА5 | ( ) | ж 0 | 72 | 20 | 90 | 60 | 60 | 15 | 15 | 30 | 6 | 6 | г {3,3,3} | Е 6 /А 5 = 72*6!/6! = 72 | |
| А 2 А 2 А 1 | { } | ж 1 | 2 | 720 | 9 | 9 | 9 | 3 | 3 | 9 | 3 | 3 | {3}×{3} | Е 6 /А 2 А 2 А 1 = 72*6!/3!/3!/2 = 720 | |
| А 2 А 1 А 1 | {3} | ff2 | 3 | 3 | 2160 | 2 | 2 | 1 | 1 | 4 | 2 | 2 | с{2,4} | Е 6 /А 2 А 1 А 1 = 72*6!/3!/2/2 = 2160 | |
| А 3 А 1 | {3,3} | f 3 | 4 | 6 | 4 | 1080 | * | 1 | 0 | 2 | 2 | 1 | { }∨( ) | Е 6 /А 3 А 1 = 72*6!/4!/2 = 1080 | |
| 4 | 6 | 4 | * | 1080 | 0 | 1 | 2 | 1 | 2 | ||||||
| А 4 А 1 | {3,3,3} | ж 4 | 5 | 10 | 10 | 5 | 0 | 216 | * | * | 2 | 0 | { } | Е 6 /А 4 А 1 = 72*6!/5!/2 = 216 | |
| 5 | 10 | 10 | 0 | 5 | * | 216 | * | 0 | 2 | ||||||
| Д 4 | ч{4,3,3} | 8 | 24 | 32 | 8 | 8 | * | * | 270 | 1 | 1 | Е 6 /Д 4 = 72*6!/8/4! = 270 | |||
| Д 5 | ч{4,3,3,3} | ж 5 | 16 | 80 | 160 | 80 | 40 | 16 | 0 | 10 | 27 | * | ( ) | Е 6 /Д 5 = 72*6!/16/5! = 27 | |
| 16 | 80 | 160 | 40 | 80 | 0 | 16 | 10 | * | 27 | ||||||
Связанный сложный многогранник
[ редактировать ]
Правильный комплексный многогранник 3 {3} 3 {4} 2 , ![]()
![]()
![]()
![]()
![]() , в имеет вещественное представление в виде многогранника 1 22 в 4-мерном пространстве. Он имеет 72 вершины, 216 3-рёбер и 54 3{3}3 грани. Его комплексная группа отражений равна 3 [3] 3 [4] 2 порядка 1296. Она имеет полусимметрию квазирегулярной конструкции как
, в имеет вещественное представление в виде многогранника 1 22 в 4-мерном пространстве. Он имеет 72 вершины, 216 3-рёбер и 54 3{3}3 грани. Его комплексная группа отражений равна 3 [3] 3 [4] 2 порядка 1296. Она имеет полусимметрию квазирегулярной конструкции как ![]()
![]()
![]()
![]()
![]() , как выпрямление гессенского многогранника ,
, как выпрямление гессенского многогранника , ![]()
![]()
![]()
![]()
![]() . [4]
. [4]
Связанные многогранники и соты
[ редактировать ]Наряду с полуправильным многогранником 2 21 он также является одним из семейства из 39 выпуклых однородных многогранников в 6-мерных измерениях, состоящих из однородных граней многогранника и вершинных фигур , определяемых всеми перестановками колец в этой диаграмме Кокстера-Дынкина : ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
| 1 k2 фигур в n измерениях |
|---|
Геометрическое складывание
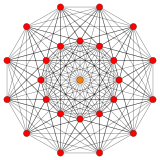
[ редактировать ]Число 122 6 измерениях, F4 — связано с 24-ячейкой геометрической складкой E6 → F4 диаграмм Кокстера-Динкина , E6 соответствует 122 в с 24 ячейками в 4 измерениях. Это можно увидеть в проекциях плоскости Кокстера . 24 вершины 24-клетки проецируются в те же два кольца, что и в 1 22 .
| Самолеты E6/F4 Коксетера | |
|---|---|
 1 22 |  24-ячеечный |
| Самолеты D4/B4 Коксетера | |
 1 22 |  24-ячеечный |
Мозаика
[ редактировать ]Этот многогранник является вершинной фигурой для равномерной мозаики 6-мерного пространства, 2 22 , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
1 22 Выпрямленный многогранник
[ редактировать ]| Исправлено 1 22 | |
|---|---|
| Тип | Равномерный 6-многогранник |
| Символ Шлефли | 2р{3,3,3 2,1 } г{3,3 2,2 } |
| Символ Коксетера | 0 221 |
| Диаграмма Кокстера-Динкина | или |
| 5-гранный | 126 |
| 4-ликий | 1566 |
| Клетки | 6480 |
| Лица | 6480 |
| Края | 6480 |
| Вершины | 720 |
| Вершинная фигура | Призма 3-3 дуопризмы |
| Полигон Петри | Додекагон |
| Группа Коксетера | Е 6 , [[3,3 2,2 ]], заказ 103680 |
| Характеристики | выпуклый |
Выпрямленный многогранник 1 22 (также называемый 0 221 ) может замощить 6-мерное пространство как ячейку Вороного сотовой решетки E6 * (двойственной решетке E6). [5]
Альтернативные названия
[ редактировать ]- Биректифицированный 2 21 многогранник
- Rectified pentacontatetrapeton (аббревиатура Ram ) — выпрямленный 54-гранный полипетон (Джонатан Бауэрс) [6]
Изображения
[ редактировать ]Вершины окрашены в соответствии с их кратностью в этой проекции в прогрессивном порядке: красный, оранжевый, желтый.
| Е6 [12] | Д5 [8] | Д4/А2 [6] | Б6 [12/2] |
|---|---|---|---|
 |  | 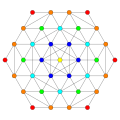 | 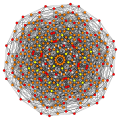 |
| А5 [6] | A4 [5] | А3/Д3 [4] | |
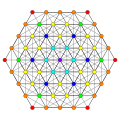 |  | 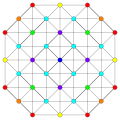 |
Строительство
[ редактировать ]Его конструкция основана на группе E 6 , а информацию можно извлечь из кольцевой диаграммы Кокстера-Динкина, представляющей этот многогранник: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Удаление кольца на короткой ветви оставляет биректифицированный 5-симплекс , ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Удаление кольца на любой из ветвей длины 2 оставляет биректифицированный 5-ортоплекс в его чередующейся форме: t 2 (2 11 ) , ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Фигура вершины определяется удалением окольцованного узла и окольцовыванием соседнего кольца. Получается 3-3 призмы дуопризмы , {3}×{3}×{}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
В матрице конфигурации количество элементов может быть получено путем удаления зеркал и соотношений групповых порядков Кокстера . [7] [8]
| EЕ6 | k-лицо | ж к | ж 0 | ж 1 | ff2 | f 3 | ж 4 | ж 5 | к -фигура | примечания | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| А 2 А 2 А 1 | ( ) | ж 0 | 720 | 18 | 18 | 18 | 9 | 6 | 18 | 9 | 6 | 9 | 6 | 3 | 6 | 9 | 3 | 2 | 3 | 3 | {3}×{3}×{ } | Е 6 /А 2 А 2 А 1 = 72*6!/3!/3!/2 = 720 | |
| А 1 А 1 А 1 | { } | ж 1 | 2 | 6480 | 2 | 2 | 1 | 1 | 4 | 2 | 1 | 2 | 2 | 1 | 2 | 4 | 1 | 1 | 2 | 2 | { }∨{ }∨( ) | Е 6 /А 1 А 1 А 1 = 72*6!/2/2/2 = 6480 | |
| А 2 А 1 | {3} | ff2 | 3 | 3 | 4320 | * | * | 1 | 2 | 1 | 0 | 0 | 2 | 1 | 1 | 2 | 0 | 1 | 2 | 1 | клиновидная | Е 6 /А 2 А 1 = 72*6!/3!/2 = 4320 | |
| 3 | 3 | * | 4320 | * | 0 | 2 | 0 | 1 | 1 | 1 | 0 | 2 | 2 | 1 | 1 | 1 | 2 | ||||||
| А 2 А 1 А 1 | 3 | 3 | * | * | 2160 | 0 | 0 | 2 | 0 | 2 | 0 | 1 | 0 | 4 | 1 | 0 | 2 | 2 | { }∨{ } | Е 6 /А 2 А 1 А 1 = 72*6!/3!/2/2 = 2160 | |||
| А 2 А 1 | {3,3} | f 3 | 4 | 6 | 4 | 0 | 0 | 1080 | * | * | * | * | 2 | 1 | 0 | 0 | 0 | 1 | 2 | 0 | { }∨( ) | Е 6 /А 2 А 1 = 72*6!/3!/2 = 1080 | |
| AА3 | г{3,3} | 6 | 12 | 4 | 4 | 0 | * | 2160 | * | * | * | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | {3} | Е 6 /А 3 = 72*6!/4! = 2160 | ||
| А 3 А 1 | 6 | 12 | 4 | 0 | 4 | * | * | 1080 | * | * | 0 | 1 | 0 | 2 | 0 | 0 | 2 | 1 | { }∨( ) | Е 6 /А 3 А 1 = 72*6!/4!/2 = 1080 | |||
| {3,3} | 4 | 6 | 0 | 4 | 0 | * | * | * | 1080 | * | 0 | 0 | 2 | 0 | 1 | 1 | 0 | 2 | |||||
| г{3,3} | 6 | 12 | 0 | 4 | 4 | * | * | * | * | 1080 | 0 | 0 | 0 | 2 | 1 | 0 | 1 | 2 | |||||
| A 4 | г {3,3,3} | ж 4 | 10 | 30 | 20 | 10 | 0 | 5 | 5 | 0 | 0 | 0 | 432 | * | * | * | * | 1 | 1 | 0 | { } | Е 6 /А 4 = 72*6!/5! = 432 | |
| А 4 А 1 | 10 | 30 | 20 | 0 | 10 | 5 | 0 | 5 | 0 | 0 | * | 216 | * | * | * | 0 | 2 | 0 | Е 6 /А 4 А 1 = 72*6!/5!/2 = 216 | ||||
| A 4 | 10 | 30 | 10 | 20 | 0 | 0 | 5 | 0 | 5 | 0 | * | * | 432 | * | * | 1 | 0 | 1 | Е 6 /А 4 = 72*6!/5! = 432 | ||||
| Д 4 | {3,4,3} | 24 | 96 | 32 | 32 | 32 | 0 | 8 | 8 | 0 | 8 | * | * | * | 270 | * | 0 | 1 | 1 | Е 6 /Д 4 = 72*6!/8/4! = 270 | |||
| А 4 А 1 | г {3,3,3} | 10 | 30 | 0 | 20 | 10 | 0 | 0 | 0 | 5 | 5 | * | * | * | * | 216 | 0 | 0 | 2 | Е 6 /А 4 А 1 = 72*6!/5!/2 = 216 | |||
| AА5 | 2р{3,3,3,3} | ж 5 | 20 | 90 | 60 | 60 | 0 | 15 | 30 | 0 | 15 | 0 | 6 | 0 | 6 | 0 | 0 | 72 | * | * | ( ) | Е 6 /А 5 = 72*6!/6! = 72 | |
| Д 5 | 2р{4,3,3,3} | 80 | 480 | 320 | 160 | 160 | 80 | 80 | 80 | 0 | 40 | 16 | 16 | 0 | 10 | 0 | * | 27 | * | Е 6 /Д 5 = 72*6!/16/5! = 27 | |||
| 80 | 480 | 160 | 320 | 160 | 0 | 80 | 40 | 80 | 80 | 0 | 0 | 16 | 10 | 16 | * | * | 27 | ||||||
Усеченный 1 22 многогранник
[ редактировать ]| Усечено 1 22 | |
|---|---|
| Тип | Равномерный 6-многогранник |
| Символ Шлефли | т{3,3 2,2 } |
| Символ Коксетера | т(1 22 ) |
| Диаграмма Кокстера-Динкина | или |
| 5-гранный | 72+27+27 |
| 4-ликий | 32+216+432+270+216 |
| Клетки | 1080+2160+1080+1080+1080 |
| Лица | 4320+4320+2160 |
| Края | 6480+720 |
| Вершины | 1440 |
| Вершинная фигура | ( )v{3}x{3} |
| Полигон Петри | Додекагон |
| Группа Коксетера | Е 6 , [[3,3 2,2 ]], заказ 103680 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Усеченный 1 22 многогранник
Строительство
[ редактировать ]Его конструкция основана на группе E 6 , а информацию можно извлечь из кольцевой диаграммы Кокстера-Динкина, представляющей этот многогранник: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Изображения
[ редактировать ]Вершины окрашены в соответствии с их кратностью в этой проекции в прогрессивном порядке: красный, оранжевый, желтый.
| Е6 [12] | Д5 [8] | Д4/А2 [6] | Б6 [12/2] |
|---|---|---|---|
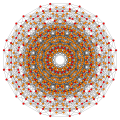 |  | 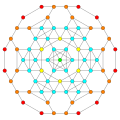 |  |
| А5 [6] | A4 [5] | А3/Д3 [4] | |
 |  |  |
Биректифицированный 1 22 многогранник
[ редактировать ]| Биректифицированный 1 22 многогранник | |
|---|---|
| Тип | Равномерный 6-многогранник |
| Символ Шлефли | 2р{3,3 2,2 } |
| Символ Коксетера | 2р(1 22 ) |
| Диаграмма Кокстера-Динкина | или |
| 5-гранный | 126 |
| 4-ликий | 2286 |
| Клетки | 10800 |
| Лица | 19440 |
| Края | 12960 |
| Вершины | 2160 |
| Вершинная фигура | |
| Группа Коксетера | Е 6 , [[3,3 2,2 ]], заказ 103680 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Двукантеллированный 2 21
- Биректифицированный пентаконтитетрапетон (барм) (Джонатан Бауэрс) [9]
Изображения
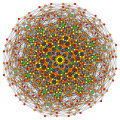
[ редактировать ]Вершины окрашены в соответствии с их кратностью в этой проекции в прогрессивном порядке: красный, оранжевый, желтый.
| Е6 [12] | Д5 [8] | Д4/А2 [6] | Б6 [12/2] |
|---|---|---|---|
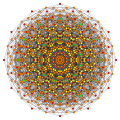 |  | 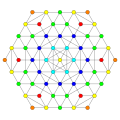 |  |
| А5 [6] | A4 [5] | А3/Д3 [4] | |
 | 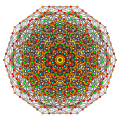 | 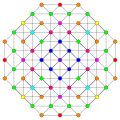 |
1 22 Триректифицированный многогранник
[ редактировать ]| 1 22 Триректифицированный многогранник | |
|---|---|
| Тип | Равномерный 6-многогранник |
| Символ Шлефли | 3р{3,3 2,2 } |
| Символ Коксетера | 3р(1 22 ) |
| Диаграмма Кокстера-Динкина | или |
| 5-гранный | 558 |
| 4-ликий | 4608 |
| Клетки | 8640 |
| Лица | 6480 |
| Края | 2160 |
| Вершины | 270 |
| Вершинная фигура | |
| Группа Коксетера | Е 6 , [[3,3 2,2 ]], заказ 103680 |
| Характеристики | выпуклый |
Альтернативные названия
[ редактировать ]- Треугольный 2 21
- Триректифицированный пентаконтитетрапетон (трим или какам) (Джонатан Бауэрс) [10]
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Эльте, 1912 г.
- ^ Клитцинг, (o3o3o3o3o *c3x - mo )
- ^ Коксетер, Правильные многогранники, 11.8 Фигуры Госсета в шести, семи и восьми измерениях, с. 202-203
- ^ Коксетер, HSM, Правильные комплексные многогранники , второе издание, Cambridge University Press, (1991). стр.30 и стр.47
- ^ Ячейки Вороного решеток E6 * и E7 *. Архивировано 30 января 2016 г. в Wayback Machine , Эдвард Первин.
- ^ Клитцинг, (o3o3x3o3o *c3o - баран )
- ^ Коксетер, Правильные многогранники, 11.8 Фигуры Госсета в шести, семи и восьми измерениях, с. 202-203
- ^ Клитцинг, Ричард. «6D выпуклый равномерный полипет o3o3x3o3o *c3o - баран» .
- ^ Клитцинг, (o3x3o3x3o *c3o - грудь )
- ^ Клитцинг, (x3o3o3o3x *c3o - cacam
Ссылки
[ редактировать ]- Эльте, EL (1912), Полуправильные многогранники гиперпространств , Гронинген: Гронингенский университет.
- HSM Coxeter , Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45] См. стр. 334 (рисунок 3.6a) Питера МакМаллена: (12-угольный граф узлов и ребер из 1 22 )
- Клитцинг, Ричард. «6D однородные многогранники (полипеты)» . o3o3o3o3o *c3x - мо, o3o3x3o3o *c3o - баран, o3x3o3x3o *c3o - барм








