3-3 дуопризма
| 3-3 дуопризма | |
|---|---|
 3D-перспективная проекция с двумя разными поворотами | |
| Тип | Равномерная дуопризма |
| Символ Шлефли | {3}×{3} = {3} 2 |
| Диаграмма Кокстера | |
| Двойной | 3-3 дуопирамиды |
| Характеристики | выпуклый , вершинно-однородный , фасетно-транзитивный |
В геометрии 4-х измерений дуопризма 3-3 или треугольная дуопризма представляет собой четырёхмерный выпуклый многогранник . Его можно построить как декартово произведение двух треугольников, и он является простейшим из бесконечного семейства четырехмерных многогранников, построенных как декартово произведение двух многоугольников, дуопризм .
Он имеет 9 вершин, 18 ребер, 15 граней (9 квадратов и 6 треугольников ), в 6 треугольной призмы ячейках . Есть диаграмма Кокстера. ![]()
![]()
![]() и симметрия [[3,2,3]], порядка 72. Его вершины и ребра образуют ладейный граф .
и симметрия [[3,2,3]], порядка 72. Его вершины и ребра образуют ладейный граф .
Описание
[ редактировать ]Дуопризма — это 4-многогранник, который можно построить с помощью декартова произведения двух многоугольников. [1] В случае 3-3 дуопризма является самой простой среди них, и ее можно построить, используя декартово произведение двух треугольников. Получившаяся дуопризма имеет 9 вершин, 18 ребер, [2] и 15 граней, в том числе 9 квадратов и 6 треугольников. Его ячейка имеет 6 треугольных призм .
Гиперобъем ребра однородной 3-3-дуопризмы с длиной является Это квадрат площади равностороннего треугольника ,
Дуопризму 3-3 можно представить в виде графа, имеющего одинаковое количество вершин и ребер. Подобно графу Берлекампа-ван Линта-Зейделя и неизвестному решению проблемы 99-графов Конвея , каждое ребро является частью уникального треугольника, а каждая несмежная пара вершин является диагональю уникального квадрата. Это тороидальный граф , локально линейный граф , сильно регулярный граф с параметрами (9,4,1,2), ладейный граф и граф Пэли порядка 9. [3] Этот граф также является графом Кэли группы с генераторной установкой .
Симметрия
[ редактировать ]В 5-мерном измерении некоторые однородные 5-многогранники имеют 3-3 вершинные фигуры дуопризмы , некоторые с неравной длиной ребер и, следовательно, более низкой симметрией:
| Симметрия | [[3,2,3]], порядок 72 | [3,2], порядок 12 | ||
|---|---|---|---|---|
| Коксетер диаграмма | ||||
| Шлегель диаграмма | 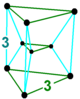 |  |  | 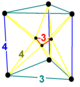 |
| Имя | т 2 а 5 | т 03 а 5 | т 03 γ 5 | т 03 β 5 |
Биректифицированные 16-ячеистые соты также имеют вершинную фигуру дуопризмы 3-3 . Существуют три конструкции сот с двумя нижними симметриями.
| Симметрия | [3,2,3], порядок 36 | [3,2], порядок 12 | [3], порядок 6 |
|---|---|---|---|
| Коксетер диаграмма | |||
| Перекос ортогональный проекция |  |  | 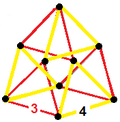 |
Связанные сложные многоугольники
[ редактировать ]Правильный комплексный многогранник 3 {4} 2 , ![]()
![]()
![]() , в имеет реальное представление в виде 3-3- дуопризмы в 4-мерном пространстве. 3 {4} 2 имеет 9 вершин и 6 3-рёбер. Его симметрия равна 3 [4] 2 , порядок 18. Он также имеет конструкцию более низкой симметрии,
, в имеет реальное представление в виде 3-3- дуопризмы в 4-мерном пространстве. 3 {4} 2 имеет 9 вершин и 6 3-рёбер. Его симметрия равна 3 [4] 2 , порядок 18. Он также имеет конструкцию более низкой симметрии, ![]()
![]()
![]() , или 3 {}× 3 {}, с симметрией 3 [2] 3 , порядок 9. Это симметрия, если красные и синие 3-ребра считаются различными. [4]
, или 3 {}× 3 {}, с симметрией 3 [2] 3 , порядок 9. Это симметрия, если красные и синие 3-ребра считаются различными. [4]
 Перспективная проекция |  Ортогональная проекция с совпадающими центральными вершинами | 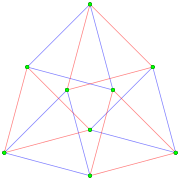 Ортогональная проекция, вид со смещением, чтобы избежать перекрытия элементов. |
Связанные многогранники
[ редактировать ]| Космос | Конечный | евклидов | гиперболический | ||
|---|---|---|---|---|---|
| н | 4 | 5 | 6 | 7 | 8 |
| Коксетер группа | А 2 А 2 | EЕ6 | = Е 6 + | = Е 6 ++ | |
| Коксетер диаграмма | |||||
| Симметрия | [[3 2,2,-1 ]] | [[3 2,2,0 ]] | [[3 2,2,1 ]] | [[3 2,2,2 ]] | [[3 2,2,3 ]] |
| Заказ | 72 | 1440 | 103,680 | ∞ | |
| График |  |  |  | ∞ | ∞ |
| Имя | −1 22 | 0 22 | 1 22 | 2 22 | 3 22 |
3-3 дуопирамиды
[ редактировать ]| 3-3 дуопирамиды | |
|---|---|
| Тип | Единая двойная дуопирамида |
| Символ Шлефли | {3}+{3} = 2{3} |
| Диаграмма Кокстера | |
| Клетки | 9 тетрагональных дисфеноидов |
| Лица | 18 равнобедренных треугольников |
| Края | 15 (9+6) |
| Вершины | 6 (3+3) |
| Симметрия | [[3,2,3]] = [6,2 + ,6], порядок 72 |
| Двойной | 3-3 дуопризма |
| Характеристики | выпуклый , вершинно-однородный , фасетно-транзитивный |
Двойная дуопризма 3-3 называется 3-3 дуопирамидой или треугольной дуопирамидой . Он имеет 9 тетрагональных дисфеноидных ячеек, 18 треугольных граней, 15 ребер и 6 вершин.
В ортогональной проекции его можно увидеть как 6-угольный круг вершин и ребер, соединяющих все пары, как 5-симплекс, видимый в проекции.
Связанный сложный многоугольник
[ редактировать ]Правильный комплексный многоугольник 2 {4} 3 , а также 3 { }+ 3 { } имеет 6 вершин в с реальным представительством в соответствующие такому же расположению вершин дуопирамиды 3-3. Он имеет 9 2-ребер, соответствующих соединительным ребрам 3-3-дуопирамиды, при этом 6 рёбер, соединяющих два треугольника, не включены. Его можно увидеть в шестиугольной проекции с тремя наборами цветных краев. Такое расположение вершин и ребер образует полный двудольный граф , в котором каждая вершина одного треугольника соединена с каждой вершиной другого. Его также называют графом Томсена или 4- клеткой . [5]
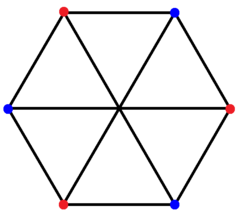 2 полный {4} 3 с 6 вершинами синего и красного цвета, соединенными 9 2-ребрами, образующими двудольный граф . | 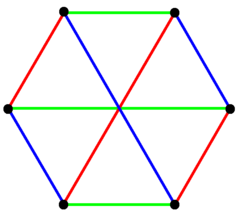 Он имеет 3 набора по 3 края, которые можно увидеть здесь в цветах. |
См. также
[ редактировать ]- 3-4 дуопризмы
- Тессеракт (4-4 дуопризмы)
- 5-5 дуопризма
- Выпуклый правильный 4-многогранник
- Дуоцилиндр
Ссылки
[ редактировать ]- ^ Коксетер, HSM (1948), Правильные многогранники , Methuen & Co. Ltd., Лондон, стр. 124
- ^ Ли, Жуймин; Яо, Ян-Ань (2016), «Реверсивный механизм дуопризмы», Frontiers of Machine Engineering , 11 : 159–169, doi : 10.1007/s11465-016-0398-6
- ^ Махнев А.А.; Минакова И.М. (январь 2004 г.), "Об автоморфизмах сильно регулярных графов с параметрами , ", Дискретная математика и приложения , 14 (2), doi : 10.1515/156939204872374 , MR 2069991 , S2CID 118034273
- ^ Коксетер, HSM ; Регулярные комплексные многогранники , издательство Кембриджского университета, (1974).
- ^ Правильные комплексные многогранники, стр.110, стр.114
- Коксетер , Красота геометрии: двенадцать эссе , Dover Publications, 1999, ISBN 0-486-40919-8 (Глава 5: Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги)
- Коксетер, HSM Правильные косые многогранники в трех и четырех измерениях. Учеб. Лондонская математика. Соц. 43, 33–62, 1937.
- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (глава 26)
- Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
- Каталог Выпуклой Полихоры, раздел 6 , Георгий Ольшевский.
- Упаковки аполлоновых шаров и сложенные многогранники. Дискретная и вычислительная геометрия, июнь 2016 г., том 55, выпуск 4, стр. 801–826.
Внешние ссылки
[ редактировать ]- В книге «Четвертое измерение просто объяснено» дуопризмы описываются как «двойные призмы», а дуоцилиндры - как «двойные цилиндры».
- Polygloss - глоссарий многомерных терминов
- Исследование гиперпространства с помощью геометрического произведения












