Дуопирамида

В геометрии четырех измерений и выше двойная пирамида , дуопирамида или слиток — это многогранник, построенный из двух ортогональных многогранников с ребрами , соединяющими все пары вершин между ними. Термин «фузиль» используется Норманом Джонсоном как ромбовидная форма. Термин дуопирамида Георгием Ольшевским как двойник дуопризмы . был использован

Многоугольные формы

Набор двойных унифицированных дуопирамид pq
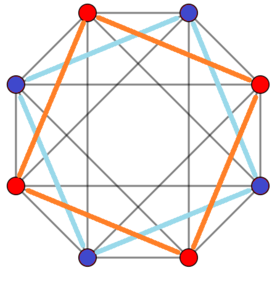Пример 4-4 дуопирамиды (16 ячеек) Ортогональная проекция
Тип	Равномерный двойной полихорон
Символ Шлефли	{р} + {д}
Диаграмма Кокстера
Клетки	pq двуугольные дисфеноиды
Лица	2pq треугольники
Края	pq+p+q
Вершины	р+q
Вершинные фигуры	p-угольная бипирамида q-угольная бипирамида
Симметрия	[p,2,q], порядок 4pq
Двойной	pq- дуопризма
Характеристики	выпуклый , фасетно-транзитивный
Набор двойных однородных дуопирамид из полипропилена
Символ Шлефли	{p} + {p} = 2{p}
Диаграмма Кокстера
Клетки	п 2 тетрагональные дисфеноиды
Лица	2р 2 треугольники
Края	п 2 +2р
Вершины	2р
Вершинная фигура	p-угольная бипирамида
Симметрия	[[p,2,p]] = [2p,2 + ,2п], порядок 8п 2
Двойной	ПП дуопризма
Характеристики	выпуклый , фасетно-транзитивный

Формы низшей размерности четырехмерны и соединяют два многоугольника. Дуопирамида p - q {p} + { или p - q fusil , представленная составным символом Шлефли q}, и диаграммой Коксетера-Дынкина . Обычную 16-клеточную структуру можно рассматривать как дуопирамиду 4-4 или 4-4 слитка. , симметрия [[4,2,4]], порядок 128.

Дуопирамида pq или pq fusil имеет группы Кокстера симметрию [ p ,2, q ], порядка 4pq. Когда p и q идентичны, симметрия в обозначениях Кокстера удваивается как [[ p ,2, p ]] или [2 p ,2 ⁺ ,2 q ], порядок 8 p ² .

Ребра существуют во всех парах вершин между p -угольником и q -угольником. дуопирамиды 1-скелет p - q представляет собой ребра каждого многоугольника p и q и pq полный двудольный граф между ними.

Геометрия

Дуопирамиду p - q можно рассматривать как два правильных плоских многоугольника со сторонами p и q с одинаковым центром и ортогональными ориентациями в четырех измерениях. Наряду с ребрами p и q двух многоугольников все перестановки вершин одного многоугольника в вершины другого образуют ребра. Все грани треугольные: одно ребро одного многоугольника соединено с одной вершиной другого многоугольника. Многоугольники с p и q сторонами являются полыми , проходят через центр многогранника и не определяют грани. Ячейки представляют собой тетраэдры, построенные как все перестановки пар ребер между каждым многоугольником.

Это можно понять по аналогии с отношением трехмерных призм и их двойственных бипирамид с символом Шлефли { } + { p } и ромбом в 2D как { } + { }. Бипирамиду можно рассматривать как трехмерную вырожденную дуопирамиду, добавив ребро через двуугольник { } на внутренней оси и добавив пересекающиеся внутренние треугольники и тетраэдры, соединяющие это новое ребро с вершинами и ребрами p-угольника.

Другие неоднородные полихоры можно назвать дуопирамидами по той же конструкции, что и два ортогональных и соцентрированных многоугольника, соединенных ребрами со всеми комбинациями пар вершин между многоугольниками. Симметрия будет произведением симметрии двух многоугольников. Таким образом, дуопирамида прямоугольник-прямоугольник будет топологически идентична однородной дуопирамиде 4-4 , но более низкая симметрия [2,2,2], порядка 16, возможно, удвоится до 32, если два прямоугольника идентичны.

Координаты дуопирамиды pq (на единичной 3-сфере ) могут быть заданы как:

$(\cos {\frac {2\pi i}{p}},\sin {\frac {2\pi i}{p}},0,0),\quad i=1\dots p$

$(0,0,\cos {\frac {2\pi j}{q}},\sin {\frac {2\pi j}{q}}),\quad j=1\dots q$

Все пары вершин соединены ребрами.

Перспективные прогнозы

3-3	3-4	4-4 (16-ячеечный)

Ортогональные проекции

2n вершин nn-дуопирамиды можно ортогонально спроектировать в два правильных n-угольника с ребрами между всеми вершинами каждого n-угольника.

Обычную 16-клеточную пирамиду можно рассматривать как дуопирамиду 4-4 , двойственную дуопризме 4-4 , которая является тессерактом . В дуопирамиде 4-4 симметрия 16-ячеечной симметрии равна [4,2,4], порядка 64 и удвоена до [[4,2,4]], порядка 128 с двумя взаимозаменяемыми центральными квадратами. Обычная 16-ячеечная имеет более высокую симметрию [3,3,4], порядок 384.

ПП дуопирамиды

3-3	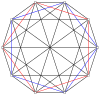5-5	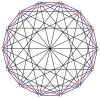7-7	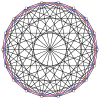9-9	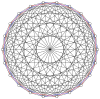11-11	13-13	15-15	17-17	19-19
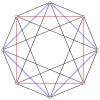4-4 ( 16-ячеечный )	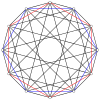6-6	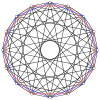8-8	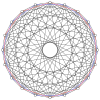10-10	12-12	14-14	16-16	18-18	20-20

pq дуопирамиды

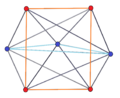3-4	3-5	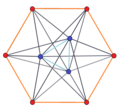3-6	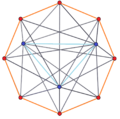3-8
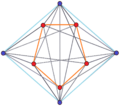4-5	4-6

Пример 6-4 дуопирамиды

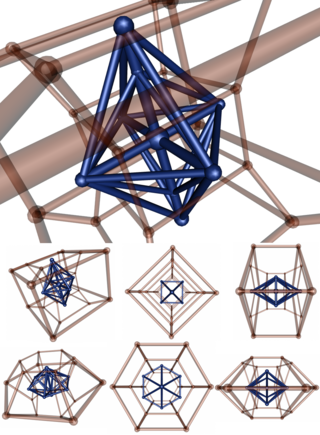Это вершинно-центрированная стереографическая проекция дуопирамиды 6-4 (синего цвета) с двойной дуопризмой (прозрачно-красного цвета). В последнем ряду дуопирамида проецируется направлением, перпендикулярным первому; поэтому два параметра (6,4), кажется, поменялись местами. Действительно, асимметрия возникает из-за проекции: два параметра симметричны в 4D.