Икосаэдрический 120-ячеечный
| Икосаэдрический 120-ячеечный | |
|---|---|
 Ортогональная проекция | |
| Тип | Многогранники Шлефли-Гесса |
| Клетки | 120 {3,5} |
| Лица | 1200 {3} |
| Края | 720 |
| Вершины | 120 |
| Вершинная фигура | {5,5/2} |
| Символ Шлефли | {3,5,5/2} |
| Группа симметрии | Ч 4 , [3,3,5] |
| Диаграмма Кокстера-Динкина |       |
| Двойной | Маленький звездчатый, 120 ячеек. |
| Характеристики | Обычный |
В геометрии икосаэдр из 120 ячеек , полиикосаэдр , ограненный из 600 ячеек или икосаплекс представляет собой правильный звездчатый 4-многогранник с символом Шлефли {3,5,5/2}. Это один из 10 правильных многогранников Шлефли-Гесса .
Он построен пятью икосаэдрами вокруг каждого ребра пентаграммной фигуры. Вершинная фигура представляет собой большой додекаэдр .
Связанные многогранники
[ редактировать ]Он имеет то же расположение ребер , что и 600-ячеечный , большой 120-ячеечный и большой 120-ячеечный , и разделяет свои вершины со всеми другими 4-многогранниками Шлефли-Гесса , за исключением большого большого звездчатого 120-ячеечного многогранника (еще одна звездочка из 120-ячеечного многогранника). клетка ).
| Ч 4 | - | FF4 |
|---|---|---|
 [30] | 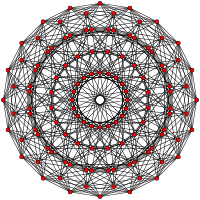 [20] |  [12] |
| HH3 | А 2 / Б 3 / Д 4 | А3 / Б2 |
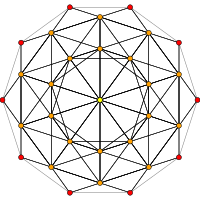 [10] |  [6] | 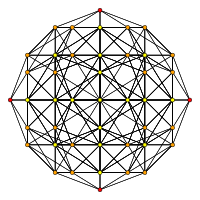 [4] |
Как ограненный 600-ячеечный, заменяющий симплициальные ячейки 600-ячеечного икосаэдрическими пятиугольными многогранными ячейками, его можно рассматривать как четырехмерный аналог большого додекаэдра , который заменяет треугольные грани икосаэдра пятиугольными гранями. Действительно, икосаэдр со 120 ячейками двойственен маленькому звездчатому 120 ячейкам , который можно рассматривать как 4D аналог малого звездчатого додекаэдра , двойственного большому додекаэдру.
См. также
[ редактировать ]- Список правильных многогранников
- Выпуклый правильный 4-многогранник
- Тела Кеплера-Пуансо - правильный звездчатый многогранник.
- Звездчатый многоугольник - правильные звездчатые многоугольники.
Ссылки
[ редактировать ]- Эдмунд Гесс , (1883) Введение в теорию сферического деления со специальным рассмотрением ее применения к теории равноповерхностей и равноугольных многогранников [1] .
- HSM Coxeter , Правильные многогранники , 3-е. изд., Dover Publications, 1973. ISBN 0-486-61480-8 .
- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26, Правильные звездчатые многогранники, стр. 404–408)
- Клитцинг, Ричард. "4D однородные многогранники (полихора) x3o5o5/2o - исправить" .
Внешние ссылки
[ редактировать ]- Обычная полихора. Архивировано 6 сентября 2003 г. в Wayback Machine.
- Дискуссия об именах
- Правильные многогранники
- Обычная звездная полихора
 | Эта из 4-х многогранников статья незавершена . Вы можете помочь Википедии, расширив ее . |