Многогранник Кеплера – Пуансо

Большой додекаэдр

Малый звездчатый додекаэдр

Большой икосаэдр

Большой звездчатый додекаэдр

В геометрии многогранник Кеплера -Пуансо — это любой из четырех правильных звездчатых многогранников .

Они могут быть получены путем звездообразования правильного выпуклого додекаэдра и икосаэдра и отличаются от них наличием правильных пентаграммных граней или вершинных фигур . Всех их так или иначе можно рассматривать как трехмерные аналоги пентаграммы.

Характеристики

Размеры

Длина ребра большого икосаэдра равна $\phi ^{4}={\tfrac {1}{2}}{\bigl (}7+3{\sqrt {5}}\,{\bigr )}$ раз больше длины исходного ребра икосаэдра.Длины ребер малого звездчатого додекаэдра, большого додекаэдра и большого звездчатого додекаэдра равны соответственно $\phi ^{3}=2+{\sqrt {5}},$ $\phi ^{2}={\tfrac {1}{2}}{\bigl (}3+{\sqrt {5}}\,{\bigr )},$ и $\phi ^{5}={\tfrac {1}{2}}{\bigl (}11+5{\sqrt {5}}\,{\bigr )}$ раз больше длины исходного ребра додекаэдра.

Невыпуклость

Эти фигуры имеют пентаграммы (звездные пятиугольники) в качестве граней или фигур вершин. Малый большой и звездчатый додекаэдр имеют невыпуклые правильные грани пентаграммы . Большой додекаэдр и большой икосаэдр имеют выпуклые многоугольные грани, но вершинные фигуры — пентаграммы .

Во всех случаях две грани могут пересекаться по линии, не являющейся краем ни одной из граней, так что часть каждой грани проходит через внутреннюю часть фигуры. Такие линии пересечения не являются частью многогранной структуры и иногда называются ложными ребрами. Аналогично, если три такие линии пересекаются в точке, не являющейся углом какой-либо грани, эти точки являются ложными вершинами. На изображениях ниже показаны сферы в истинных вершинах и синие стержни вдоль истинных ребер.

Например, маленький звездчатый додекаэдр имеет 12 граней -пентаграмм , центральная пятиугольная часть которых скрыта внутри тела. Видимые части каждой грани состоят из пяти равнобедренных треугольников , соприкасающихся в пяти точках вокруг пятиугольника. Мы могли бы рассматривать эти треугольники как 60 отдельных граней и получить новый неправильный многогранник, внешне идентичный. Каждое ребро теперь будет разделено на три более коротких ребра (двух разных типов), а 20 ложных вершин станут истинными, так что всего у нас будет 32 вершины (опять двух видов). Скрытые внутренние пятиугольники больше не являются частью поверхности многогранника и могут исчезнуть. Теперь формула Эйлера справедлива: 60 ​​− 90 + 32 = 2. Однако этот многогранник больше не является тем, который описывается символом Шлефли {5/2, 5}, и поэтому не может быть телом Кеплера – Пуансо, хотя он по-прежнему выглядит как будто снаружи.

Эйлерова характеристика χ

Многогранник Кеплера-Пуансо покрывает свою описанную сферу более одного раза, при этом центры граней действуют как точки извилины в фигурах с пентаграммными гранями, а вершины - в других. Из-за этого они не обязательно топологически эквивалентны сфере, как платоновы тела, и, в частности, соотношение Эйлера.

$\chi =V-E+F=2\$

не всегда держится. Шлефли считал, что все многогранники должны иметь χ = 2, и отверг малый звездчатый додекаэдр и большой додекаэдр как собственные многогранники. Эта точка зрения никогда не была широко распространена.

Модифицированная форма формулы Эйлера, использующая плотность ( D ) фигур вершин ( $d_{v}$) и лица ( $d_{f}$) было дано Артуром Кэли и справедливо как для выпуклых многогранников (где все поправочные коэффициенты равны 1), так и для многогранников Кеплера – Пуансо:

$d_{v}V-E+d_{f}F=2D.$

Дуальность и многоугольники Петри

Многогранники Кеплера–Пуансо существуют в дуальных парах. Дуалы имеют один и тот же многоугольник Петри , а точнее, многоугольники Петри с одинаковой двумерной проекцией.

На следующих изображениях показаны два двойных соединения с одинаковым радиусом кромки . Они также показывают, что полигоны Петри перекошены .На изображениях также легко увидеть две зависимости, описанные в статье ниже: то, что фиолетовые края одинаковы, и что зеленые грани лежат в одних и тех же плоскостях.

горизонтальный край спереди	вертикальный край спереди	Полигон Петри
маленький звездчатый додекаэдр $\left\{{\frac {5}{2}},5\right\}$	большой додекаэдр $\left\{5,{\frac {5}{2}}\right\}$	шестиугольник $\left\{{\frac {6}{1,3}}\right\}$
большой икосаэдр $\left\{3,{\frac {5}{2}}\right\}$	большой звездчатый додекаэдр $\left\{{\frac {5}{2}},3\right\}$	декаграмма $\left\{{\frac {10}{3,5}}\right\}$

Соединение SD и GD с шестиугольниками Петри

Соединение gI и gsD с декаграммами Петри

Краткое содержание

Имя (аббревиатура Конвея)	Картина	сферический плитка	Звездчатость диаграмма	Шлефли {p, q} и Коксетер-Дынкин	Лица {р}	Края	Вершины {д}	Вертекс фигура (конфигурация)	Полигон Петри	час	Плотность	Симметрия	Двойной
большой додекаэдр (гД)				{5, 5/2}	12 {5}	30	12 {5/2}	(5 5 )/2	{6}	−6	3	I h	маленький звездчатый додекаэдр
маленький звездчатый додекаэдр (СД)				{5/2, 5}	12 {5/2}	30	12 {5}	(5/2) 5	{6}	−6	3	I h	большой додекаэдр
большой икосаэдр (ги)				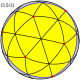{3, 5/2}	20 {3}	30	12 {5/2}	(3 5 )/2	{10/3}	2	7	I h	большой звездчатый додекаэдр
большой звездчатый додекаэдр (сгД = гсД)				{5/2, 3}	12 {5/2}	30	20 {3}	(5/2) 3	{10/3}	2	7	I h	большой икосаэдр

Отношения между правильными многогранниками

Система отношений Конвея между шестью многогранниками (упорядоченными по вертикали по плотности )

Операционная терминология Конвея

Джон Конвей определяет многогранники Кеплера-Пуансо как увеличения и звездчатые тела выпуклых тел.
В его соглашении об именах маленький звездчатый додекаэдр — это просто звездчатый додекаэдр .

икосаэдр (I)	додекаэдр (D)
большой додекаэдр (gD)	звездчатый додекаэдр (sD)
большой икосаэдр (gI)	большой звездчатый додекаэдр (sgD = gsD)

Звездчатость превращает пятиугольные грани в пентаграммы. (В этом смысле звездообразование является уникальной операцией, и ее не следует путать с более общим созвездием, описанным ниже.)

Greatening сохраняет тип граней, сдвигая и изменяя их размеры в параллельные плоскости.

showПроиллюстрированы отношения Конвея
diagram	The polyhedra in this section are shown with the same midradius.
stellation	D sD gD sgD = gsD
greatening	D and gD I and gI sD and gsD
duality	D and I gD and sD gI and gsD

Звездочки и огранки

Большой икосаэдр одна из звёздочек икосаэдра . — (См. «Пятьдесят девять икосаэдров »).
Все три других — это звездочки додекаэдра .

Большой звездчатый додекаэдр — это огранка додекаэдра.
Три других являются гранями икосаэдра.

showЗвездочки и огранки
Convex	icosahedron			dodecahedron
Stellations	gI (the one with yellow faces)			gD	sD	gsD
Facetings	gI	gD	sD	gsD (the one with yellow vertices)

Если пересечения рассматривать как новые ребра и вершины, полученные фигуры не будут правильными , но их все равно можно считать звездочками .

(См. также Список моделей многогранников Веннингера )

Общие вершины и ребра

Большой звездчатый додекаэдр имеет общие вершины с додекаэдром. Остальные три многогранника Кеплера-Пуансо имеют общий с икосаэдром. Скелеты топологически тел, имеющих общие вершины, эквивалентны .

икосаэдр	большой додекаэдр	большой икосаэдр	маленький звездчатый додекаэдр	додекаэдр	большой звездчатый додекаэдр
делиться вершинами и ребрами		делиться вершинами и ребрами		общие вершины и скелеты образуют додекаэдрический граф
общие вершины, скелеты образуют икосаэдрический граф

Звездчатые додекаэдры

Корпус и ядро

Малый большой и звездчатый додекаэдр.можно рассматривать как правильный и большой додекаэдр , ребра и грани которого вытянуты до пересечения.
Пятиугольные грани этих ядер являются невидимыми частями граней пентаграмм звездных многогранников.
Для малого звездчатого додекаэдра оболочка равна $\varphi$ раз больше ядра, и для великих это $\varphi +1=\varphi ^{2}$ раз больше. (См. Золотое сечение )
( Средний радиус — это общепринятая мера для сравнения размеров различных многогранников.)

showОболочка и ядро ​​звездчатых додекаэдров
Hull	Star polyhedron	Core	${\frac {\text{hull midradius}}{\text{core midradius}}}$	${\frac {\text{core midradius}}{\text{hull midradius}}}$
			${\frac {{\sqrt {5}}+1}{2}}=1.61803...$	${\frac {{\sqrt {5}}-1}{2}}=0.61803...$
			${\frac {3+{\sqrt {5}}}{2}}=2.61803...$	${\frac {3-{\sqrt {5}}}{2}}=0.38196...$
The platonic hulls in these images have the same midradius. This implies that the pentagrams have the same size, and that the cores have the same edge length. (Compare the 5-fold orthographic projections below.)

Аугментации

Традиционно два звездчатых многогранника определялись как приращения (или кумуляции ). т.е. как додекаэдр и икосаэдр с добавленными к их граням пирамидами.

Кеплер называет маленькую звездочку увеличенным додекаэдром (затем прозвав ее ежом ).

По его мнению, большая звездочка связана с икосаэдром, как малая — с додекаэдром.

Эти наивные определения используются до сих пор.Например, MathWorld утверждает, что два звездчатых многогранника можно построить путем добавления пирамид к граням Платоновых тел.

Это всего лишь помощь для визуализации формы этих тел, а не утверждение, что пересечения ребер (ложные вершины) являются вершинами. Если бы это было так, два звездчатых многогранника были бы топологически эквивалентны пентакисдодекаэдру и триакису икосаэдру .

showЗвездчатые додекаэдры как дополнения
Core	Star polyhedron	Catalan solid

Симметрия

Все многогранники Кеплера-Пуансо обладают полной икосаэдрической симметрией , как и их выпуклые оболочки.

Большой икосаэдр и его двойник напоминают икосаэдр и его двойник тем, что у них есть грани и вершины на осях симметрии 3-го (желтого) и 5-го порядка (красного).
В большом додекаэдре и его двойнике все грани и вершины лежат на осях симметрии 5-го порядка (поэтому на этих изображениях нет желтых элементов).

В следующей таблице показаны твердые тела в парах двойников. В верхнем ряду они показаны с пиритоэдрической симметрией , в нижнем ряду с икосаэдрической симметрией (к которой относятся указанные цвета).

В таблице ниже показаны ортогональные проекции от осей симметрии 5-го (красного), 3-го (желтого) и 2-го (синего) порядка.

{3, 5} ( I ) и {5, 3} ( D )	{5, 5/2} ( gD ) и {5/2, 5} ( sD )	{3, 5/2} ( gI ) ​​и {5/2, 3} ( gsD )
( анимации )	( анимации )	( анимации )
( анимации )	( анимации )	( анимации )

showорфографические проекции
The platonic hulls in these images have the same midradius, so all the 5-fold projections below are in a decagon of the same size.(Compare projection of the compound.)This implies that sD, gsD and gI have the same edge length,namely the side length of a pentagram in the surrounding decagon.

История

Большинство, если не все, многогранников Кеплера-Пуансо были известны в той или иной форме до Кеплера. Небольшой звездчатый додекаэдр появляется в мраморной инкрустации (панели) на полу базилики Святого Марка , в Венеции Италия. Он датируется 15 веком и иногда приписывается Паоло Уччелло .

В своей книге Perspectiva Corporum Regularium ( «Перспективы правильных тел» ), книге гравюр на дереве, опубликованной в 1568 году, Венцель Ямницер изображает большой звездчатый додекаэдр и большой додекаэдр (оба показаны ниже). Существует также усеченная версия малого звездчатого додекаэдра . Из общей структуры книги ясно, что он считал правильными только пять Платоновых тел.

Малый и большой звездчатые додекаэдры, иногда называемые многогранниками Кеплера , были впервые признаны правильными Иоганном Кеплером около 1619 года. Он получил их, образуя звездчатку правильного выпуклого додекаэдра, впервые рассматривая его как поверхность, а не как твердое тело. Он заметил, что, удлиняя края или грани выпуклого додекаэдра до тех пор, пока они снова не встретятся, он может получить звездные пятиугольники. Кроме того, он признал, что эти звездные пятиугольники также являются правильными. Таким образом он построил два звездчатых додекаэдра. У каждого есть центральная выпуклая область каждого лица, «скрытая» внутри, и видны только треугольные руки. Последним шагом Кеплера было признание того, что эти многогранники соответствуют определению регулярности, хотя они и не были выпуклыми , как традиционные платоновы тела .

В 1809 году Луи Пуансо заново открыл фигуры Кеплера, соединив вокруг каждой вершины звездные пятиугольники. Он также собрал выпуклые многоугольники вокруг вершин звезд, чтобы открыть еще две правильные звезды: большой икосаэдр и большой додекаэдр. Некоторые люди называют эти два многогранника Пуансо . Пуансо не знал, открыл ли он все правильные звездчатые многогранники.

Три года спустя Огюстен Коши доказал полноту списка, расставив звездчатые тела Платона , а почти полвека спустя, в 1858 году, Бертран предоставил более элегантное доказательство, разграничив их.

В следующем году Артур Кэли дал многогранникам Кеплера-Пуансо названия, под которыми они широко известны сегодня.

Сто лет спустя Джон Конвей разработал систематическую терминологию для созвездий в четырех измерениях. В рамках этой схемы малый звездчатый додекаэдр — это просто звездчатый додекаэдр .

Напольная мозаика в Святого Марка соборе в Венеции (возможно, Паоло Уччелло )

Большой додекаэдр и большой звездчатый додекаэдр в перспективе правильных тел (1568 г.)

Звездчатые додекаэдры, Harmonices Mundi работы Иоганна Кеплера (1619 г.)

Картонная модель большого икосаэдра из Тюбингенского университета (около 1860 г.)

Правильные звездчатые многогранники в искусстве и культуре

Звезда Александра

Правильные звездчатые многогранники впервые появляются в искусстве эпохи Возрождения. Небольшой звездчатый додекаэдр изображен в мраморной интарсии на полу базилики Святого Марка в Венеции, Италия, датируемой ок. 1430 г. и иногда приписывают Пауло Уччелло .

В 20 веке художника М. К. Эшера интерес к геометрическим формам часто приводил к созданию работ, основанных на правильных твердых телах или включающих их; В основе гравитации лежит небольшой звездчатый додекаэдр.

Разрез х большого додекаэдра был использован в головоломке «Звезда Александра» 1980- годов .

норвежского художника Вебьёрна Санда Скульптура «Звезда Кеплера» выставлена ​​возле аэропорта Осло Гардермуэн . Размер звезды составляет 14 метров, она состоит из икосаэдра и додекаэдра внутри большого звездчатого додекаэдра.

См. также

• Правильный многогранник
• Правильный многогранник
• Список правильных многогранников
• Однородный многогранник
• Однородный звездчатый многогранник
• Полиэдрическое соединение
• Правильный звездный 4-многогранник - десять правильных звездных 4-многогранников , 4-мерные аналоги многогранников Кеплера – Пуансо.

Ссылки

Библиография

• Ж. Бертран , Заметки о теории правильных многогранников, Отчеты сессий Академии наук , 46 (1858), стр. 79–82, 117.
• Огюстен-Луи Коши , Исследование многогранников. Ж. де л'Эколь Политехническая школа 9, 68–86, 1813.
• Артур Кэли , О четырех новых правильных телах Пуансо. Фил. Маг. 17 , стр. 123–127 и 209, 1859 г.
• Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус , Симметрия вещей 2008, ISBN   978-1-56881-220-5 (Глава 24, Правильные звездчатые многогранники, стр. 404–408)
• Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
  • (Документ 1) HSM Coxeter, Девять правильных тел [Proc. Может. Математика. Конгресс 1 (1947), 252–264, МР 8, 482]
  • (Документ 10) HSM Коксетер, Звездные многогранники и функция Шлафли f(α,β,γ) [Elements of Mathematics 44 (2) (1989) 25–36]
• Теони Паппас , (Тела Кеплера – Пуансо) Радость математики . Сан-Карлос, Калифорния: Wide World Publ./Tetra, с. 113, 1989.
• Луи Пуансо , Мемуары о многоугольниках и многогранниках. Ж. де л'Эколь Политехническая школа 9 , стр. 16–48, 1810.
• Лакатос, Имре; Доказательства и опровержения , Cambridge University Press (1976) - обсуждение доказательства эйлеровой характеристики
• Веннингер, Магнус (1983). Двойные модели . Издательство Кембриджского университета. ISBN  0-521-54325-8 . , стр. 39–41.
• Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус , Симметрии вещей 2008, ISBN   978-1-56881-220-5 (Глава 26. стр. 404: Правильные звездчатые многогранники, измерение 3)
• Энтони Пью (1976). Многогранники: визуальный подход . Калифорния: Издательство Калифорнийского университета в Беркли. ISBN  0-520-03056-7 . Глава 8: Многогранники Кеплера Пуазо

Внешние ссылки

• Вайсштейн, Эрик В. «Тело Кеплера – Пуансо» . Математический мир .
• Бумажные модели многогранников Кеплера – Пуансо.
• Бесплатные бумажные модели (сети) многогранников Кеплера – Пуансо.
• Однородные многогранники
• Твердые тела Кеплера-Пуансо в визуальных многогранниках
• VRML-модели многогранников Кеплера – Пуансо
• Звездчатость и огранка – краткая история
• Stella: Polyhedron Navigator : программное обеспечение, использованное для создания многих изображений на этой странице.