Гранд 600-ячеечный
 | Эта статья включает список литературы , связанную литературу или внешние ссылки , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . ( Май 2023 г. ) |
| Гранд 600-ячеечный | |
|---|---|
 Ортогональная проекция | |
| Тип | Правильный звездчатый 4-многогранник |
| Клетки | 600 {3,3} |
| Лица | 1200 {3} |
| Края | 720 |
| Вершины | 120 |
| Вершинная фигура | {3,5/2} |
| Символ Шлефли | {3,3,5/2} |
| Диаграмма Кокстера-Динкина |       |
| Группа симметрии | Ч 4 , [3,3,5] |
| Двойной | Большой гранд звездчатый, 120 ячеек. |
| Характеристики | Обычный |
В геометрии большой 600-ячеечный или большой политетраэдр представляет собой правильный звездчатый 4-многогранник с символом Шлефли {3, 3, 5/2}. Это один из 10 правильных многогранников Шлефли-Гесса. Он единственный с 600 ячейками.
Это один из четырех правильных звездных 4-многогранников, открытых Людвигом Шлефли . Он был назван Джоном Хортоном Конвеем , расширив систему наименования Артуром Кэли , предложенную тел Кеплера-Пуансо .
Большой 600-ячеечный можно рассматривать как четырехмерный аналог большого икосаэдра (который, в свою очередь, аналогичен пентаграмме ) ; оба они являются единственными правильными n -мерными звездчатыми многогранниками, которые получены путем выполнения звездчатых операций над пятиугольным многогранником , имеющим симплектические грани. Его можно построить аналогично пентаграмме, ее двумерному аналогу, путем расширения упомянутых ( n-1 )-D симплексных граней основного многогранника n D ( тетраэдры для большого 600-ячеечного, равносторонние треугольники для большого икосаэдра , и отрезки линий пентаграммы) до тех пор, пока фигура не приобретет правильные грани.
Большой 600-ячеечный также двойственен большому звездчатому 120-ячеистому , отражая двойственность большого икосаэдра с большим звездчатым додекаэдром (который, в свою очередь, также аналогичен пентаграмме); все это конечные звездочки n -мерного пятиугольного многогранника «додекаэдрического типа».
Связанные многогранники
[ редактировать ]Он имеет то же расположение краев , что и большой звездчатый 120-ячеечный и большой звездчатый 120-ячеечный , а также то же расположение граней, что и большой икосаэдрический 120-ячеечный .
| HH3 | А 2 / Б 3 / Д 4 | А3 / Б2 |
|---|---|---|
 |  |  |
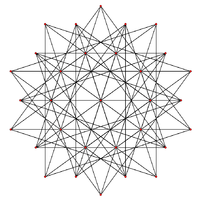См. также
[ редактировать ]- Список правильных многогранников
- Выпуклый правильный 4-многогранник
- Тела Кеплера-Пуансо - правильный звездчатый многогранник.
- Звездчатый многоугольник - правильные звездчатые многоугольники.
Ссылки
[ редактировать ]- Эдмунд Гесс , (1883) Введение в теорию сферического деления со специальным рассмотрением ее применения к теории равноповерхностей и равноугольных многогранников [1] .
- HSM Coxeter , Правильные многогранники , 3-е. изд., Dover Publications, 1973. ISBN 0-486-61480-8 .
- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26, Правильные звездчатые многогранники, стр. 404–408)
- Клитцинг, Ричард. «4D однородные многогранники (полихора) x3o3o5/2o - gax» .
Внешние ссылки
[ редактировать ]- Обычная полихора. Архивировано 6 сентября 2003 г. в Wayback Machine.
- Дискуссия об именах
- Правильные многогранники
- Обычная звездная полихора
- Великая 600-ячеечная модель Zome, заархивированная 17 декабря 2022 г. в Wayback Machine [ sic ]
 | Эта из 4-х многогранников статья незавершена . Вы можете помочь Википедии, расширив ее . |