Расположение вершин

В геометрии — расположение вершин это набор точек в пространстве, описываемый их относительным положением. Их можно описать, используя их в многогранниках .

Например, под квадратным расположением вершин понимают четыре точки на плоскости, находящиеся на одинаковом расстоянии и под равными углами от центральной точки.

Два многогранника имеют одинаковое расположение вершин , если они имеют один и тот же 0-скелет .

Группа многогранников, имеющих общее расположение вершин, называется армией .

Расположение вершин

Один и тот же набор вершин может быть соединен ребрами разными способами. Например, пятиугольник и пентаграмма имеют одинаковое расположение вершин , а второй соединяет альтернативные вершины.

Два многоугольника с одинаковым *расположением вершин* .
пятиугольник	пентаграмма

Расположение вершин часто описывается многогранником с выпуклой оболочкой , который его содержит. Например, правильная пентаграмма можно сказать, что имеет (правильное) пятиугольное расположение вершин .

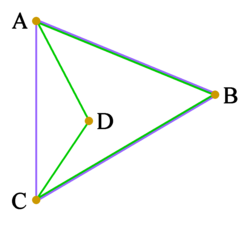	ABCD — вогнутый четырехугольник (зеленый). Его расположение вершин — это множество {A, B, C, D}. Его выпуклая оболочка — треугольник ABC (синий). Расположение вершин выпуклой оболочки - это множество {A, B, C}, которое не совпадает с расположением вершин четырехугольника; Итак, здесь выпуклая оболочка не является способом описания расположения вершин.

Бесконечные мозаики также могут иметь общее расположение вершин .

Например, эту треугольную решетку точек можно соединить, образуя либо равнобедренные треугольники , либо ромбические грани.

Четыре мозаики с одинаковым *расположением вершин* .
Точки решетки	Треугольная плитка	ромбическая плитка	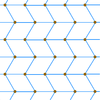Зигзагообразная ромбическая плитка	Ромбическая плитка

Расположение кромок

Многогранники также могут иметь общее расположение ребер , но различаться гранями.

Например, самопересекающийся большой додекаэдр имеет то же расположение ребер, что и выпуклый икосаэдр :

Два многогранника с одинаковым *расположением ребер* .
икосаэдр (20 треугольников)	большой додекаэдр (12 пересекающихся пятиугольников)

Групповые многогранники, которые имеют общее расположение вершин и расположение ребер, называются полками .

Расположение лица

4-многогранники также могут иметь одинаковое расположение граней , что означает, что они имеют одинаковое расположение вершин, ребер и граней, но могут различаться ячейками.

Например, из десяти невыпуклых правильных полихор Шлефли-Гесса имеется только 7 уникальных расположений граней.

Например, большие звездчатые 120-клеточные и большие звездчатые 120-клеточные , оба с пентаграммными гранями, кажутся визуально неотличимыми без изображения их ячеек :

Две (проецируемые) полихоры с одинаковым *расположением граней .*
Большой звездчатый, 120 ячеек (120 маленьких звездчатых додекаэдров )	Большой звездчатый 120-ячеечный (120 больших звездчатых додекаэдров )

Классы подобных многогранников

Джордж Ольшевский защищает термин «полк» для набора многогранников, которые имеют общее расположение ребер, и, в более общем смысле, n-полок для набора многогранников, которые имеют общие элементы до размерности n . Синонимы для особых случаев включают роту для 2-го полка (совместные лица) и армию для 0-полка (совместные вершины).

См. также

n-скелет — совокупность элементов размерности n и ниже в высшем многограннике.
Вершинная фигура — локальное расположение граней в многограннике (или расположение ячеек в многограннике) вокруг одной вершины.

Внешние ссылки

Ольшевский, Георгий. «Армия» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года. (То же расположение вершин)
Ольшевский, Георгий. «Полк» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года. (То же расположение вершин и ребер)
Ольшевский, Георгий. "Компания" . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года. (То же расположение вершин, ребер и граней)