Апейрогональная мозаика порядка 3

Апейрогональная мозаика порядка 3
Модель диска Пуанкаре гиперболической плоскости
Тип	Гиперболическая регулярная мозаика
Конфигурация вершин	∞ ³
Символ Шлефли	{∞,3} т{∞,∞} т(∞,∞,∞)
Символ Витхоффа	3 \| ∞ 2 2 ∞ \| ∞ ∞ ∞ ∞ \|
Диаграмма Кокстера
Группа симметрии	[∞,3], (∞32) [∞,∞], (∞∞2) [(∞,∞,∞)], (*∞∞∞)
Двойной	Треугольная мозаика бесконечного порядка
Характеристики	Вершинно-транзитивный , реберно-транзитивный , грани-транзитивный

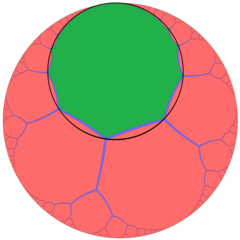
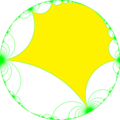
В геометрии апейрогональное замощение порядка 3 — это правильное замощение гиперболической плоскости . Он представлен символом Шлефли {∞,3}, имеющим три правильных апейрогона вокруг каждой вершины. Каждый апейрогон вписан в орицикл .

Апейрогональная мозаика порядка 2 представляет бесконечный диэдр в евклидовой плоскости как {∞,2}.

Изображения

Каждая апейрогона грань описана орициклом , который выглядит как круг в модели диска Пуанкаре , внутренне касающийся границы проективного круга.

Равномерные раскраски

Как и в случае с евклидовой шестиугольной мозаикой , существует три однородные раскраски апейрогональной мозаики порядка 3 , каждая из разных областей группы отражающих треугольников :

Обычный	Усечения
{∞,3}	т _0,1 {∞,∞}	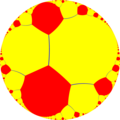т _1,2 {∞,∞}	т{∞ ^[3]}
гиперболических треугольников Группы
[∞,3]	[∞,∞]		[(∞,∞,∞)]

Симметрия

Двойственное этому мозаике представляет фундаментальные области симметрии [(∞,∞,∞)] (*∞∞∞). Существует 15 малых индексных подгрупп (7 уникальных), построенных из [(∞,∞,∞)] путем зеркального удаления и чередования. Зеркала можно удалить, если все его порядки ветвей четные, и это сокращает соседние порядки ветвей пополам. Удаление двух зеркал оставляет точку вращения половинного порядка, где встречаются удаленные зеркала. В этих изображениях фундаментальные области попеременно окрашены в черный и белый цвета, а на границах между цветами существуют зеркала. Симметрию можно удвоить до симметрии ∞∞2 , добавив зеркало, делящее пополам фундаментальную область. Разделение фундаментальной области на 3 зеркала создает симметрию ∞32 .

Строится большая подгруппа [(∞,∞,∞ ^*)], индекс 8, так как (∞*∞ ^∞) с удаленными точками вращения становится (*∞ ^∞).

Подгруппы группы [(∞,∞,∞)] (*∞∞∞)
Index	1	2			4
Diagram
Coxeter	[(∞,∞,∞)]	[(1⁺,∞,∞,∞)] =	[(∞,1⁺,∞,∞)] =	[(∞,∞,1⁺,∞)] =	[(1⁺,∞,1⁺,∞,∞)]	[(∞⁺,∞⁺,∞)]
Orbifold	*∞∞∞	*∞∞∞∞			∞*∞∞∞	∞∞∞×
Diagram
Coxeter		[(∞,∞⁺,∞)]	[(∞,∞,∞⁺)]	[(∞⁺,∞,∞)]	[(∞,1⁺,∞,1⁺,∞)]	[(1⁺,∞,∞,1⁺,∞)] =
Orbifold		∞*∞			∞*∞∞∞
Direct subgroups
Index	2	4			8
Diagram
Coxeter	[(∞,∞,∞)]⁺	[(∞,∞⁺,∞)]⁺ =	[(∞,∞,∞⁺)]⁺ =	[(∞⁺,∞,∞)]⁺ =	[(∞,1⁺,∞,1⁺,∞)]⁺ =
Orbifold	∞∞∞	∞∞∞∞			∞∞∞∞∞∞
Radical subgroups
Index	∞			∞
Diagram
Coxeter	[(∞,∞*,∞)]	[(∞,∞,∞*)]	[(∞*,∞,∞)]	[(∞,∞*,∞)]⁺	[(∞,∞,∞*)]⁺	[(∞*,∞,∞)]⁺
Orbifold	∞*∞^∞			∞^∞

Связанные многогранники и мозаики

Это разбиение топологически связано как часть последовательности правильных многогранников с символом Шлефли {n,3}.

* n 32 мутация симметрии правильных мозаик: { n ,3} v т и
Spherical				Euclidean	Compact hyperb.		Paraco.	Noncompact hyperbolic

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

Паракомпактные равномерные разбиения семейства [∞,3] v т и
Symmetry: [∞,3], (*∞32)							[∞,3]⁺ (∞32)	[1⁺,∞,3] (*∞33)		[∞,3⁺] (3*∞)

		=	=	=				= or	= or	=

{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h₂{∞,3}	s{3,∞}
Uniform duals


V∞³	V3.∞.∞	V(3.∞)²	V6.6.∞	V3^∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞)³		V3.3.3.3.3.∞

Паракомпактные равномерные разбиения семейства [∞,∞] v т и
= =	= =	= =	= =	= =	=	=

{∞,∞}	t{∞,∞}	r{∞,∞}	2t{∞,∞}=t{∞,∞}	2r{∞,∞}={∞,∞}	rr{∞,∞}	tr{∞,∞}
Dual tilings


V∞^∞	V∞.∞.∞	V(∞.∞)²	V∞.∞.∞	V∞^∞	V4.∞.4.∞	V4.4.∞
Alternations
[1⁺,∞,∞] (*∞∞2)	[∞⁺,∞] (∞*∞)	[∞,1⁺,∞] (*∞∞∞∞)	[∞,∞⁺] (∞*∞)	[∞,∞,1⁺] (*∞∞2)	[(∞,∞,2⁺)] (2*∞∞)	[∞,∞]⁺ (2∞∞)


h{∞,∞}	s{∞,∞}	hr{∞,∞}	s{∞,∞}	h₂{∞,∞}	hrr{∞,∞}	sr{∞,∞}
Alternation duals


V(∞.∞)^∞	V(3.∞)³	V(∞.4)⁴	V(3.∞)³	V∞^∞	V(4.∞.4)²	V3.3.∞.3.∞

Паракомпактные равномерные разбиения в семействе [(∞,∞,∞)] v т и



(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) h₂{∞,∞}	(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) h₂{∞,∞}	(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) r{∞,∞}	t(∞,∞,∞) t{∞,∞}
Dual tilings

V∞^∞	V∞.∞.∞.∞	V∞^∞	V∞.∞.∞.∞	V∞^∞	V∞.∞.∞.∞	V∞.∞.∞
Alternations
[(1⁺,∞,∞,∞)] (*∞∞∞∞)	[∞⁺,∞,∞)] (∞*∞)	[∞,1⁺,∞,∞)] (*∞∞∞∞)	[∞,∞⁺,∞)] (∞*∞)	[(∞,∞,∞,1⁺)] (*∞∞∞∞)	[(∞,∞,∞⁺)] (∞*∞)	[∞,∞,∞)]⁺ (∞∞∞)


Alternation duals

V(∞.∞)^∞	V(∞.4)⁴	V(∞.∞)^∞	V(∞.4)⁴	V(∞.∞)^∞	V(∞.4)⁴	V3.∞.3.∞.3.∞

См. также

Замощения правильных многоугольников
Список однородных плоских мозаик
Список правильных многогранников
Шестиугольные соты для плитки , аналогичные соты {6,3,3} в H ³.

Ссылки

Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
«Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .

Внешние ссылки