Регулярная сетка

Пример обычной сетки

Регулярная сетка — это мозаика конгруэнтными n -мерного евклидова пространства параллелоэдрами кирпичами ( например, ) . Его противоположностью является нерегулярная сетка .

Сетки этого типа появляются на миллиметровой бумаге и могут использоваться в анализе методом конечных элементов , методах конечных объемов , методах конечных разностей и в целом для дискретизации пространств параметров. Поскольку производные полевых переменных удобно выражать как конечные разности, структурированные сетки в основном появляются в методах конечных разностей. Неструктурированные сетки обеспечивают большую гибкость, чем структурированные сетки, и, следовательно, очень полезны в методах конечных элементов и конечных объемов.

К каждой ячейке сетки можно обращаться по индексу (i, j) в двух измерениях или (i, j, k) в трех измерениях, и каждая вершина имеет координаты. $(i\cdot dx,j\cdot dy)$ в 2D или $(i\cdot dx,j\cdot dy,k\cdot dz)$ в 3D для некоторых действительных чисел dx , dy и dz, представляющих шаг сетки.

Связанные сетки

Декартова сетка — это особый случай, когда элементами являются единичные квадраты или единичные кубы , а вершины — точки целочисленной решетки .

представляет Прямолинейная сетка собой мозаику из прямоугольников или прямоугольных кубоидов (также известных как прямоугольные параллелепипеды ), которые, как правило, не все конгруэнтны друг другу. Ячейки по-прежнему могут индексироваться целыми числами, как указано выше, но сопоставление индексов с координатами вершин менее единообразно, чем в обычной сетке. Пример прямолинейной сетки, которая не является регулярной, показан на логарифмического масштаба миллиметровой бумаге .

представляет Перекошенная сетка собой мозаику из параллелограммов или параллелепипедов . (Если все единицы длины равны, это мозаика из ромбов или ромбоэдров .)

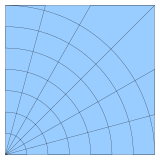
Криволинейная сетка или структурированная сетка — это сетка с той же комбинаторной структурой, что и обычная сетка, в которой ячейки представляют собой четырехугольники или [общие] кубоиды , а не прямоугольники или прямоугольные кубоиды.

Примеры различных сеток

• 
  3-D декартова сетка
• 
  3-D прямолинейная сетка
• 
  2D криволинейная сетка
• 
  Некриволинейная комбинация различных двумерных криволинейных сеток
• 
  2D треугольная сетка.

См. также

• Декартова система координат - наиболее распространенная система координат (геометрия).
• Целочисленная решетка - группа решетки в евклидовом пространстве, точки которой представляют собой целые n-кортежи.
• Неструктурированная сетка . Неструктурированная (или нерегулярная) сетка представляет собой мозаику части евклидовой плоскости.
• Дискретизация - процесс перевода непрерывных функций в дискретные аналоги.