Конструкция Гольдберга – Кокстера

Многогранник Гольдберга (3,1) и геодезический многогранник (3,1). Многогранники Гольдберга и геодезические многогранники были предшественниками операции Гольдберга – Коксетера.

Конструкция Гольдберга -Коксетера или операция Голдберга-Коксетера ( конструкция GC или операция GC ) — это операция над графом, определенная на правильных многогранных графах степени 3 или 4. ^[1]^[2] Это также относится к двойственному графу этих графов, то есть графам с треугольными или четырехугольными «гранями». Конструкцию GC можно рассматривать как подразделение граней многогранника решеткой из треугольных, квадратных или шестиугольных многоугольников, возможно, перекошенных по отношению к исходной грани: это расширение концепций, введенных многогранниками Гольдберга и геодезическими многогранниками . Конструкция GC в первую очередь изучается в органической химии на предмет ее применения к фуллеренам . ^[1]^[2] но это было применено к наночастицам , ^[3] компьютерное проектирование , ^[4] плетение корзин , ^[5]^[6] и общее изучение теории графов и многогранников . ^[7]

Конструкция Гольдберга–Коксетера может быть обозначена как $GC_{k,\ell }(G_{0})$ , где $G_{0}$ над которым ведется работа, $k$ и $l$ являются целыми числами, $k>0$ , и $\ell \geq 0$ .

История

Майкл Голдберг представил многогранник Гольдберга в 1937 году. ^[8] Бакминстер Фуллер ввел термин « геодезический купол » в 1940-х годах, хотя в значительной степени держал математические расчеты, лежащие в основе куполов, в коммерческой тайне. ^[9] Геодезические купола — это геометрический двойник (часть) многогранника Гольдберга: полный геодезический купол можно рассматривать как геодезический многогранник , двойственный многограннику Гольдберга. В 1962 году Дональд Каспар и Аарон Клуг опубликовали статью о геометрии вирусных капсидов , в которой были применены и расширены концепции Голдберга и Фуллера. ^[10] HSM Coxeter опубликовал в 1971 году статью, в которой содержалась большая часть той же информации. ^[11] Каспар и Клуг были первыми, кто опубликовал наиболее общую правильную конструкцию геодезического многогранника, сделав название «конструкция Гольдберга-Коксетера» примером закона эпонимии Стиглера . ^[12]

Открытие бакминстерфуллерена в 1985 году стимулировало исследования других молекул со структурой многогранника Гольдберга. Термины «фуллерен Гольдберга – Кокстера» и «конструкция Гольдберга – Кокстера» были введены Мишелем Деза в 2000 году. ^[13]^[14] Также впервые рассматривается случай 4-й степени.

Строительство

Этот раздел во многом следует двум статьям Деза и др.. ^[1]^[2]

Мастер-полигоны

Решетки
n-Обычный	3	4
Домен	Эйзенштейн $a+bu$	Гауссовский $a+bi$
Примыкающий единица	${\begin{aligned}u&={\frac {1}{2}}\left(1+i{\sqrt {3}}\right)\\&=e^{{\frac {1}{3}}\pi i}=\omega +1\end{aligned}}$	$i={\sqrt {-1}}$
Норма $t(a,b)$	$a^{2}+ab+b^{2}$	$a^{2}+b^{2}$ .
Мастер-полигон	$(0,x,xu)$	$(0,x,x(1+i),xi)$

Регулярные решетки на комплексной плоскости можно использовать для создания «главных многоугольников». В терминологии геодезических куполов это «структура разрушения» или «главный многогранный треугольник» (ППТ). В 4-регулярном случае используется квадратная решетка над целыми числами Гаусса , а в 3-регулярном случае используется треугольная решетка над целыми числами Эйзенштейна . Для удобства используется альтернативная параметризация целых чисел Эйзенштейна, основанная на корне шестой степени из единицы вместо третьего. ^[а] Обычное определение целых чисел Эйзенштейна использует элемент ${\textstyle \omega ={\frac {1}{2}}\left(-1+i{\sqrt {3}}\right)=e^{{\frac {2}{3}}\pi i}=u-1}$ . Норма, $t(k,\ell )$ , определяется как квадрат абсолютного значения комплексного числа . Для 3-регулярных графов этой нормой является Т-число или число триангуляции, используемое в вирусологии.

Главный многоугольник представляет собой равносторонний треугольник или квадрат, наложенный на решетку. В таблице справа приведены формулы для вершин главных многоугольников на комплексной плоскости, а в галерее ниже показаны основные треугольник и квадрат (3,2). Чтобы многоугольник можно было описать одним комплексным числом, одна вершина фиксируется в 0. Существует несколько чисел, которые могут описывать один и тот же многоугольник: это ассоциированные числа друг друга: если $x$ и $y$ являются соратниками, то $x=u^{n}y$ у Эйзенштейнов или $x=i^{n}y$ в гауссианах для некоторого целого числа $n$ . Множество элементов, которые являются ассоциированными друг с другом, представляет собой класс эквивалентности , и элемент каждого класса эквивалентности, имеющий $a>0$ и $b\geq 0$ это нормальная форма .

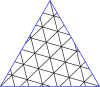
(3,2) главный треугольник над треугольной сеткой
(3,2) основной квадрат над квадратной сеткой

Мастер-полигоны и оператор $GC_{k,\ell }\left(G_{0}\right)$ , можно классифицировать следующим образом:

Класс I: $\ell =0.$
Класс II: $k=\ell .$
Класс III: все прочее. Операторы класса III существуют в киральных парах: $GC_{k,\ell }\left(G_{0}\right)$ представляет собой киральную пару $GC_{\ell ,k}(G_{0})$ .

Ниже приведены таблицы основных треугольников и квадратов. Класс I соответствует первому столбцу, а класс II соответствует диагонали с немного более темным фоном.

Мастер-полигоны для треугольников

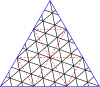
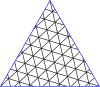
Мастер-треугольники через (8,8)
	0	1	2	3	4	5	6	7	8
1
2
3
4
5
6
7
8

Мастер-полигоны для квадратов

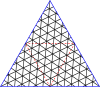
Мастер-квадраты через (8,8)
	0	1	2	3	4	5	6	7	8
1
2
3
4
5
6
7
8

Композиция операций Гольдберга – Кокстера соответствует умножению комплексных чисел. Если и только если $GC_{a,b}\left(GC_{c,d}\left(G_{0}\right)\right)=GC_{e,f}\left(G_{0}\right)$ (т.е. серия операций слева дает граф, изоморфный правому), то для 3-регулярного графа $(a+bu)(c+du)$ находится в классе эквивалентности $(e+fu)$ , а для 4-регулярного графа $(a+bi)(c+di)$ находится в классе эквивалентности $(e+fi)$ . Из этого есть несколько полезных последствий:

Применение повторяющихся операций Гольдберга – Кокстера коммутативно и ассоциативно .
Комплексное сопряжение элемента $a+bi$ или $a+bu$ соответствует отражению построенного графа.
Поскольку целые числа Гаусса и целые евклидовы числа являются евклидовыми областями , элементы этих областей могут быть однозначно разложены на простые элементы. Поэтому имеет смысл также разложить оператор Гольдберга–Коксетера на последовательность «простых» операторов Гольдберга–Кокстера, причем эта последовательность уникальна (с точностью до перестановки).

Выполнение строительства ГК

Этапы выполнения строительства ГК $GC_{k,\ell }(G_{0})$ следующие:

Определите главный полигон на основе $k$ , $\ell$ , и $G_{0}$
Если вы оперируете 3- или 4-регулярным графом (вместо графа с треугольными/четырехугольными гранями), возьмите его двойственный граф . Этот двойственный граф будет иметь треугольные или четырехугольные грани.
Замените грани триангулированного/четырёхугольного графа основным многоугольником. Имейте в виду, что плоские графы имеют «внешнюю» грань, которую также необходимо заменить. В приведенном ниже примере это делается путем прикрепления его к одной стороне графика и соединения других сторон по мере необходимости. Это временно вводит в граф перекрывающиеся ребра, но в результате граф оказывается плоским. Вершины можно переставлять так, чтобы не было перекрывающихся ребер.
Если исходный граф был 3- или 4-регулярным, возьмите двойственный результат шага 3. В противном случае результатом шага 3 является конструкция GC.

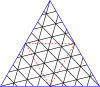
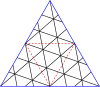
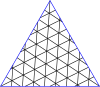
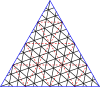
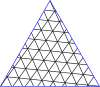
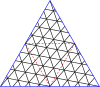
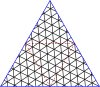
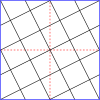
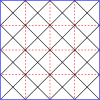
Ниже приведен пример, где $GC_{1,1}(G_{0})$ построен скелете куба . на На последних двух графиках синие линии — это ребра $G_{0}$ , а черные линии — это края $GC_{1,1}(G_{0})$ . (Пунктирные линии — это обычные ребра графа, просто нарисованные по-другому, чтобы сделать перекрывающиеся ребра графа более заметными.) Красные вершины находятся внутри. $G_{0}$ и оставаться в $GC_{1,1}(G_{0})$ , а синие вершины создаются конструкцией заново и находятся только в $GC_{1,1}(G_{0})$ .

Мастер-сквер (1,1)
Начальный многогранник (Куб)
$G_{0}$ , скелет куба
Промежуточный этап строительства $GC_{1,1}(G_{0})$ .
Результат $GC_{1,1}(G_{0})$ , после перестановки
Вложение результата ( ромбдодекаэдр )

Расширения

Конструкция Гольдберга-Коксетера может быть легко распространена на некоторые неплоские графы, такие как тороидальные графы . ^[15] Операторы класса III из-за своей киральности требуют графа, который можно встроить на ориентируемую поверхность , но операторы классов I и II можно использовать на неориентируемых графах.

См. также

Сноски

^ Это упрощает определение класса эквивалентности, делает определение класса одинаковым для 3- и 4-регулярных графов и соответствует параметризации, традиционно используемой для геодезических куполов и многогранников Гольдберга.

Ссылки

^ Перейти обратно: ^а ^б ^с Деза, М.; Дютур, М (2004). «Конструкции Гольдберга – Кокстера для 3- и 4-валентных плоских графов» . Электронный журнал комбинаторики . 11 : #R20. дои : 10.37236/1773 .
^ Перейти обратно: ^а ^б ^с Деза, М.-М.; Сикирич, доктор медицинских наук; Штогрин, М.И. (2015). «Построение и параметризация Гольдберга – Кокстера» . Геометрическая структура графиков, имеющих отношение к химии: зигзаги и центральные цепи . Спрингер. стр. 131–148. ISBN 9788132224495 .
^ Инделикато, Г; Буркхард, П; Тварок, Р. (2017). «Классификация архитектур самособирающихся белковых наночастиц для применения в разработке вакцин» . Королевское общество открытой науки . 4 (4): 161092. Бибкод : 2017RSOS....461092I . дои : 10.1098/rsos.161092 . ПМЦ 5414263 . ПМИД 28484626 .
^ Котани, М; Найто, Х; Омори, Т (2017). «Теория дискретной поверхности» . Компьютерное геометрическое проектирование . 58 : 24–54. дои : 10.1016/j.cagd.2017.09.002 .
^ Тарнаи, Т. (2006). Корзины (PDF) . IASS-APCS 2006 Межд. Симп. Новая Олимпиада. Новые оболочки и пространственные структуры. Пекинский технологический университет: международный доц. для оболочечных и пространственных конструкций. стр. ИЛ09.
^ Тарнаи, Т.; Ковач, Ф.; Фаулер, П.В.; Гость, СД (2012). «Обвертывание куба и других многогранников» . Труды Королевского общества А. 468 (2145): 2652. Бибкод : 2012RSPSA.468.2652T . дои : 10.1098/rspa.2012.0116 .
^ Никодимос, Диего; Стелик, Матей (2018). «Упаковка и покрытие нечетных циклов в графах кубической плоскости с маленькими гранями». Европейский журнал комбинаторики . 67 : 208–221. arXiv : 1701.07748 . дои : 10.1016/j.ejc.2017.08.004 . S2CID 27137740 .
^ Гольдберг, М. (1937). «Класс мультисимметричных многогранников». Математический журнал Тохоку .
^ Кеннер, Х. (1976). Геодезическая математика и как ее использовать . Издательство Калифорнийского университета.
^ Каспар, DLD; Клюг, А. (1962). «Физические принципы построения обычных вирусов». Холодный источник Харб. Симп. Квант. Биол . 27 : 1–24. дои : 10.1101/sqb.1962.027.001.005 . ПМИД 14019094 .
^ Коксетер, HSM (1971). «Вирусные макромолекулы и геодезические купола». В Батчере, Джей Си (ред.). Спектр математики . Издательство Оксфордского университета. стр. 98–107.
^ Бринкманн, Г.; Гетшалькс, П.; Шейн, С. (2017). «Гольдберг, Фуллер, Каспар, Клюг и Коксетер и общий подход к операциям, сохраняющим локальную симметрию». Труды Королевского общества А. 473 (2206): 20170267.arXiv : 1705.02848 . Бибкод : 2017RSPSA.47370267B . дои : 10.1098/rspa.2017.0267 . S2CID 119171258 .
^ Деза, М; Фаулер, П.В.; Рассат, А; Роджерс, К.М. (2000). «Фуллерены как мозаика поверхностей». Журнал химической информации и компьютерных наук . 40 (3): 550–8. CiteSeerX 10.1.1.105.5973 . дои : 10.1021/ci990066h . ПМИД 10850758 .
^ Хирш, Андреас; Чен, Чжунфан; Цзяо, Хайцзюнь (2000). «Сферическая ароматичность в симметричных фуллеренах: правило 2 (N + 1) 2». Ангеванде Хеми . 39 (21): 3915–3917. doi : 10.1002/1521-3773(20001103)39:21<3915::AID-ANIE3915>3.0.CO;2-O . ПМИД 29711706 .
^ Деза, Мишель-Мари; Сикирич, Матье Дютур (2016). «Легоподобные сферы и торы». Журнал математической химии . 55 (3): 752. doi : 10.1007/s10910-016-0706-8 . S2CID 125087322 .

[15] Это упрощает определение класса эквивалентности, делает определение класса одинаковым для 3- и 4-регулярных графов и соответствует параметризации, традиционно используемой для геодезических куполов и многогранников Гольдберга.

[Deza2004-1] Перейти обратно: ^а ^б ^с Деза, М.; Дютур, М (2004). «Конструкции Гольдберга – Кокстера для 3- и 4-валентных плоских графов» . Электронный журнал комбинаторики . 11 : #R20. дои : 10.37236/1773 .

[Deza2015-2] Перейти обратно: ^а ^б ^с Деза, М.-М.; Сикирич, доктор медицинских наук; Штогрин, М.И. (2015). «Построение и параметризация Гольдберга – Кокстера» . Геометрическая структура графиков, имеющих отношение к химии: зигзаги и центральные цепи . Спрингер. стр. 131–148. ISBN 9788132224495 .

[3] Инделикато, Г; Буркхард, П; Тварок, Р. (2017). «Классификация архитектур самособирающихся белковых наночастиц для применения в разработке вакцин» . Королевское общество открытой науки . 4 (4): 161092. Бибкод : 2017RSOS....461092I . дои : 10.1098/rsos.161092 . ПМЦ 5414263 . ПМИД 28484626 .

[4] Котани, М; Найто, Х; Омори, Т (2017). «Теория дискретной поверхности» . Компьютерное геометрическое проектирование . 58 : 24–54. дои : 10.1016/j.cagd.2017.09.002 .

[5] Тарнаи, Т. (2006). Корзины (PDF) . IASS-APCS 2006 Межд. Симп. Новая Олимпиада. Новые оболочки и пространственные структуры. Пекинский технологический университет: международный доц. для оболочечных и пространственных конструкций. стр. ИЛ09.

[6] Тарнаи, Т.; Ковач, Ф.; Фаулер, П.В.; Гость, СД (2012). «Обвертывание куба и других многогранников» . Труды Королевского общества А. 468 (2145): 2652. Бибкод : 2012RSPSA.468.2652T . дои : 10.1098/rspa.2012.0116 .

[7] Никодимос, Диего; Стелик, Матей (2018). «Упаковка и покрытие нечетных циклов в графах кубической плоскости с маленькими гранями». Европейский журнал комбинаторики . 67 : 208–221. arXiv : 1701.07748 . дои : 10.1016/j.ejc.2017.08.004 . S2CID 27137740 .

[8] Гольдберг, М. (1937). «Класс мультисимметричных многогранников». Математический журнал Тохоку .

[9] Кеннер, Х. (1976). Геодезическая математика и как ее использовать . Издательство Калифорнийского университета.

[10] Каспар, DLD; Клюг, А. (1962). «Физические принципы построения обычных вирусов». Холодный источник Харб. Симп. Квант. Биол . 27 : 1–24. дои : 10.1101/sqb.1962.027.001.005 . ПМИД 14019094 .

[11] Коксетер, HSM (1971). «Вирусные макромолекулы и геодезические купола». В Батчере, Джей Си (ред.). Спектр математики . Издательство Оксфордского университета. стр. 98–107.

[Brinkmann-12] Бринкманн, Г.; Гетшалькс, П.; Шейн, С. (2017). «Гольдберг, Фуллер, Каспар, Клюг и Коксетер и общий подход к операциям, сохраняющим локальную симметрию». Труды Королевского общества А. 473 (2206): 20170267.arXiv : 1705.02848 . Бибкод : 2017RSPSA.47370267B . дои : 10.1098/rspa.2017.0267 . S2CID 119171258 .

[13] Деза, М; Фаулер, П.В.; Рассат, А; Роджерс, К.М. (2000). «Фуллерены как мозаика поверхностей». Журнал химической информации и компьютерных наук . 40 (3): 550–8. CiteSeerX 10.1.1.105.5973 . дои : 10.1021/ci990066h . ПМИД 10850758 .

[14] Хирш, Андреас; Чен, Чжунфан; Цзяо, Хайцзюнь (2000). «Сферическая ароматичность в симметричных фуллеренах: правило 2 (N + 1) 2». Ангеванде Хеми . 39 (21): 3915–3917. doi : 10.1002/1521-3773(20001103)39:21<3915::AID-ANIE3915>3.0.CO;2-O . ПМИД 29711706 .

[16] Деза, Мишель-Мари; Сикирич, Матье Дютур (2016). «Легоподобные сферы и торы». Журнал математической химии . 55 (3): 752. doi : 10.1007/s10910-016-0706-8 . S2CID 125087322 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[а]

[15]