Каноническая форма

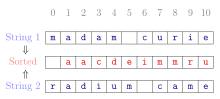
В математике и информатике каноническая , — нормальная или стандартная форма математического объекта это стандартный способ представления этого объекта в виде математического выражения . Часто это тот, который обеспечивает простейшее представление объекта и позволяет его идентифицировать уникальным способом. Различие между «каноническими» и «нормальными» формами варьируется от подполя к подполю. В большинстве полей каноническая форма определяет уникальное представление для каждого объекта, тогда как нормальная форма просто определяет его форму без требования уникальности. ^[1]

Каноническая форма натурального числа в десятичном представлении — это конечная последовательность цифр, не начинающаяся с нуля. В более общем смысле, для класса объектов, на которых определено отношение эквивалентности , каноническая форма состоит в выборе конкретного объекта в каждом классе. Например:

Жорданова нормальная форма является канонической формой подобия матриц .
Форма эшелона строк является канонической формой, когда считается эквивалентной матрица и ее левое произведение на обратимую матрицу .

В информатике, а точнее в компьютерной алгебре , при представлении математических объектов в компьютере обычно существует множество разных способов представления одного и того же объекта. В этом контексте каноническая форма — это такое представление, при котором каждый объект имеет уникальное представление (при этом канонизация — это процесс, посредством которого представление приводится в его каноническую форму). ^[2] Таким образом, равенство двух объектов можно легко проверить, проверив равенство их канонических форм.

Несмотря на это преимущество, канонические формы часто зависят от произвольного выбора (например, упорядочения переменных), что создает трудности при проверке равенства двух объектов, возникающих в результате независимых вычислений. Следовательно, в компьютерной алгебре нормальная форма — более слабое понятие: нормальная форма — это представление, в котором ноль представлен однозначно. Это позволяет проверять равенство, придавая разнице двух объектов нормальную форму.

Каноническая форма также может означать дифференциальную форму , определенную естественным (каноническим) способом.

Определение

Учитывая набор S объектов с отношением эквивалентности R на S , каноническая форма задается путем обозначения некоторых объектов S как находящихся «в канонической форме», так что каждый рассматриваемый объект эквивалентен ровно одному объекту в канонической форме. Другими словами, канонические формы в S представляют классы эквивалентности один и только один раз. Чтобы проверить, эквивалентны ли два объекта, достаточно проверить равенство их канонических форм.Таким образом, каноническая форма обеспечивает классификационную теорему и многое другое, поскольку она не только классифицирует каждый класс, но также дает выдающегося (канонического) представителя для каждого объекта в классе.

Формально канонизация по отношению эквивалентности R на множестве S это отображение c : S → S что для всех s , s1 _— , s2 _{такое ,} ∈ S :

c ( s ) = c ( c ( s )) ( идемпотентность ),
s ₁ R s ₂ тогда и только тогда, когда c ( s ₁ ) = c ( s ₂ ) (решительность), и
s R c ( s ) (репрезентативность).

Свойство 3 является избыточным; это следует путем применения 2 к 1.

С практической точки зрения часто бывает полезно распознавать канонические формы. Также необходимо рассмотреть практический, алгоритмический вопрос: как перейти от данного объекта s из S к его канонической форме s *? Канонические формы обычно используются для повышения эффективности работы с классами эквивалентности. Например, в модульной арифметике канонической формой класса вычетов обычно считается наименьшее неотрицательное целое число в нем. Операции над классами осуществляются путем объединения этих представителей и последующего приведения результата к наименьшему неотрицательному остатку.Требование уникальности иногда ослабляется, позволяя формам быть уникальными с точностью до некоторого более тонкого отношения эквивалентности, например, допуская изменение порядка терминов (если нет естественного порядка терминов).

Каноническая форма может быть просто соглашением или глубокой теоремой. Например, многочлены принято записывать слагаемыми в убывающих степенях: чаще пишут x ² + х + 30, чем х + 30 + х ², хотя обе формы определяют один и тот же полином. Напротив, существование жордановой канонической формы матрицы является глубокой теоремой.

История

Согласно OED и LSJ , термин канонический происходит от древнегреческого слова kanonikós ( κανονικός , «регулярный, согласно правилу») от kanṓn ( κᾰνών , «жезл, правило»). Чувство нормы , стандарта или архетипа использовалось во многих дисциплинах. Математическое использование засвидетельствовано в письме Логана от 1738 года . ^[3] Немецкий термин «kanonische Form» засвидетельствован в статье Эйзенштейна 1846 года : ^[4] позже в том же году Ришело использует термин нормальная форма в статье: ^[5] а в 1851 году Сильвестр пишет: ^[6]

«Теперь я перехожу к [...] способу сведения алгебраических функций к их простейшим и наиболее симметричным, или, как мой замечательный друг М. Эрмит вполне предлагает назвать их, к их каноническим формам ».

В тот же период использование засвидетельствовано Гессе («Нормальная форма»), ^[7] Отшельник («каноническая форма»), ^[8] Борхардт («каноническая форма»), ^[9] и Кэли («каноническая форма»). ^[10]

В 1865 году Словарь науки, литературы и искусства определяет каноническую форму как:

«В математике обозначает форму, обычно самую простую или наиболее симметричную, к которой без потери общности можно свести все функции одного класса».

Примеры

Примечание: в этом разделе « до » некоторого отношения эквивалентности E означает, что каноническая форма вообще не уникальна, но что если один объект имеет две разные канонические формы, они E-эквивалентны.

Обозначение больших чисел

Стандартная форма используется многими математиками и учеными для записи чрезвычайно больших чисел более кратким и понятным способом, наиболее известной из которых является научная запись . ^[11]

Теория чисел

Каноническое представление натурального числа
Каноническая форма цепной дроби

Линейная алгебра

Объекты	A эквивалентно B, если:	Нормальная форма	Примечания
Нормальные матрицы над комплексными числами	$A=U^{*}BU$ для некоторой унитарной матрицы U	Диагональные матрицы (с точностью до переупорядочения)	Это спектральная теорема
Матрицы над комплексными числами	$A=UBV^{*}$ для некоторых унитарных матриц U и V	Диагональные матрицы с действительными положительными элементами (в порядке убывания)	Разложение по сингулярным значениям
Матрицы над алгебраически замкнутым полем	$A=P^{-1}BP$ для некоторой обратимой матрицы P	Жорданова нормальная форма (с точностью до переупорядочения блоков)
Матрицы над алгебраически замкнутым полем	$A=P^{-1}BP$ для некоторой обратимой матрицы P	Каноническая форма Вейра (вплоть до переупорядочения блоков)
Матрицы над полем	$A=P^{-1}BP$ для некоторой обратимой матрицы P	Нормальная форма Фробениуса
Матрицы над областью главных идеалов	$A=P^{-1}BQ$ для некоторых обратимых матриц P и Q	Смит, нормальная форма	Эквивалентность аналогична разрешению обратимых элементарных преобразований строк и столбцов.
Матрицы над целыми числами	$A=UB$ для некоторой унимодулярной матрицы U	Эрмитская нормальная форма
Матрицы целых чисел по модулю n		Хауэлл нормальная форма
Конечномерные векторные пространства над полем K	A и B изоморфны как векторные пространства.	$K^{n}$ , n неотрицательное целое число

Алгебра

Объекты	A эквивалентно B, если:	Нормальная форма
Конечно порожденные R -модули с R областью главного идеала	A и B изоморфны как R -модули	Первичная декомпозиция (вплоть до переупорядочения) или инвариантная факторная декомпозиция

Геометрия

В аналитической геометрии :

Уравнение линии: Ax + By = C , где A ² + Б ² = 1 и C ≥ 0
Уравнение окружности: $(x-h)^{2}+(y-k)^{2}=r^{2}$

Напротив, существуют альтернативные формы записи уравнений. Например, уравнение линии может быть записано как линейное уравнение в форме наклона точки и точки пересечения наклона .

Выпуклым многогранникам можно привести каноническую форму так, что:

Все лица плоские,
Все ребра касаются единичной сферы, а
Центр тяжести многогранника находится в начале координат. ^[12]

Интегрируемые системы

Каждое дифференцируемое многообразие имеет кокасательное расслоение . Этому расслоению всегда можно наделить некоторую дифференциальную форму , называемую канонической одноформой . Эта форма придает кокасательному расслоению структуру симплектического многообразия и позволяет интегрировать векторные поля на многообразии с помощью уравнений Эйлера-Лагранжа или с помощью гамильтоновой механики . Такие системы интегрируемых дифференциальных уравнений называются интегрируемыми системами .

Динамические системы

Изучение динамических систем частично совпадает с изучением интегрируемых систем ; там есть идея нормальной формы (динамических систем) .

Трехмерная геометрия

При изучении трехмерных многообразий есть первая фундаментальная форма , вторая фундаментальная форма и третья фундаментальная форма .

Функциональный анализ

Объекты	A эквивалентно B, если:	Нормальная форма
гильбертовы пространства	Если A и B являются гильбертовыми пространствами бесконечной размерности, то A и B изометрически изоморфны.	$\ell ^{2}(I)$ пространства последовательностей (вплоть до замены набора индексов I на другой набор индексов той же мощности )
Коммутативные C*-алгебры с единицей	A и B изоморфны как C*-алгебры	Алгебра $C(X)$ непрерывных функций на компакте хаусдорфовом с точностью до гомеоморфизма базисного пространства.

Системы перезаписи

Символическое преобразование формулы из одной формы в другую называется «переписыванием» этой формулы. Можно изучить абстрактные свойства переписывания общих формул, изучая набор правил, с помощью которых формулами можно правильно манипулировать. Это «правила переписывания» — неотъемлемая часть абстрактной системы переписывания . Общий вопрос заключается в том, можно ли привести некоторое родовое выражение к единой, общей форме, нормальной форме. Если различные последовательности перезаписей по-прежнему приводят к одной и той же форме, то эту форму можно назвать нормальной формой, а перезапись - сливающейся. Не всегда удается получить нормальную форму.

Лямбда-исчисление

Лямбда-член находится в бета-нормальной форме, если бета-редукция невозможна; Лямбда-исчисление — это частный случай абстрактной системы переписывания. Например, в нетипизированном лямбда-исчислении термин $(\lambda x.(xx)\;\lambda x.(xx))$ не имеет нормальной формы. В типизированном лямбда-исчислении каждый правильно сформированный термин можно переписать в его нормальную форму.

Теория графов

В теории графов , разделе математики, канонизация графов — это проблема нахождения канонической формы данного G. графа Каноническая форма — это помеченный граф Canon( G ), изоморфный G , такой, что каждый граф, изоморфный G имеет ту же каноническую форму, что и G. , Таким образом, из решения проблемы канонизации графов можно также решить проблему изоморфизма графов : проверить, ли два графа G и H изоморфны , вычислить их канонические формы Canon( G ) и Canon( H ) и проверить, являются ли эти графы изоморфными. две канонические формы идентичны.

Вычисление

В вычислительной технике приведение данных к любой канонической форме обычно называется нормализацией данных .

Например, нормализация базы данных — это процесс организации полей и таблиц реляционной базы данных для минимизации избыточности и зависимостей. ^[13]

В области безопасности программного обеспечения распространенной уязвимостью является непроверенный вредоносный ввод (см. Внедрение кода ). Решением этой проблемы является правильная проверка ввода . Прежде чем будет выполнена проверка входных данных, входные данные обычно нормализуются путем устранения кодирования (например, кодирования HTML ) и сведения входных данных к одному общему набору символов .

Другие формы данных, обычно связанные с обработкой сигналов (включая аудио и изображения ) или машинным обучением , могут быть нормализованы, чтобы обеспечить ограниченный диапазон значений.

В управлении контентом концепция единого источника истины применима (SSOT), так же, как и в нормализации баз данных в целом и в разработке программного обеспечения . Грамотные системы управления контентом предоставляют логические способы его получения, например включение .

См. также

Примечания

^ В некоторых случаях термины «канонический» и «нормальный» также могут использоваться как взаимозаменяемые, например, в канонической форме Джордана и нормальной форме Джордана (см. Нормальную форму Джордана в MathWorks ).
↑ Для этого иногда неправильно используют термин «канонизация».
^ Письмо Джеймса Логана Уильяму Джонсу, Переписка ученых семнадцатого века . Университетское издательство. 1841. ISBN 978-1-02-008678-6 .
^ «Журнал чистой и прикладной математики 1846 г.» . де Грюйтер.
^ Журнал чистой и прикладной математики 1846 года . де Грюйтер.
^ «Математический журнал Кембриджа и Дублина, 1851 год» . Макмиллан.
^ Гессен, Отто (1865). «Лекции по аналитической геометрии прямой, точки и окружности на плоскости» (на немецком языке). Тойбнер.
^ «Математический журнал Кембриджа и Дублина, 1854 год» . 1854.
^ «Журнал чистой и прикладной математики, 1854 год» . де Грюйтер.
^ Кэли, Артур (1889). Сборник математических статей . Университет. ISBN 978-1-4181-8586-2 .
^ «Большие числа и научная запись» . Обучение количественной грамотности . Проверено 20 ноября 2019 г.
^ Циглер, Гюнтер М. (1995), Лекции по многогранникам , Тексты для аспирантов по математике, том. 152, Springer-Verlag, стр. 117–118, ISBN. 0-387-94365-Х
^ «Описание основ нормализации баз данных» . support.microsoft.com . Проверено 20 ноября 2019 г.

Ссылки

Shilov, Georgi E. (1977), Silverman, Richard A. (ed.), Linear Algebra , Dover, ISBN 0-486-63518-Х .
Хансен, Вагн Лундсгаард (2006), Функциональный анализ: вход в гильбертово пространство , World Scientific Publishing, ISBN 981-256-563-9 .

[1] В некоторых случаях термины «канонический» и «нормальный» также могут использоваться как взаимозаменяемые, например, в канонической форме Джордана и нормальной форме Джордана (см. Нормальную форму Джордана в MathWorks ).

[2] Для этого иногда неправильно используют термин «канонизация».

[3] Письмо Джеймса Логана Уильяму Джонсу, Переписка ученых семнадцатого века . Университетское издательство. 1841. ISBN 978-1-02-008678-6 .

[4] «Журнал чистой и прикладной математики 1846 г.» . де Грюйтер.

[5] Журнал чистой и прикладной математики 1846 года . де Грюйтер.

[6] «Математический журнал Кембриджа и Дублина, 1851 год» . Макмиллан.

[7] Гессен, Отто (1865). «Лекции по аналитической геометрии прямой, точки и окружности на плоскости» (на немецком языке). Тойбнер.

[8] «Математический журнал Кембриджа и Дублина, 1854 год» . 1854.

[9] «Журнал чистой и прикладной математики, 1854 год» . де Грюйтер.

[10] Кэли, Артур (1889). Сборник математических статей . Университет. ISBN 978-1-4181-8586-2 .

[11] «Большие числа и научная запись» . Обучение количественной грамотности . Проверено 20 ноября 2019 г.

[12] Циглер, Гюнтер М. (1995), Лекции по многогранникам , Тексты для аспирантов по математике, том. 152, Springer-Verlag, стр. 117–118, ISBN. 0-387-94365-Х

[13] «Описание основ нормализации баз данных» . support.microsoft.com . Проверено 20 ноября 2019 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]