Каноническая форма Вейра

На изображении показан пример общей матрицы Вейра, состоящей из двух блоков, каждый из которых является базовой матрицей Вейра. Основная матрица Вейра в верхнем левом углу имеет структуру (4,2,1), а другая — структуру (2,2,1,1).

В математике , в линейной алгебре , каноническая форма Вейра (или форма Вейра или матрица Вейра ) представляет собой квадратную матрицу , которая (в некотором смысле) индуцирует «хорошие» свойства матриц, с которыми она коммутирует. Он также имеет особенно простую структуру, а условия существования формы Вейра довольно слабы, что делает его подходящим инструментом для изучения классов коммутирующих матриц. Говорят, что квадратная матрица находится в Вейра канонической форме , если матрица имеет структуру, определяющую каноническую форму Вейра. Форма Вейра была открыта чешским математиком Эдуардом Вейром в 1885 году. Форма Вейра не стала популярной среди математиков, и ее затмила близкородственная, но отличная каноническая форма, известная под названием каноническая форма Иордана . Форма Вейра несколько раз открывалась заново с момента первоначального открытия Вейра в 1885 году. Эту форму по-разному называли модифицированной жордановой формой, переупорядоченной жордановой формой, второй жордановой формой и H-формой . Текущая терминология принадлежит Шапиро, который представил ее в статье, опубликованной в American Mathematical Monthly в 1999 году.

Недавно матрице Вейра было найдено несколько применений. Особый интерес представляет применение матрицы Вейра при изучении филогенетических инвариантов в биоматематике .

Определения

Определение

Базовая матрица Вейра с собственным значением $\lambda$ это $n\times n$ матрица $W$ следующего вида: Имеется целочисленный раздел

$n_{1}+n_{2}+\cdots +n_{r}=n$ из $n$ с $n_{1}\geq n_{2}\geq \cdots \geq n_{r}\geq 1$

такой, что, когда $W$ рассматривается как $r\times r$ блочная матрица $(W_{ij})$, где $(i,j)$ блокировать $W_{ij}$ это $n_{i}\times n_{j}$ матрицы присутствуют следующие три особенности:

1. Основные диагональные блоки $W_{ii}$ являются $n_{i}\times n_{i}$ скалярные матрицы $\lambda I$ для $i=1,\ldots ,r$.
2. Первые супердиагональные блоки $W_{i,i+1}$ являются полным рангом столбца $n_{i}\times n_{i+1}$ матрицы в сокращенной форме звеньев строк (т. е. единичная матрица, за которой следуют нулевые строки) для $i=1,\ldots ,r-1$.
3. Все остальные блоки W равны нулю (т.е. $W_{ij}=0$ когда $j\neq i,i+1$).

В этом случае мы говорим, что $W$ имеет структуру Вейра $(n_{1},n_{2},\ldots ,n_{r})$.

Пример

Ниже приведен пример базовой матрицы Вейра.

$W=$$={\begin{bmatrix}W_{11}&W_{12}&&\\&W_{22}&W_{23}&\\&&W_{33}&W_{34}\\&&&W_{44}\\\end{bmatrix}}$

В этой матрице $n=9$ и $n_{1}=4,n_{2}=2,n_{3}=2,n_{4}=1$. Так $W$ имеет структуру Вейра $(4,2,2,1)$. Также,

$W_{11}={\begin{bmatrix}\lambda &0&0&0\\0&\lambda &0&0\\0&0&\lambda &0\\0&0&0&\lambda \\\end{bmatrix}}=\lambda I_{4},\quad W_{22}={\begin{bmatrix}\lambda &0\\0&\lambda &\\\end{bmatrix}}=\lambda I_{2},\quad W_{33}={\begin{bmatrix}\lambda &0\\0&\lambda &\\\end{bmatrix}}=\lambda I_{2},\quad W_{44}={\begin{bmatrix}\lambda \\\end{bmatrix}}=\lambda I_{1}$

и

$W_{12}={\begin{bmatrix}1&0\\0&1\\0&0\\0&0\\\end{bmatrix}},\quad W_{23}={\begin{bmatrix}1&0\\0&1\\\end{bmatrix}},\quad W_{34}={\begin{bmatrix}1\\0\\\end{bmatrix}}.$

Определение

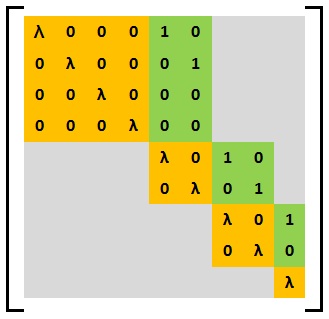
Позволять $W$ квадратная матрица и пусть $\lambda _{1},\ldots ,\lambda _{k}$ быть различными собственными значениями $W$. Мы говорим, что $W$ находится в форме Вейра (или является матрицей Вейра), если $W$ имеет следующую форму:

$W={\begin{bmatrix}W_{1}&&&\\&W_{2}&&\\&&\ddots &\\&&&W_{k}\\\end{bmatrix}}$

где $W_{i}$ представляет собой базовую матрицу Вейра с собственным значением $\lambda _{i}$ для $i=1,\ldots ,k$.

Пример

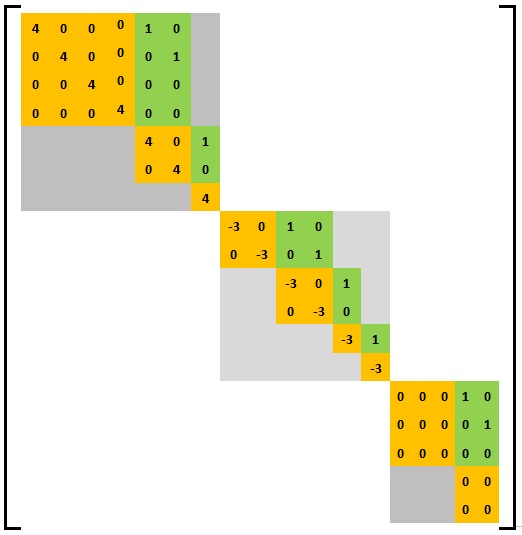
На следующем изображении показан пример общей матрицы Вейра, состоящей из трех основных блоков матрицы Вейра. Базовая матрица Вейра в верхнем левом углу имеет структуру (4,2,1) с собственным значением 4, средний блок имеет структуру (2,2,1,1) с собственным значением -3 и матрицу в правом нижнем углу. угол имеет структуру (3, 2) с собственным значением 0.

между Вейром и

Каноническая форма Вейра $W=P^{-1}JP$ связано с жордановой формой $J$ простой перестановкой $P$ для каждого базового блока Вейра следующим образом: Первый индекс каждого подблока Вейра образует самую большую цепь Иордана. После вычеркивания этих строк и столбцов первый индекс каждого нового подблока образует вторую по величине жордановую цепочку и так далее.

Форма Вейра канонична

То, что форма Вейра является канонической формой матрицы, является следствием следующего результата: Каждая квадратная матрица $A$ над алгебраически замкнутым полем аналогично матрице Вейра $W$ который уникален с точностью до перестановки его основных блоков. Матрица $W$ называется Вейрской (канонической) формой $A$.

Вейра

Приведение к нильпотентному случаю

Позволять $A$ быть квадратной матрицей порядка $n$ над алгебраически замкнутым полем и пусть различные собственные значения $A$ быть $\lambda _{1},\lambda _{2},\ldots ,\lambda _{k}$. Теорема о разложении Жордана – Шевалле утверждает, что $A$ аналогична вида блочно-диагональной матрице

$A={\begin{bmatrix}\lambda _{1}I+N_{1}&&&\\&\lambda _{2}I+N_{2}&&\\&&\ddots &\\&&&\lambda _{k}I+N_{k}\\\end{bmatrix}}={\begin{bmatrix}\lambda _{1}I&&&\\&\lambda _{2}I&&\\&&\ddots &\\&&&\lambda _{k}I\\\end{bmatrix}}+{\begin{bmatrix}N_{1}&&&\\&N_{2}&&\\&&\ddots &\\&&&N_{k}\\\end{bmatrix}}=D+N$

где $D$ матрица диагональная , $N$ является нильпотентной матрицей и $[D,N]=0$, оправдывая сокращение $N$ на подблоки $N_{i}$. Итак, проблема сокращения $A$ к форме Вейра сводится к проблеме приведения нильпотентных матриц $N_{i}$ в форму Вейра. Это приводит к обобщенной теореме о разложении в собственном пространстве .

Приведение нильпотентной матрицы к форме Вейра

Учитывая нильпотентную квадратную матрицу $A$ порядка $n$ над алгебраически замкнутым полем $F$, следующий алгоритм создает обратимую матрицу $C$ и матрица Вейра $W$ такой, что $W=C^{-1}AC$.

Шаг 1

Позволять $A_{1}=A$

Шаг 2

1. Вычислить основу для нулевого пространства $A_{1}$.
2. Расширить базис для нулевого пространства $A_{1}$ в основу для $n$-мерное векторное пространство $F^{n}$.
3. Формируем матрицу $P_{1}$ состоящее из этих базисных векторов.
4. Вычислить $P_{1}^{-1}A_{1}P_{1}={\begin{bmatrix}0&B_{2}\\0&A_{2}\end{bmatrix}}$. $A_{2}$ представляет собой квадратную матрицу размера $n$ − ничтожность $(A_{1})$.

Шаг 3

Если $A_{2}$ не равно нулю, повторите шаг 2 $A_{2}$.

1. Вычислить основу для нулевого пространства $A_{2}$.
2. Расширить базис для нулевого пространства $A_{2}$ к основе векторного пространства, имеющего размерность $n$ − ничтожность $(A_{1})$.
3. Формируем матрицу $P_{2}$ состоящее из этих базисных векторов.
4. Вычислить $P_{2}^{-1}A_{2}P_{2}={\begin{bmatrix}0&B_{3}\\0&A_{3}\end{bmatrix}}$. $A_{2}$ представляет собой квадратную матрицу размера $n$ − ничтожность $(A_{1})$ − ничтожность $(A_{2})$.

Шаг 4

Продолжайте процессы шагов 1 и 2, чтобы получить все более меньшие квадратные матрицы. $A_{1},A_{2},A_{3},\ldots$ и связанные с ними обратимые матрицы $P_{1},P_{2},P_{3},\ldots$ до первой нулевой матрицы $A_{r}$ получается.

Шаг 5

Структура Вейра $A$ является $(n_{1},n_{2},\ldots ,n_{r})$ где $n_{i}$ = недействительность $(A_{i})$.

Шаг 6

1. Вычислить матрицу $P=P_{1}{\begin{bmatrix}I&0\\0&P_{2}\end{bmatrix}}{\begin{bmatrix}I&0\\0&P_{3}\end{bmatrix}}\cdots {\begin{bmatrix}I&0\\0&P_{r}\end{bmatrix}}$ (здесь $I$- это единичные матрицы соответствующего размера).
2. Вычислить $X=P^{-1}AP$. $X$ представляет собой матрицу следующего вида:

$X={\begin{bmatrix}0&X_{12}&X_{13}&\cdots &X_{1,r-1}&X_{1r}\\&0&X_{23}&\cdots &X_{2,r-1}&X_{2r}\\&&&\ddots &\\&&&\cdots &0&X_{r-1,r}\\&&&&&0\end{bmatrix}}$.

Шаг 7

Используйте элементарные операции над строками, чтобы найти обратимую матрицу. $Y_{r-1}$ подходящего размера, чтобы изделие $Y_{r-1}X_{r,r-1}$ представляет собой матрицу вида $I_{r,r-1}={\begin{bmatrix}I\\O\end{bmatrix}}$.

Шаг 8

Набор $Q_{1}=$ Диагностика $(I,I,\ldots ,Y_{r-1}^{-1},I)$ и вычислить $Q_{1}^{-1}XQ_{1}$. В этой матрице $(r,r-1)$-блок это $I_{r,r-1}$.

Шаг 9

Найти матрицу $R_{1}$ формируется как произведение элементарных матриц таких, что $R_{1}^{-1}Q_{1}^{-1}XQ_{1}R_{1}$ представляет собой матрицу, в которой все блоки над блоком $I_{r,r-1}$ содержать только $0$х.

Шаг 10

Повторите шаги 8 и 9 для столбца. $r-1$ преобразование $(r-1,r-2)$-блокировать $I_{r-1,r-2}$ посредством сопряжения некоторой обратимой матрицей $Q_{2}$. Используйте этот блок, чтобы очистить блоки выше, путем спряжения продуктом. $R_{2}$ элементарных матриц.

Шаг 11

Повторите эти процессы на $r-2,r-3,\ldots ,3,2$ столбцы, используя спряжения по $Q_{3},R_{3},\ldots ,Q_{r-2},R_{r-2},Q_{r-1}$. Полученная матрица $W$ теперь находится в форме Вейра.

Шаг 12

Позволять $C=P_{1}{\text{diag}}(I,P_{2})\cdots {\text{diag}}(I,P_{r-1})Q_{1}R_{1}Q_{2}\cdots R_{r-2}Q_{r-1}$. Затем $W=C^{-1}AC$.

Приложения формы Вейра

Некоторые известные применения формы Weyr перечислены ниже:

1. Форму Вейра можно использовать для упрощения доказательства теоремы Герстенхабера, утверждающей, что подалгебра, порожденная двумя коммутирующими $n\times n$ матрицы имеют не более чем размерность $n$.
2. Множество конечных матриц называется приблизительно одновременно диагонализируемым, если их можно преобразовать в одновременно диагонализируемые матрицы. Форма Вейра используется для доказательства приближенной одновременной диагонализуемости различных классов матриц. Свойство приближенной одновременной диагонализуемости находит применение при изучении филогенетических инвариантов в биоматематике .
3. Форму Вейра можно использовать для упрощения доказательства неприводимости многообразия всех k -кортежей коммутирующих комплексных матриц.