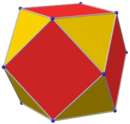
Архимедово тело

Усеченный тетраэдр , кубооктаэдр и усеченный икосододекаэдр . Первое можно назвать наименьшим архимедовым телом, а последнее — самым большим.

Ромбокубооктаэдр и псевдоромбокубооктаэдр.

В геометрии архимедово тело — это один из 13 выпуклых многогранников , грани которых представляют собой правильные многоугольники , а вершины симметричны друг другу. Впервые их перечислил Архимед . Они принадлежат к классу выпуклых однородных многогранников , выпуклых многогранников с правильными гранями и симметричными вершинами, который делится на архимедовы тела, пять платоновых тел (каждое имеет только один тип многоугольной грани) и два бесконечных семейства призм. и антипризмы . Псевдоморомбикубооктаэдр — это дополнительный многогранник с правильными гранями и конгруэнтными вершинами, но его обычно не считают архимедовым телом, поскольку он не является вершинно-транзитивным . Еще больший класс, чем выпуклые однородные многогранники, — это тела Джонсона , чьи правильные многоугольные грани не обязательно должны встречаться в одинаковых вершинах.

В этих многогранниках вершины идентичны в том смысле, что глобальная изометрия всего тела переводит любую вершину в любую другую. Бранко Грюнбаум ( 2009 ) заметил, что 14-й многогранник, вытянутый квадратный гиробикупола (или псевдоромбокубооктаэдр), соответствует более слабому определению архимедова тела, в котором «идентичные вершины» означаютпросто части многогранника вблизи любых двух вершин выглядят одинаково (они имеют одинаковую форму граней, сходящихся вокруг каждой вершины в одинаковом порядке и образующих одинаковые углы). Грюнбаум указал на частую ошибку, когда авторы определяют архимедовы тела, используя некоторую форму этого локального определения, но опускают 14-й многогранник. Если необходимо указать только 13 многогранников, в определении должна использоваться глобальная симметрия многогранника, а не локальные окрестности.

Призмы и антипризмы , группами симметрии которых являются группы диэдра , обычно не считаются архимедовыми телами, хотя их грани представляют собой правильные многоугольники, а их группы симметрии действуют транзитивно на их вершинах. За исключением этих двух бесконечных семейств, существует 13 архимедовых тел. Все архимедовы тела (кроме вытянутого квадратного гиробикупола) могут быть построены с помощью конструкций Витгофа из платоновых тел с тетраэдрической , октаэдрической и икосаэдрической симметрией .

Происхождение имени

Архимедовы тела получили свое название от Архимеда , который обсуждал их в ныне утерянной работе. Папп ссылается на него, утверждая, что Архимед перечислил 13 многогранников. и математики ценили В эпоху Возрождения художники чистые формы с высокой симметрией, и примерно к 1620 году Иоганн Кеплер завершил повторное открытие 13 многогранников. а также определение призм , антипризм и невыпуклых тел, известных как многогранники Кеплера-Пуансо . ( в Schreiber, Fischer & Sternath, 2008. Дополнительную информацию о повторном открытии архимедовых тел в эпоху Возрождения см. )

Кеплер, возможно, также нашел вытянутый квадратный гиробикупол (псевдоромбокубооктаэдр): по крайней мере, он однажды заявил, что существует 14 архимедовых тел. Однако его опубликованное перечисление включает только 13 однородных многогранников, а первое четкое заявление о существовании псевдоромбокубооктаэдра было сделано в 1905 году Дунканом Соммервиллем .

Классификация

Всего существует 13 архимедовых тел (не считая вытянутого квадратного гиробикупола ; 15, если зеркальные изображения двух энантиоморфов считать отдельно — курносого куба и курносого додекаэдра).

Здесь конфигурация вершин относится к типу правильных многоугольников, которые встречаются в любой заданной вершине. Например, конфигурация вершин 4.6.8 означает, что квадрат , шестиугольник и восьмиугольник встречаются в вершине (при этом порядок вокруг вершины принимается по часовой стрелке).

Имя/ (альтернативное название)	Шлефли Коксетер	Прозрачный	Твердый	Сеть	Вертекс конф. / инжир.	Лица		Края	Зеленый.	Объем (края единицы)	Точка группа	Сферичность
Усеченный тетраэдр	т{3,3}				3.6.6	8	4 треугольника 4 шестиугольника	18	12	2.710 576	Т д	0.775 4132
Кубооктаэдр (ромбитетратраэдр, треугольный гиробикупол)	г{4,3} или рр{3,3} или				3.4.3.4	14	8 треугольников 6 квадратов	24	12	2.357 023	Ой ​	0.904 9972
Усеченный куб	т{4,3}				3.8.8	14	8 треугольников 6 восьмиугольников	36	24	13.599 663	Ой ​	0.849 4937
Усеченный октаэдр (усеченный тетратетраэдр)	т{3,4} или тр{3,3} или				4.6.6	14	6 квадратов 8 шестиугольников	36	24	11.313 709	Ой ​	0.909 9178
Ромбокубооктаэдр (маленький ромбокубооктаэдр, вытянутый квадратный ортобикупол)	рр{4,3}				3.4.4.4	26	8 треугольников 18 квадратов	48	24	8.714 045	Ой ​	0.954 0796
Усеченный кубооктаэдр (большой ромбокубооктаэдр)	тр{4,3}				4.6.8	26	12 квадратов 8 шестиугольников 6 восьмиугольников	72	48	41.798 990	Ой ​	0.943 1657
Курносый куб ( курносый кубооктаэдр )	ср{4,3}				3.3.3.3.4	38	32 треугольника 6 квадратов	60	24	7.889 295	ТО	0.965 1814
Икосододекаэдр (пятиугольная гиробиротунда)	г{5,3}				3.5.3.5	32	20 треугольников 12 пятиугольников	60	30	13.835 526	I h	0.951 0243
Усеченный додекаэдр	т{5,3}				3.10.10	32	20 треугольников 12 декагонов	90	60	85.039 665	I h	0.926 0125
Усеченный икосаэдр	т{3,5}				5.6.6	32	12 пятиугольников 20 шестиугольников	90	60	55.287 731	I h	0.966 6219
Ромбикосидодекаэдр (маленький ромбокосододекаэдр)	рр{5,3}				3.4.5.4	62	20 треугольников 30 квадратов 12 пятиугольников	120	60	41.615 324	I h	0.979 2370
Усеченный икосододекаэдр (большой ромбокосододекаэдр)	тр{5,3}				4.6.10	62	30 квадратов 20 шестиугольников 12 декагонов	180	120	206.803 399	I h	0.970 3127
Курносый додекаэдр ( курносый икосододекаэдр )	ср{5,3}				3.3.3.3.5	92	80 треугольников 12 пятиугольников	150	60	37.616 650	я	0.982 0114

Некоторые определения полуправильного многогранника включают еще одну фигуру — вытянутый квадратный гиробикупол или «псевдоромбокубооктаэдр».

Характеристики

Число вершин равно 720°, делённому на дефект угла вершины .

Кубооктаэдр и икосододекаэдр однородны по ребрам и называются квазиправильными .

Двойники телами архимедовых тел называются каталонскими . Вместе с бипирамидами и трапецоэдрами это гранеоднородные тела с правильными вершинами.

Хиральность

Курносый куб и курносый додекаэдр известны как хиральные , поскольку они бывают левосторонней формы (лат. levomorph или laevomorph) и правосторонней формы (лат. dextromorph). Когда что-то существует в нескольких формах, которые являются трехмерным зеркальным отражением друг друга , эти формы можно назвать энантиоморфами. (Эта номенклатура используется также для форм некоторых химических соединений .)

Построение архимедовых тел

Дополнительная информация: Однородный многогранник и обозначение многогранника Конвея.

Архимедовы тела можно построить как образующие позиции в калейдоскопе .

Различные архимедовы и платоновы тела можно связать друг с другом с помощью нескольких общих конструкций. Начиная с платонова тела, усечение включает в себя срезание углов. Для сохранения симметрии разрез производится в плоскости, перпендикулярной линии, соединяющей угол с центром многогранника, и одинаков для всех углов. В зависимости от того, насколько усечено (см. таблицу ниже), могут быть созданы разные Платоновы, Архимедовы (и другие) тела. Если усечение достаточно глубокое, так что каждая пара граней соседних вершин имеет ровно одну общую точку, это называется выпрямлением. Расширение предполагает перемещение каждой грани от центра (на одинаковое расстояние , или кантелляция чтобы сохранить симметрию Платонова тела) и взятие выпуклой оболочки. Расширение со скручиванием также предполагает вращение граней, при этом каждый прямоугольник, соответствующий ребру, разбивается на два треугольника по одной из диагоналей прямоугольника. Последняя конструкция, которую мы здесь используем, — это усечение как углов, так и ребер. Игнорируя масштабирование, расширение также можно рассматривать как исправление исправления. Подобным же образом канти-усечение можно рассматривать как усечение исправления.

Построение архимедовых тел

Симметрия		Тетраэдрический	Октаэдрический		икосаэдрический
Начало твердое Операция	Символ {п, д}	Тетраэдр {3,3}	Куб {4,3}	Октаэдр {3,4}	Додекаэдр {5,3}	Икосаэдр {3,5}
Усечение (т)	t{p,q}	усеченный тетраэдр	усеченный куб	усеченный октаэдр	усеченный додекаэдр	усеченный икосаэдр
Исправление (р) Выше (а)	г {р, q}	тетратетраэдр (октаэдр)	кубооктаэдр		икосододекаэдр
Биусечение (2t) Двойной кис (дк)	2t{p,q}	усеченный тетраэдр	усеченный октаэдр	усеченный куб	усеченный икосаэдр	усеченный додекаэдр
Биректификация (2r) Двойной (д)	2r{p,q}	тетраэдр	октаэдр	куб	икосаэдр	додекаэдр
Кантелляция (rr) Расширение (е)	rr{p,q}	ромбитетратраэдр (кубооктаэдр)	ромбокубооктаэдр		ромбикосидодекаэдр
Курносый исправлен (ср) Курносый (с)	ср{п,q}	курносый тетратетраэдр (икосаэдр)	курносый кубооктаэдр		курносый икосододекаэдр
Усечение количества (tr) Фаска (б)	tr{p,q}	усеченный тетратетраэдр (усеченный октаэдр)	усеченный кубооктаэдр		усеченный икосододекаэдр

Обратите внимание на двойственность куба и октаэдра, а также додекаэдра и икосаэдра. Кроме того, отчасти потому, что тетраэдр самодуален, только одно архимедово тело имеет не более чем тетраэдрическую симметрию. (Все Платоновы тела обладают, по крайней мере, тетраэдрической симметрией, поскольку тетраэдрическая симметрия — это операция симметрии (т. е. включена в) октаэдрической и изоэдрической симметрии, что демонстрируется тем фактом, что октаэдр можно рассматривать как выпрямленный тетраэдр, а икосаэдр можно рассматривать как выпрямленный тетраэдр. можно использовать как курносый тетраэдр.)

Стереографическая проекция

усеченный тетраэдр		усеченный куб		усеченный октаэдр		усеченный додекаэдр		усеченный икосаэдр
треугольник с центром	шестиугольник с центром	восьмиугольник с центром	треугольник с центром	квадратно -центрированный	шестиугольник с центром	Декагон -центрированный	Треугольник -центрированный	пятиугольник в центре	шестиугольник с центром

кубооктаэдр			икосододекаэдр		ромбокубооктаэдр			ромбикосидодекаэдр
квадратно -центрированный	треугольник с центром	вершинно -центрированный	пятиугольник в центре	треугольник с центром	квадратно -центрированный	квадратно -центрированный	треугольник с центром	Пятиугольник в центре	Треугольник -центрированный	Квадрат -центрированный

усеченный кубооктаэдр			усеченный икосододекаэдр			курносый куб
квадратно -центрированный	шестиугольник с центром	восьмиугольник с центром	десятиугольник -центрированный	шестиугольник с центром	квадратно -центрированный	квадратно -центрированный

См. также

• Апериодическое замощение
• Архимедов график
• Икосаэдрические близнецы
• Список однородных многогранников
• Куб принца Руперта#Обобщения
• Квазикристалл
• Правильный многогранник
• Полуправильный многогранник
• Тороидальный многогранник
• Однородный многогранник

Цитаты

Цитируемые работы

• Грюнбаум, Бранко (2009), «Непреходящая ошибка», Elemente der Mathematik , 64 (3): 89–101, doi : 10.4171/EM/120 , MR   2520469 . Перепечатано в Питичи, Мирча, изд. (2011), Лучшие статьи по математике 2010 г. , Princeton University Press, стр. 18–31 .
• Малкевич, Джозеф (1988), «Вехи в истории многогранников», в Сенечале, М .; Флек, Г. (ред.), Формирование пространства: многогранный подход , Бостон: Биркхойзер, стр. 80–92 .

Общие ссылки

• Джаятилаке, Удая (март 2005 г.). «Расчеты на гранях и вершинах правильных многогранников». Математический вестник . 89 (514): 76–81. дои : 10.1017/S0025557200176818 . S2CID   125675814 . .
• Пью, Энтони (1976). Многогранники: визуальный подход . Калифорния: Издательство Калифорнийского университета в Беркли. ISBN  0-520-03056-7 . Глава 2
• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN  0-486-23729-Х . (Раздел 3–9)
• Шрайбер, Питер; Фишер, Гизела; Стернат, Мария Луиза (2008). «Новый взгляд на повторное открытие архимедовых тел в эпоху Возрождения». Архив истории точных наук . 62 (4): 457–467. Бибкод : 2008AHES...62..457S . дои : 10.1007/s00407-008-0024-z . ISSN   0003-9519 . S2CID   122216140 . .

Внешние ссылки

• Вайсштейн, Эрик В. «Архимедово тело» . Математический мир .
• Архимедовы тела Эрика В. Вайсштейна , Демонстрационный проект Wolfram .
• Бумажные модели Архимедовых тел и Каталанских тел
• Бесплатные бумажные модели(сетки) архимедовых тел
• Равномерные многогранники доктора Р. Мэдера
• Архимедовы тела и визуальные многогранники Дэвида И. МакКуи
• Многогранники виртуальной реальности , Энциклопедия многогранников Джорджа Харта
• Предпоследнее модульное оригами Джеймса С. Планка
• Интерактивные 3D-многогранники на Java
• Solid Body Viewer — это интерактивный просмотрщик 3D-многогранников, который позволяет сохранять модель в формате svg, stl или obj.
• Stella: Polyhedron Navigator : программное обеспечение, использованное для создания многих изображений на этой странице.
• Бумажные модели архимедовых (и других) многогранников